Презентация на тему: Осевая симметрия 8 класс

Осевая симметрия Геометрия8 класс

Цели урока Ввести понятие точек и фигур, симметричных относительно прямой Научить строить симметричные точки и распознавать фигуры, обладающие осевой симметрией

План урока Организационный моментПроверка домашнего задания (Тест)Изучение новой темы 4. Закрепление нового материалаПодведение итоговДомашнее задание6. Фотоальбом (Практическое применение осевой симметрии)

Содержание Тест по теме: «Четырёхугольники» Осевая симметрияЗанимательные задачи Практическая работа Вопросы по теме: «Осевая симметрия» Домашнее задание Фотоальбом (Практическое применение осевой симметрии)

Осевая симметрия Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Осевая симметрия Фигура называется симметричной относительно прямой а, если для каждой точки фигуры, симметричная ей точка относительно прямой а также принадлежит этой фигуре. а - ось симметрии
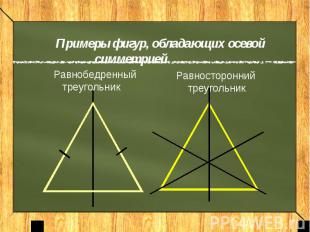
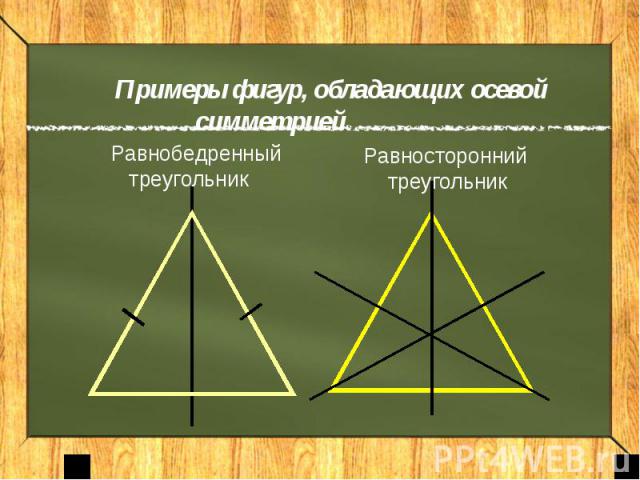
Примеры фигур, обладающих осевой симметрией Равнобедренный треугольникРавносторонний треугольник
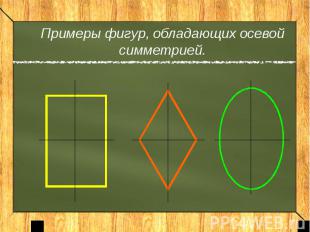
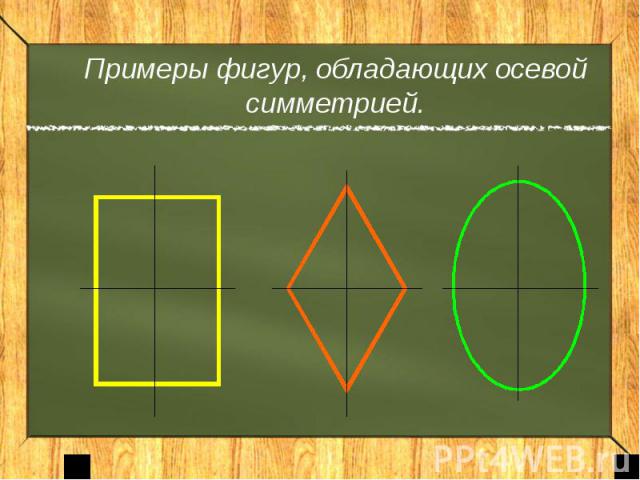
Примеры фигур, обладающих осевой симметрией.

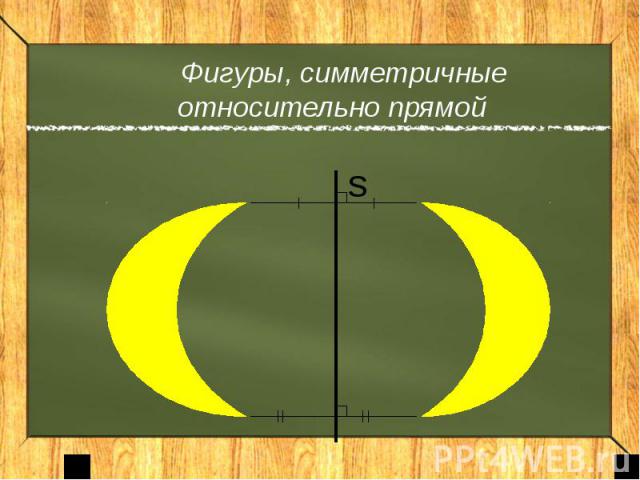
Фигуры, симметричные относительно прямой

Сколько осей симметрии имеют данные фигуры?

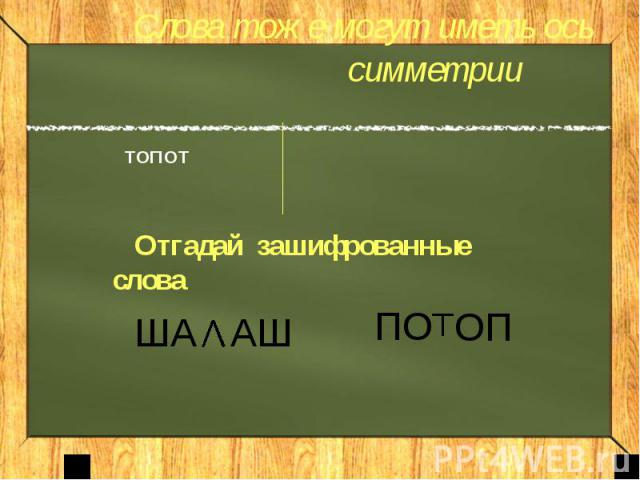
Отгадайте зашифрованные слова

Слова тоже могут иметь ось симметрии Отгадай зашифрованные слова

Какая из фигур лишняя?

Задание 1 Известно, что точки Е и F симметричны относительно прямой m. Постройте прямую m.

Проверь себя

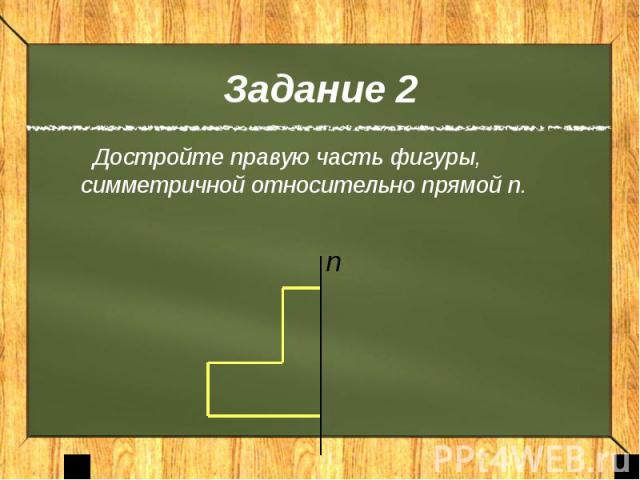
Задание 2 Достройте правую часть фигуры, симметричной относительно прямой n.
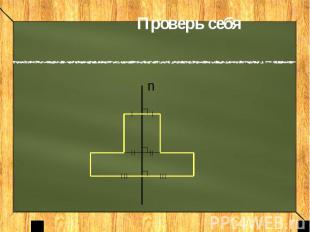
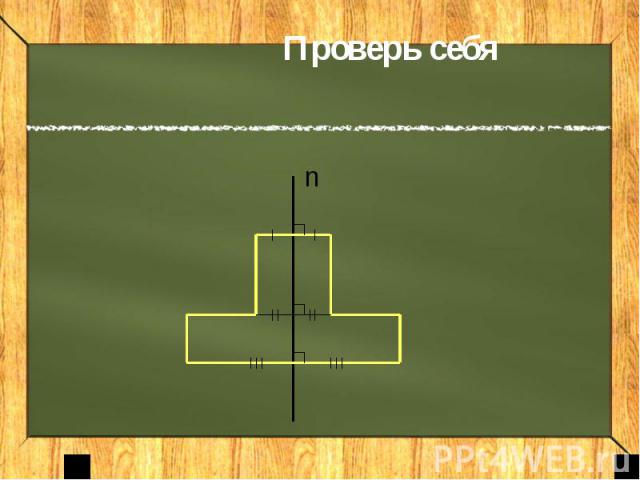
Проверь себя
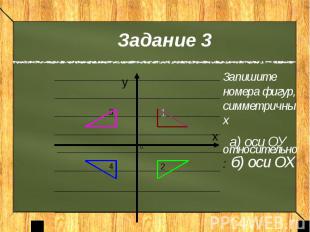
Задание 3 Запишите номера фигур, симметричных относительно:

Ответь на вопросы 1. Дайте определение точек, симметричных относительно прямой. 2. Фигуры, симметричной относительно прямой. 3. Приведите примеры использования осевой симметрии в жизни.