Презентация на тему: Новые признаки равенства треугольников

Школьное научное общество школы №1131 Новые признаки равенства треугольников Автор: Жабин Виктор, Бобков Сергей. Научный руководитель: Кузнецова Т. Н. 2004 г. г. Москва

Содержание:

ВВЕДЕНИЕ

В курсе геометрии 7 класса изучаются 3 признака равенства треугольников, которые позволяют решать определённый тип задач. Мы решили расширить теоретическую базу по признакам равенства треугольников, добавив к сторонам и углам, используемым в классических признаках равенства треугольников, другие компоненты: биссектрису, медиану и высоту. В курсе геометрии 7 класса изучаются 3 признака равенства треугольников, которые позволяют решать определённый тип задач. Мы решили расширить теоретическую базу по признакам равенства треугольников, добавив к сторонам и углам, используемым в классических признаках равенства треугольников, другие компоненты: биссектрису, медиану и высоту. Таким образом, целями нашей работы является: 1. Сформулировать новые признаки равенства треугольников, используя понятия: биссектрисы, медианы и высоты. 2. Доказать новые признаки равенства треугольников. 3. Продемонстрировать другим учащимся существование в математике «белых пятен» и возможности их доказательства.

ТЕОРИЯ

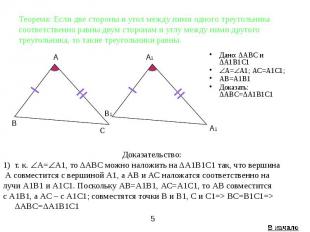
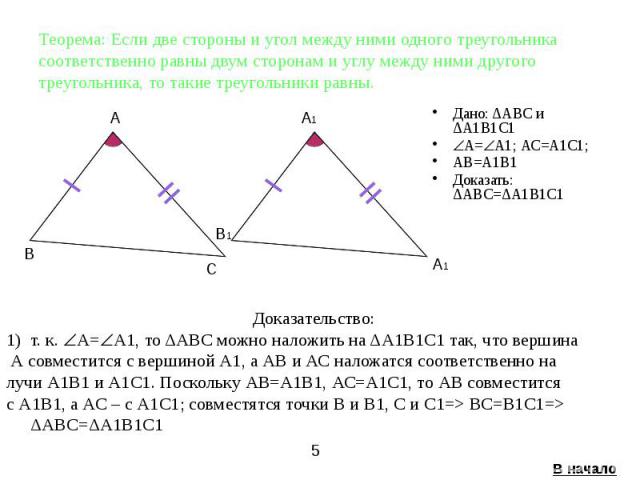
Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 А= А1; АС=А1С1; AВ=А1В1 Доказать: ΔАВС=ΔА1В1С1

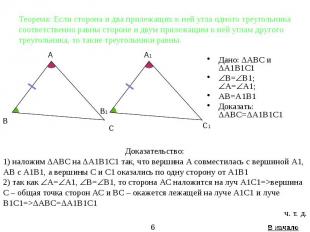
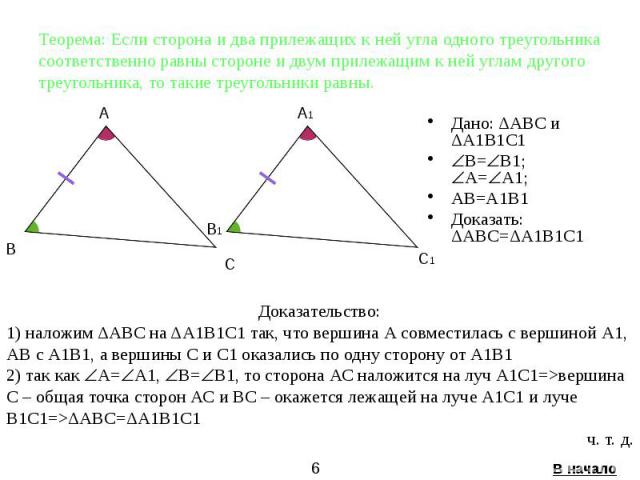
Теорема: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 B= B1; А= А1; AВ=A1В1 Доказать: ΔАВС=ΔА1В1С1

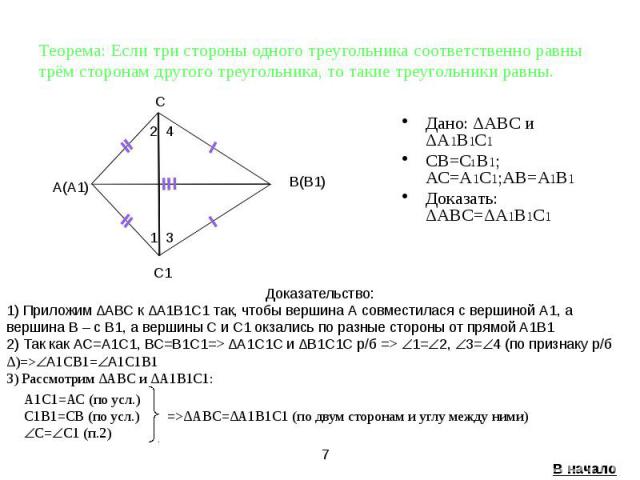
Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 СВ=С1В1; АС=А1С1;AВ=А1В1 Доказать: ΔАВС=ΔА1В1С1

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ СВЯЗАННЫЕ С ВЫСОТОЙ 8

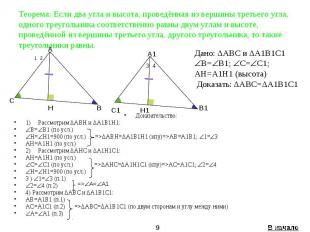
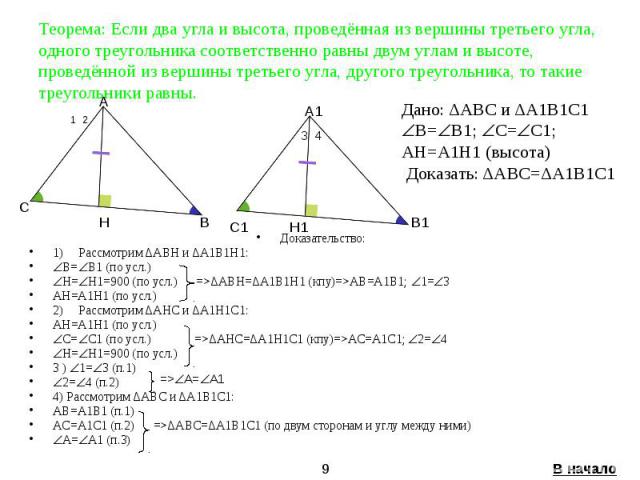
Теорема: Если два угла и высота, проведённая из вершины третьего угла, одного треугольника соответственно равны двум углам и высоте, проведённой из вершины третьего угла, другого треугольника, то такие треугольники равны. Доказательство: 1) Рассмотрим ΔABH и ΔA1B1H1: B= B1 (по усл.) H= H1=900 (по усл.) =>ΔABH=ΔA1B1H1 (кпу)=>AB=A1B1; 1= 3 AH=A1H1 (по усл.) 2) Рассмотрим ΔAHC и ΔA1H1C1: AH=A1H1 (по усл.) C= C1 (по усл.) =>ΔAHC=ΔA1H1C1 (кпу)=>AC=A1C1; 2= 4 H= H1=900 (по усл.) 3 ) 1= 3 (п.1) 2= 4 (п.2) 4) Рассмотрим ΔABC и ΔA1B1C1: AB=A1B1 (п.1) AC=A1C1 (п.2) =>ΔABC=ΔA1B1C1 (по двум сторонам и углу между ними) A= A1 (п.3)

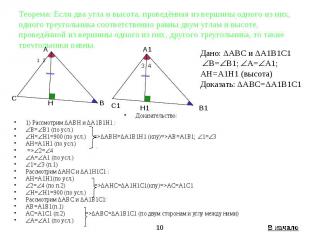
Теорема: Если два угла и высота, проведённая из вершины одного из них, одного треугольника соответственно равны двум углам и высоте, проведённой из вершины одного из них, другого треугольника, то такие треугольники равны. Доказательство: 1) Рассмотрим ΔABH и ΔA1B1H1 : B= B1 (по усл.) H= H1=900 (по усл.) =>ΔABH=ΔA1B1H1 (кпу)=>AB=A1B1; 1= 3 AH=A1H1 (по усл.) => 2= 4 A= A1 (по усл.) 1= 3 (п.1) Рассмотрим ΔAHC и ΔA1H1C1 : AH=A1H1(по усл.) 2= 4 (по п.2) =>ΔAHC=ΔA1H1C1(кпу)=>AC=A1C1 H= H1=900 (по усл.) Рассмотрим ΔABC и ΔA1B1C1: AB=A1B1(п.1) AC=A1C1 (п.2) =>ΔABC=ΔA1B1C1 (по двум сторонам и углу между ними) A= A1 (по усл.)

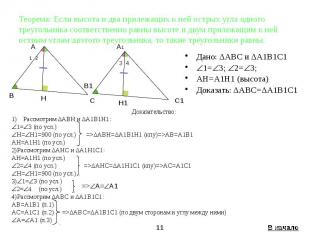
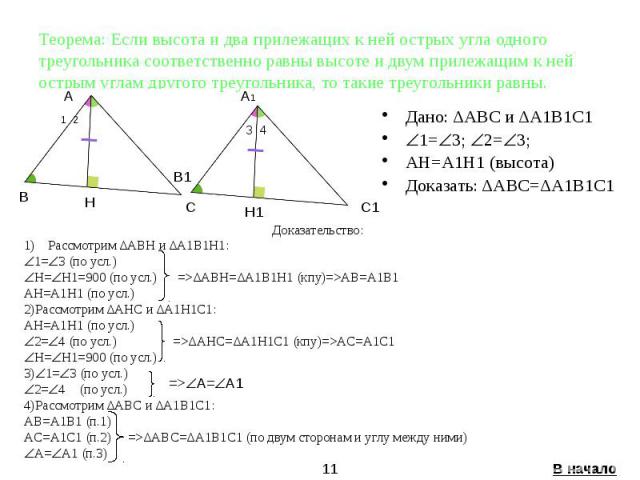
Теорема: Если высота и два прилежащих к ней острых угла одного треугольника соответственно равны высоте и двум прилежащим к ней острым углам другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 1= 3; 2= 3; AH=A1H1 (высота) Доказать: ΔАВС=ΔА1В1С1

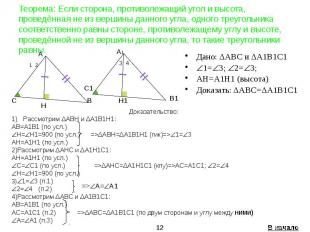
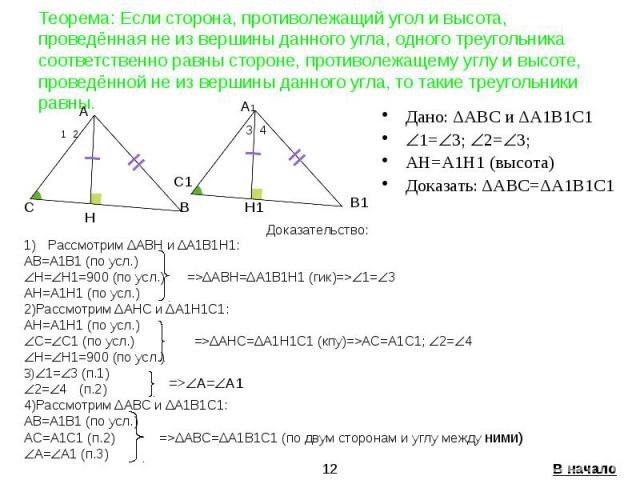
Теорема: Если сторона, противолежащий угол и высота, проведённая не из вершины данного угла, одного треугольника соответственно равны стороне, противолежащему углу и высоте, проведённой не из вершины данного угла, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 1= 3; 2= 3; AH=A1H1 (высота) Доказать: ΔАВС=ΔА1В1С1

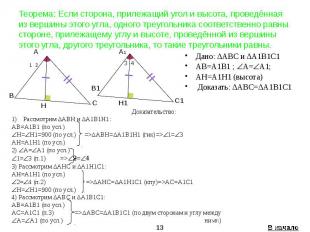
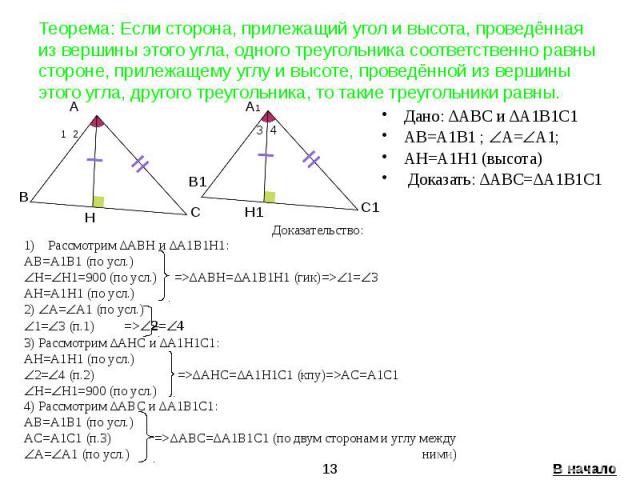
Теорема: Если сторона, прилежащий угол и высота, проведённая из вершины этого угла, одного треугольника соответственно равны стороне, прилежащему углу и высоте, проведённой из вершины этого угла, другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 AB=A1B1 ; А= А1; AH=A1H1 (высота) Доказать: ΔАВС=ΔА1В1С1

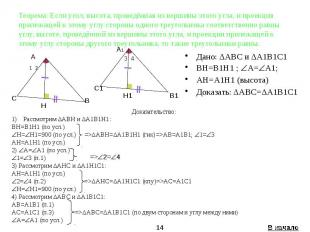
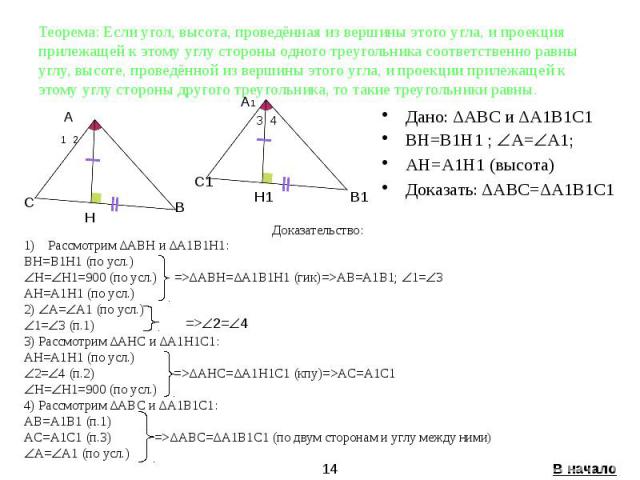
Теорема: Если угол, высота, проведённая из вершины этого угла, и проекция прилежащей к этому углу стороны одного треугольника соответственно равны углу, высоте, проведённой из вершины этого угла, и проекции прилежащей к этому углу стороны другого треугольника, то такие треугольники равны. Дано: ΔАВС и ΔА1В1С1 BH=B1H1 ; А= А1; AH=A1H1 (высота) Доказать: ΔАВС=ΔА1В1С1

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ СВЯЗАННЫЕ С БИССЕКТРИСОЙ

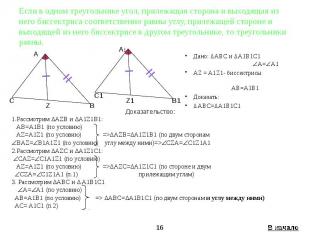
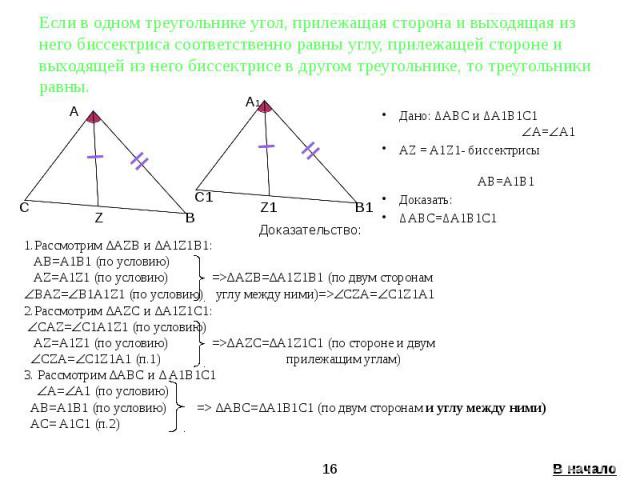
Если в одном треугольнике угол, прилежащая сторона и выходящая из него биссектриса соответственно равны углу, прилежащей стороне и выходящей из него биссектрисе в другом треугольнике, то треугольники равны. Дано: ∆ABC и ∆A1B1C1 A= A1 AZ = A1Z1- биссектрисы AB=A1B1 Доказать: ∆ABC=∆A1B1C1

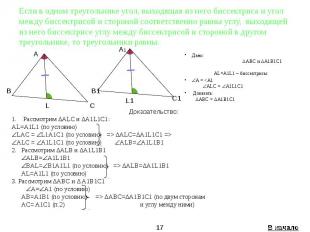
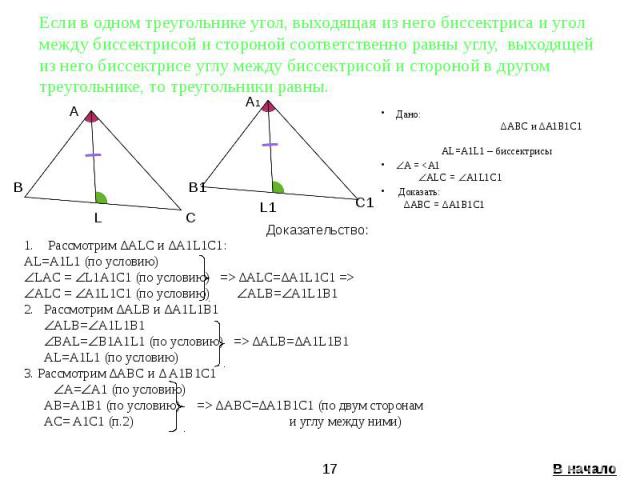
Если в одном треугольнике угол, выходящая из него биссектриса и угол между биссектрисой и стороной соответственно равны углу, выходящей из него биссектрисе углу между биссектрисой и стороной в другом треугольнике, то треугольники равны. Дано: ∆ABC и ∆A1B1C1 AL=A1L1 – биссектрисы A = <A1 ALC = A1L1C1 Доказать: ∆ABC = ∆A1B1C1

ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ СВЯЗАННЫЕ С МЕДИАНОЙ

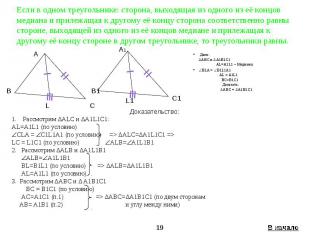
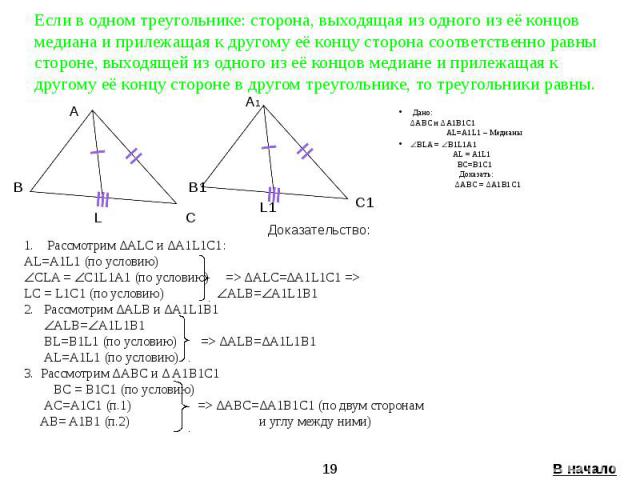
Если в одном треугольнике: сторона, выходящая из одного из её концов медиана и прилежащая к другому её концу сторона соответственно равны стороне, выходящей из одного из её концов медиане и прилежащая к другому её концу стороне в другом треугольнике, то треугольники равны. Дано: ∆ABC и ∆A1B1C1 AL=A1L1 – Медианы BLA = B1L1A1 AL = A1L1 BC=B1C1 Доказать: ∆ABC = ∆A1B1C1

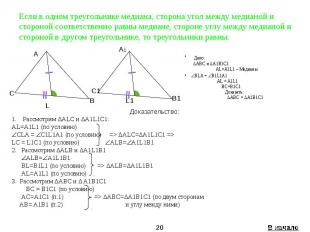
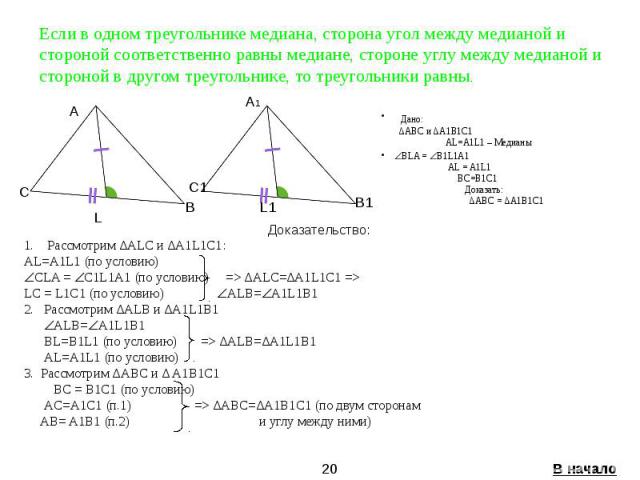
Если в одном треугольнике медиана, сторона угол между медианой и стороной соответственно равны медиане, стороне углу между медианой и стороной в другом треугольнике, то треугольники равны. Дано: ∆ABC и ∆A1B1C1 AL=A1L1 – Медианы BLA = B1L1A1 AL = A1L1 BC=B1C1 Доказать: ∆ABC = ∆A1B1C1

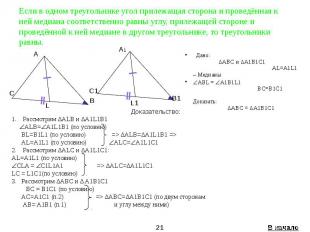
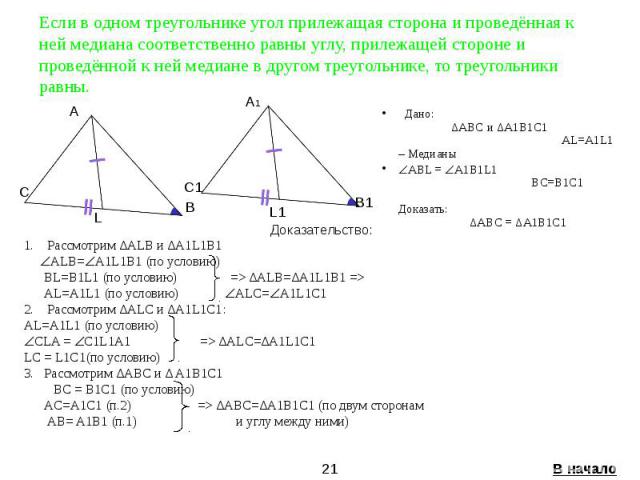
Если в одном треугольнике угол прилежащая сторона и проведённая к ней медиана соответственно равны углу, прилежащей стороне и проведённой к ней медиане в другом треугольнике, то треугольники равны. Дано: ∆ABC и ∆A1B1C1 AL=A1L1 – Медианы ABL = A1B1L1 BC=B1C1 Доказать: ∆ABC = ∆A1B1C1

ЛИТЕРАТУРА

1. Геометрия 7-9 кл. Авторы: Л. С. Атанасян, В. Ф. Бутузов.

РЕЦЕНЗИЯ