Презентация на тему: Метод вспомогательной окружности

Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он также неисчерпаем, как и Вселенная. Окружность - душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите свою» Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он также неисчерпаем, как и Вселенная. Окружность - душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите свою»

Существует причина, по которой мы решили выбрать для исследовательской работы тему: «Метод вспомогательной окружности». На следующий год нам предстоит сдать экзамены, а материал, который дается в наших учебниках не достаточен. Существует причина, по которой мы решили выбрать для исследовательской работы тему: «Метод вспомогательной окружности». На следующий год нам предстоит сдать экзамены, а материал, который дается в наших учебниках не достаточен. Более глубокое изучение различных методов дополнительных построений, может привести к ответу более коротким путем.

Гипотеза: если изучить методы дополнительных построений, в частности метод вспомогательной окружности, то это будет способствовать более успешному решению задач в курсе геометрии и на ЕГЭ по математике. Гипотеза: если изучить методы дополнительных построений, в частности метод вспомогательной окружности, то это будет способствовать более успешному решению задач в курсе геометрии и на ЕГЭ по математике.   Цель: Приобретение знаний и умений по применению метода вспомогательной окружности. Для решения поставленной проблемы и проверки сформулированной гипотезы необходимо было решить следующие задачи: 1. Определить виды различных дополнительных построений, особенности их реализации; установить место и значение задач, решаемых с помощью дополнительных построений,. 2. Изучить существующий метод вспомогательной окружности. 3. Определить теоретическую базу, необходимую для реализации данного метода. 4. Выявить требования к наборам задач по их признакам, методику работы с ними. 5. Осуществить экспериментальную проверку разработанной методики.  

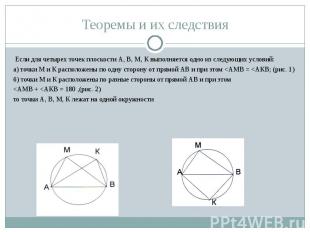
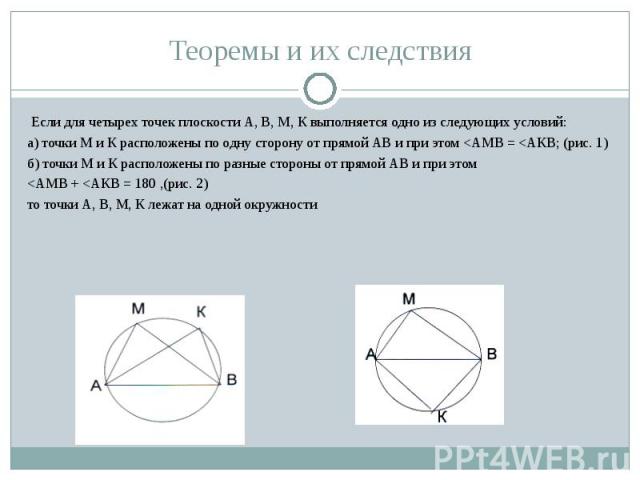
 Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:  Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий: а) точки М и К расположены по одну сторону от прямой АВ и при этом <АМВ = <АКВ; (рис. 1) б) точки М и К расположены по разные стороны от прямой АВ и при этом <АМВ + <АКВ = 180 ,(рис. 2) то точки А, В, М, К лежат на одной окружности

1.Если дан правильный треугольник, то можно провести окружность с центром в любой из его вершин и радиусом, равным длине его стороны, либо описать около него окружность, которая разобьется вершинами треугольника на равные дуги по 1200 каждая. 2.Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы, а радиус равен медиане, проведенной к гипотенузе этого треугольника. 3.Если удается установить, что суммы противоположных углов выпуклого четырехугольника равны, то вокруг него описывается окружность.

4.Если дан квадрат, прямоугольник или равнобедренная трапеция, то вокруг них описывается окружность. 4.Если дан квадрат, прямоугольник или равнобедренная трапеция, то вокруг них описывается окружность. 5.Если для четырех точек плоскости А, В, К и М выполняется условие: точки М и К расположены по одну сторону от прямой АВ и при этом ∟АМВ = ∟АКВ, то точки А, В, М и К лежат на одной окружности (Заметим, что если ∟АМВ = ∟АКВ = 900, то точки А, В, М и К расположены на окружности с диаметром АВ. ). 6.Если в треугольнике заданы биссектриса и медиана или биссектриса и серединный перпендикуляр, проведенные к одной и той же стороне, то около треугольника описывается окружность, а биссектриса продолжается до пересечения с нею. Продолжение биссектрисы и серединный перпендикуляр, проходящий через основание медианы, встретятся в середине дуги, стягиваемой стороной, к которой они проведены.

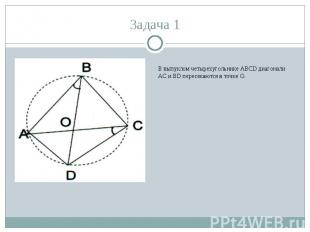
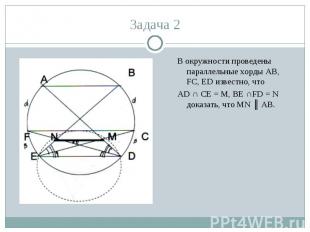
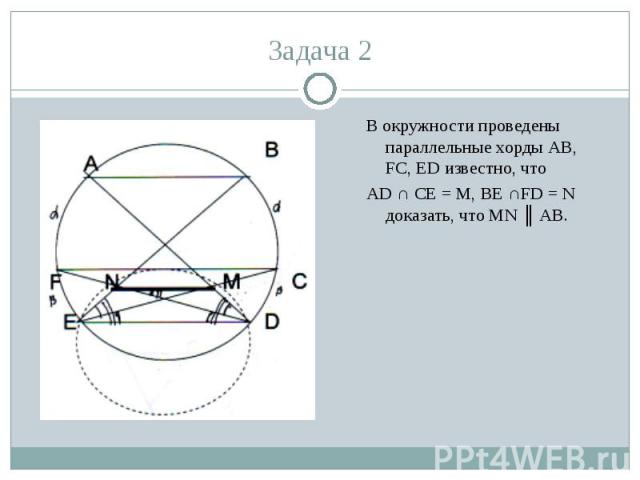
В окружности проведены параллельные хорды АВ, FC, ED известно, что В окружности проведены параллельные хорды АВ, FC, ED известно, что AD ∩ CE = M, BE ∩FD = N доказать, что МN ║ АВ.

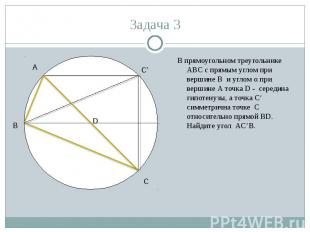
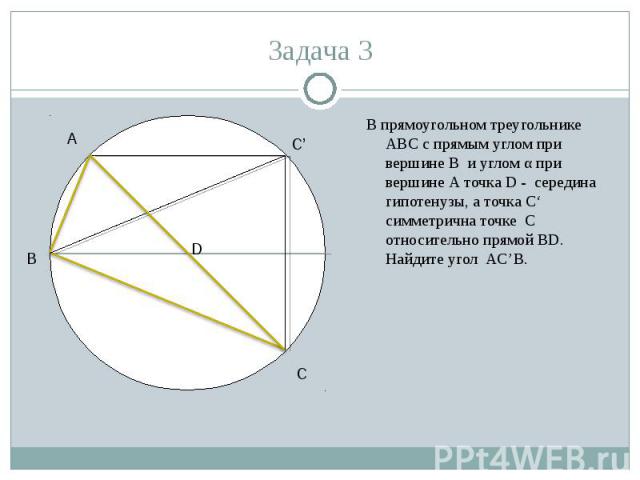
В прямоугольном треугольнике ABC с прямым углом при вершине B и углом α при вершине A точка D - середина гипотенузы, а точка C‘ симметрична точке C относительно прямой BD. Найдите угол AC’B. В прямоугольном треугольнике ABC с прямым углом при вершине B и углом α при вершине A точка D - середина гипотенузы, а точка C‘ симметрична точке C относительно прямой BD. Найдите угол AC’B.

Метод вспомогательной окружности при решении сложных нестандартных задач по геометрии очень быстро приводит к цели, позволяет решаемую задачу свести к элементарным задачам решения которых известны или легко могут быть получены. Вспомогательные построения позволяют сократить и упростить вычисления. Нестандартные дополнительные построения – один из самых эффективных приемов решения задач. Дополнительные (вспомогательные) построения – это существенный этап решения геометрических задач; стандартные приемы таких построений необходимо запоминать, а нестандартные – приобретать с опытом. Поэтому мы надеемся продолжить нашу работу в разделе стереометрия. Метод вспомогательной окружности при решении сложных нестандартных задач по геометрии очень быстро приводит к цели, позволяет решаемую задачу свести к элементарным задачам решения которых известны или легко могут быть получены. Вспомогательные построения позволяют сократить и упростить вычисления. Нестандартные дополнительные построения – один из самых эффективных приемов решения задач. Дополнительные (вспомогательные) построения – это существенный этап решения геометрических задач; стандартные приемы таких построений необходимо запоминать, а нестандартные – приобретать с опытом. Поэтому мы надеемся продолжить нашу работу в разделе стереометрия.

Спасибо за внимание! Спасибо за внимание!