Презентация на тему: «История теоремы Пифагора»

Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".

Кантор (крупнейший немецкий историк математики) считает, что равенство Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 и 4 м от одного конца. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Очень легко можно воспроизвести способ построения. Возьмём верёвку длиною в 12 м и привяжем к ней по цветной полоске на расстоянии 3 и 4 м от одного конца. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

Ван-дер-Варден (голландский математик) сделал следующий вывод: Ван-дер-Варден (голландский математик) сделал следующий вывод: "Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но её систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."

В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила верёвки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи верёвки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины). В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила верёвки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи верёвки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины).

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал её полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал её полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал".

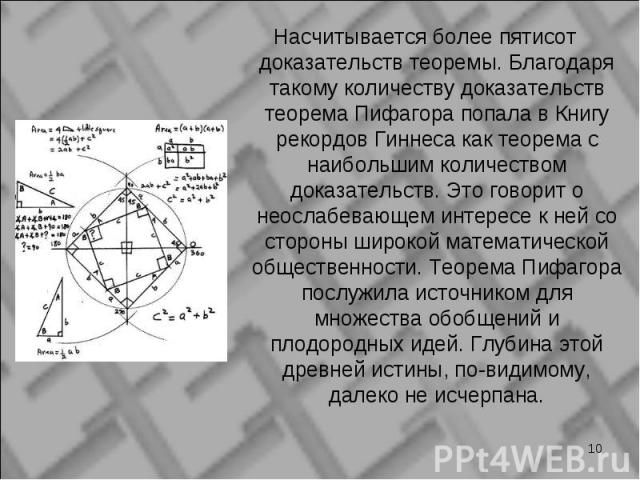
Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана. Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана.  

Приведём различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков. Приведём различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.

У Евклида эта теорема гласит (дословный перевод): У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Кремонским (начало 12 в.), в переводе на русский гласит: Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Кремонским (начало 12 в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".

В Geometria Culmonensis (около 1400 г.) теорема читается так: Also, wird das vierecke Feld, gemessen an der langen Wand, so also gross ist als bei beide Vierecke, bei zwei werden gemessen von den zwei Wanden des deren, bei zwei gemeinde, tretten in dem rechten Winkel. В Geometria Culmonensis (около 1400 г.) теорема читается так: Also, wird das vierecke Feld, gemessen an der langen Wand, so also gross ist als bei beide Vierecke, bei zwei werden gemessen von den zwei Wanden des deren, bei zwei gemeinde, tretten in dem rechten Winkel. В переводе это означает: "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".

В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

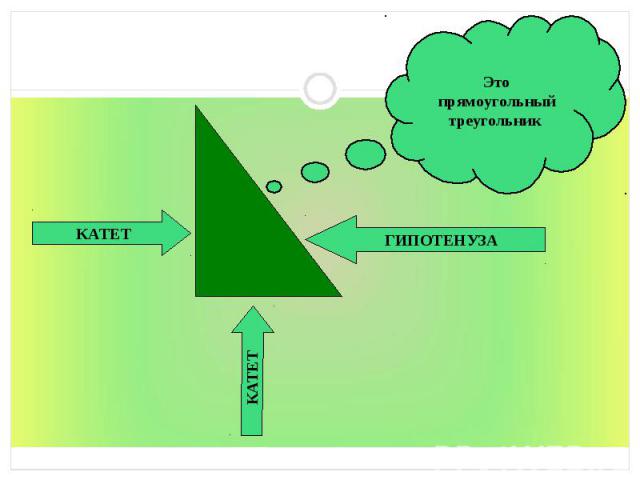
Существует три формулировки теоремы Пифагора: Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах. 3. Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.    

Теорема Пифагора – важнейшее утверждение геометрии. Даже те, кто в своей жизни навсегда «распрощался» с математикой, сохраняют воспоминания о «пифагоровых штанах». Причина такой популярности теоремы Пифагора объясняется её простотой, красотой, значимостью.

Если дан нам треугольник Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем: Катеты в квадрат возводим, Сумму степеней находим — И таким простым путем К результату мы придём.

Здесь вы можете увидеть доказательство теоремы Пифагора, которое основано на равновеликости фигур, из которых они состоят. Это доказательство считается одними из самых простых из-за своей наглядности. Здесь вы можете увидеть доказательство теоремы Пифагора, которое основано на равновеликости фигур, из которых они состоят. Это доказательство считается одними из самых простых из-за своей наглядности.

Почтовая марка по случаю переименования острова Самос в остров Пифагорейон. На марке надпись: « т.Пифагора. Эллас. 350 драхи». Почтовая марка по случаю переименования острова Самос в остров Пифагорейон. На марке надпись: « т.Пифагора. Эллас. 350 драхи».

Аддитивные доказательства - это доказательства, которые основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.  

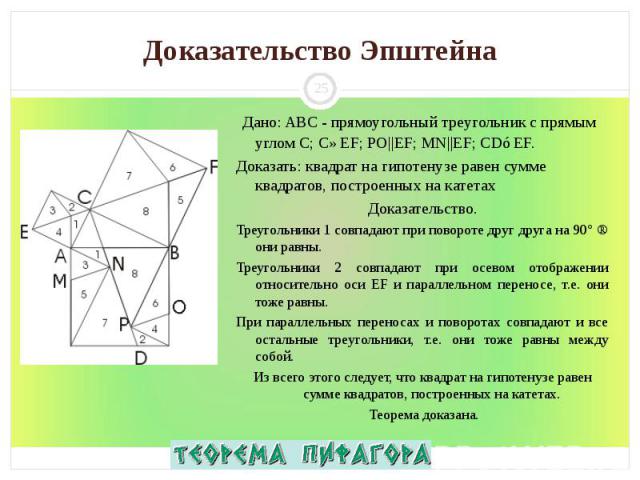
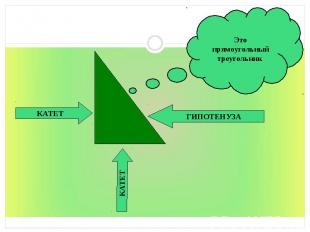
 Дано: ABC - прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF.  Дано: ABC - прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF. Доказать: квадрат на гипотенузе равен сумме квадратов, построенных на катетах Доказательство. Треугольники 1 совпадают при повороте друг друга на 90° ⇒ они равны. Треугольники 2 совпадают при осевом отображении относительно оси EF и параллельном переносе, т.е. они тоже равны. При параллельных переносах и поворотах совпадают и все остальные треугольники, т.е. они тоже равны между собой. Из всего этого следует, что квадрат на гипотенузе равен сумме квадратов, построенных на катетах. Теорема доказана.

Здесь вы найдете доказательства, для осуществления которых использовались дополнительные построения.

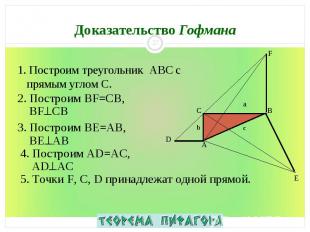
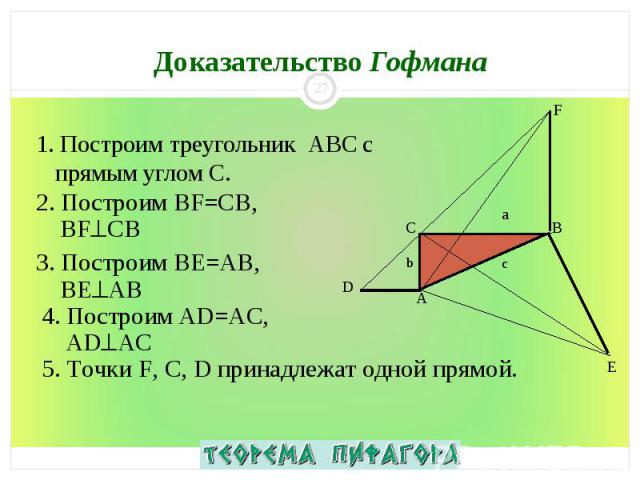
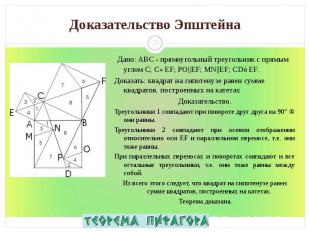
1. Построим треугольник ABC с прямым углом С. 1. Построим треугольник ABC с прямым углом С.

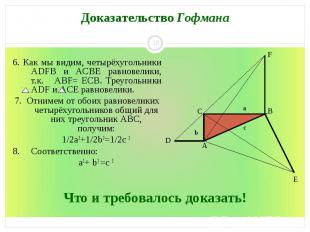
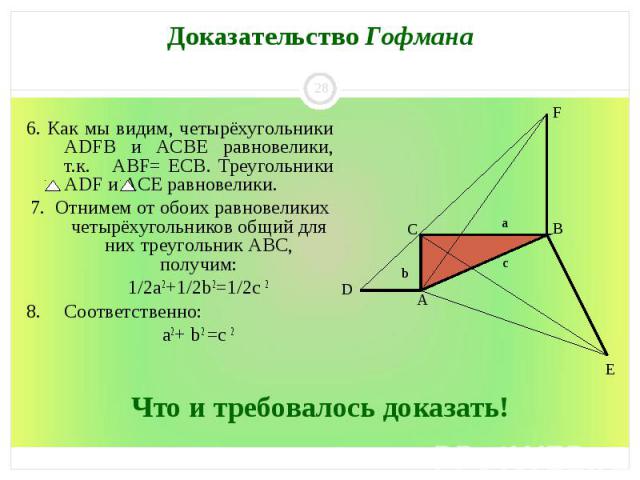
6. Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ABF= ЕCB. Треугольники ADF и ACE равновелики. 7. Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2 8. Соответственно: а2+ b 2 =с 2

Эти доказательства, основанные на применении в геометрии алгебраических формул. Это достаточно легкие доказательства, не требующие никаких дополнительных построений.

1. Площадь данного треугольника с одной стороны равна 0,5ab, 1. Площадь данного треугольника с одной стороны равна 0,5ab, с другой 0,5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r=0,5(a+b-c)).

Простейшие доказательства теоремы, для понимания которых достаточно одного взгляда на чертёж. Мы предлагаем несколько доказательств, которые не требуют пояснений. Это доказательства способом разложения квадратов на катетах и гипотенузе на отдельные фигуры. Простейшие доказательства теоремы, для понимания которых достаточно одного взгляда на чертёж. Мы предлагаем несколько доказательств, которые не требуют пояснений. Это доказательства способом разложения квадратов на катетах и гипотенузе на отдельные фигуры.

Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены рядом. Надо разделить эту фигуру всего на 3(!) части, чтобы сложить из них квадрат на гипотенузе. На иллюстрации наглядно дано это разрезание. Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах, расположены рядом. Надо разделить эту фигуру всего на 3(!) части, чтобы сложить из них квадрат на гипотенузе. На иллюстрации наглядно дано это разрезание.

Наряду с доказательствами методом сложения можно привести примеры доказательств при помощи вычитания, называемых также доказательствами методом дополнения. Общая идея таких доказательств заключается в следующем. Доказательства методом вычитания - доказательства при помощи вырезания определенных фигур из равных по площади частей. Наряду с доказательствами методом сложения можно привести примеры доказательств при помощи вычитания, называемых также доказательствами методом дополнения. Общая идея таких доказательств заключается в следующем. Доказательства методом вычитания - доказательства при помощи вырезания определенных фигур из равных по площади частей.

Прямая DG обязательно пройдет через C. Заметим теперь, что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.

Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С. По определению косинуса угла cosA=AD/AC=AC/AB. Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СD из вершины прямого угла С. По определению косинуса угла cosA=AD/AC=AC/AB. Отсюда АВ*AD=AC*АС.  Аналогично cos B=BD/BC=BC/AB. Отсюда АВ*BD=BC*BC. Складывая полученные результаты почленно и замечая, что AD+DB=AB, получим: AC*AC + BC*BC = AB*AB. Теорема доказана.

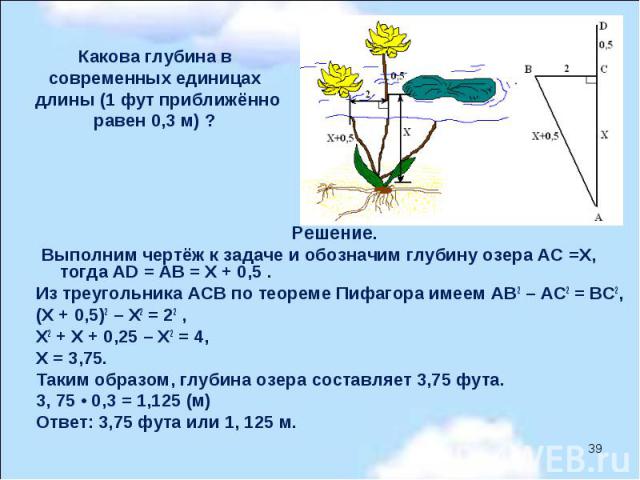
Над озером тихим Над озером тихим С полфута размером Высился лотоса цвет. Он рос одиноко, И ветер порывом Отнёс его в сторону. Нет Боле цветка над водой. Нашёл же рыбак его Ранней весною В двух футах от места, где рос. Итак, предложу я вопрос: “Как озера вода здесь глубока?”

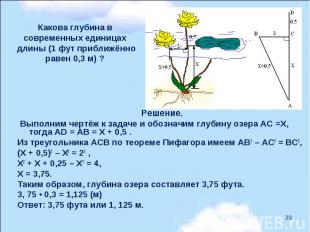
    Решение. Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 . Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2, (Х + 0,5)2 – Х2 = 22 , Х2 + Х + 0,25 – Х2 = 4, Х = 3,75. Таким образом, глубина озера составляет 3,75 фута. 3, 75 • 0,3 = 1,125 (м) Ответ: 3,75 фута или 1, 125 м.

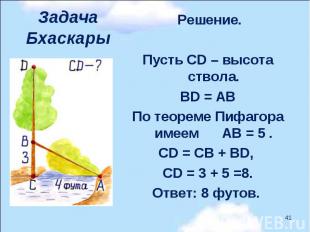
Решение. Решение.   Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ = 5 . CD = CB + BD, CD = 3 + 5 =8. Ответ: 8 футов.

На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба? На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

    Итак, в треугольнике АDВ: АВ2 =ВD2 +АD2 АВ2=302 +Х2 АВ2=900+Х2; в треугольнике АЕС: АС2= СЕ2+АЕ2 АС2=202+(50 – Х)2 АС2=400+2500 – 100Х+Х2 АС2=2900 – 100Х+Х2. Но АВ=АС, так как обе птицы пролетели эти расстояния за одинаковое время. Поэтому АВ2 =АС2 , 900+Х2 =2900 – 100Х+Х2, 100Х=2000, Х=20, АD=20. Значит, рыба была на расстоянии 20 локтей от большой пальмы. Ответ: 20 локтей.

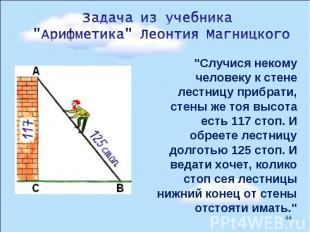
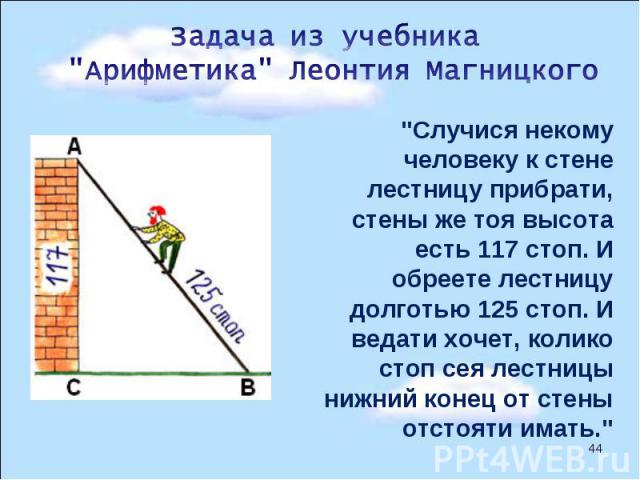
"Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать." "Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."  

 "Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.  "Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша? "

Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом: Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом: d2=2a², d= a.

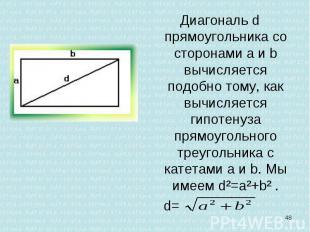
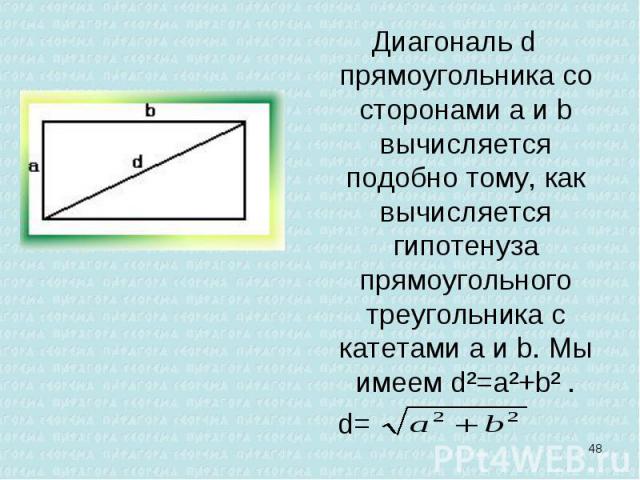
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b² . Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b² . d=

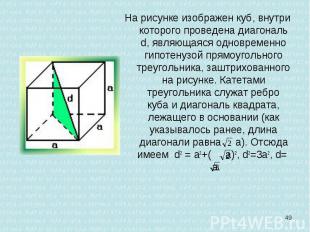
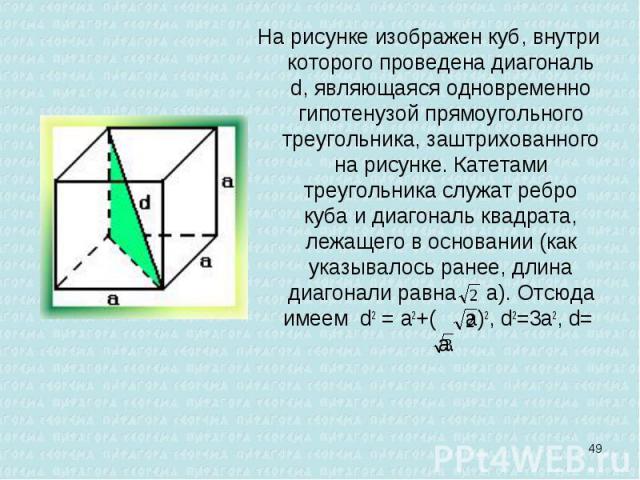
На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а). Отсюда имеем d2 = a2+( а)2, d2=3a2, d= a. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а). Отсюда имеем d2 = a2+( а)2, d2=3a2, d= a.

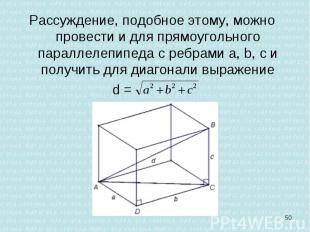
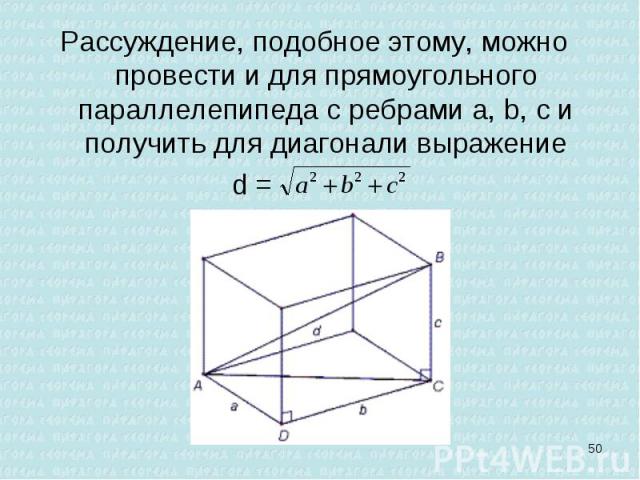
Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение d =

Считать приложения теоремы Пифагора только теоретическими - большая ошибка. Заметим, что расчёт площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь." Считать приложения теоремы Пифагора только теоретическими - большая ошибка. Заметим, что расчёт площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь."

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром p=b/6.

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли. В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все ещё ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.  

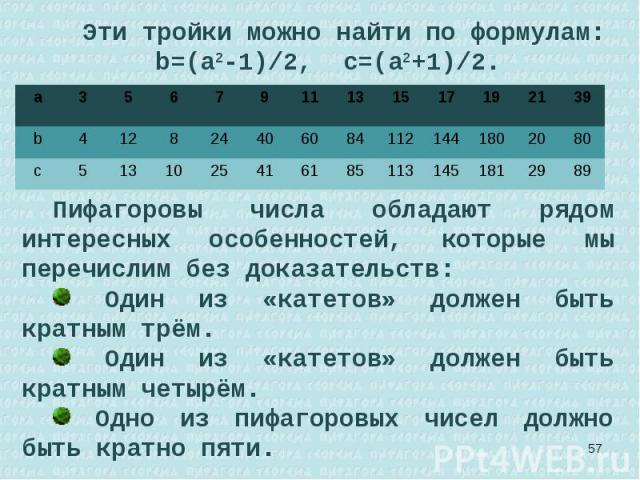
Изучение свойств натуральных чисел привело пифагорейцев к ещё одной «вечной» проблеме теоретической арифметики (теории чисел) — проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древнем Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение Изучение свойств натуральных чисел привело пифагорейцев к ещё одной «вечной» проблеме теоретической арифметики (теории чисел) — проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древнем Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение а2+b2=c2.

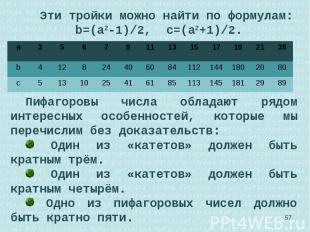
Сегодня эта задача именуется задачей Пифагора, а её решения — тройки натуральных чисел, удовлетворяющих уравнению (а2+b2=c2)— называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами а, b и целочисленной гипотенузой c. Сегодня эта задача именуется задачей Пифагора, а её решения — тройки натуральных чисел, удовлетворяющих уравнению (а2+b2=c2)— называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами а, b и целочисленной гипотенузой c.

Древневавилонский клинописный текст, содержащий 15 наборов пифагоровых троек, среди которых (четвёртая строка) есть тройка 12709, 13500, 18541: Древневавилонский клинописный текст, содержащий 15 наборов пифагоровых троек, среди которых (четвёртая строка) есть тройка 12709, 13500, 18541: 12709 + 13500 = 18541. Нью-Йорк. Плимптоновский фонд библиотеки Колумбийского университета.

И тем не менее вопрос об общем решении уравнения (а2+b2=c2) в натуральных числах был поставлен и решён только пифагорейцами. Общая постановка, какой бы то ни было математической задачи, была чужда как древним египтянам, так и древним вавилонянам. Только с Пифагора начинается становление математики как дедуктивной науки, и одним из первых шагов на этом пути было решение задачи о пифагоровых тройках. Первые решения уравнения (а2+b2=c2) античная традиция связывает с именами Пифагора и Платона. И тем не менее вопрос об общем решении уравнения (а2+b2=c2) в натуральных числах был поставлен и решён только пифагорейцами. Общая постановка, какой бы то ни было математической задачи, была чужда как древним египтянам, так и древним вавилонянам. Только с Пифагора начинается становление математики как дедуктивной науки, и одним из первых шагов на этом пути было решение задачи о пифагоровых тройках. Первые решения уравнения (а2+b2=c2) античная традиция связывает с именами Пифагора и Платона.

Многие при имени Пифагор вспоминают его теорему. Но неужели мы можем встречать эту теорему только в геометрии? Нет, конечно, нет! Теорема Пифагора встречается в разных областях наук. Например: в физике, астрономии, архитектуре и в других. Но так же Пифагор и его теорема воспеты в литературе. Многие при имени Пифагор вспоминают его теорему. Но неужели мы можем встречать эту теорему только в геометрии? Нет, конечно, нет! Теорема Пифагора встречается в разных областях наук. Например: в физике, астрономии, архитектуре и в других. Но так же Пифагор и его теорема воспеты в литературе. Существуют много легенд, мифов, рассказов, песен, притчей, небылиц об этой теореме и его авторе.

Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет. Много странных легенд дошло до наших дней о его рождении. Некоторые из них утверждают, что он не был обычным смертным человеком, а был одним из богов, принявших человеческий облик для того, чтобы войти в мир и учить человечество. Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет. Много странных легенд дошло до наших дней о его рождении. Некоторые из них утверждают, что он не был обычным смертным человеком, а был одним из богов, принявших человеческий облик для того, чтобы войти в мир и учить человечество.

За 1000 лет античной традиции реальные и вызывающие глубокое уважение к личности Пифагора сведения были перемешаны со множеством легенд, сказок и небылиц. Легенды наперебой объявляли Пифагора чудотворцем; сообщали, что у него было золотое бедро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким сверхчеловеческим голосом воскликнула: «Да здравствует Пифагор!», что в Тиррении он умертвил своим укусом ядовитую змею, унесшую жизни многих тирренцев, что он предсказывал землетрясения, останавливал повальные болезни, отвращал ураганы, укрощал морские волны. За 1000 лет античной традиции реальные и вызывающие глубокое уважение к личности Пифагора сведения были перемешаны со множеством легенд, сказок и небылиц. Легенды наперебой объявляли Пифагора чудотворцем; сообщали, что у него было золотое бедро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким сверхчеловеческим голосом воскликнула: «Да здравствует Пифагор!», что в Тиррении он умертвил своим укусом ядовитую змею, унесшую жизни многих тирренцев, что он предсказывал землетрясения, останавливал повальные болезни, отвращал ураганы, укрощал морские волны.

Порфирий рассказывает о Пифагоре такую историю: в «Таренте он увидел быка на разнотравье, жевавшего зеленые бобы, подошел к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух стал смеяться и сказал, что не умеет говорить по-бычьи; тогда Пифагор сам подошел к быку и прошептал ему что-то на ухо, после чего тот не только тут же пошел прочь от бобовника, но и более никогда не касался бобов, а жил с тех пор и умер в глубокой старости в Таренте при храме Геры, где слыл священным быком и кормился хлебом, который давали ему прохожие». Порфирий рассказывает о Пифагоре такую историю: в «Таренте он увидел быка на разнотравье, жевавшего зеленые бобы, подошел к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух стал смеяться и сказал, что не умеет говорить по-бычьи; тогда Пифагор сам подошел к быку и прошептал ему что-то на ухо, после чего тот не только тут же пошел прочь от бобовника, но и более никогда не касался бобов, а жил с тех пор и умер в глубокой старости в Таренте при храме Геры, где слыл священным быком и кормился хлебом, который давали ему прохожие».

Диоген Лаэртский, например, рассказывает так: «Появившись в Италии, Пифагор устроил себе жилье под землей, а матери велел записывать на дощечках всё, что происходит и когда, а дощечки спускать к нему, пока он не выйдет. Мать так и делала; а Пифагор, выждав время, вышел, иссохший, как скелет, предстал перед народным собранием и заявил, будто пришел из Аида, а при этом прочитал им обо всём, что с ними случилось. Все были потрясены прочитанным, плакали и рыдали, а Пифагора почли Богом. И тем не менее основной тон всех преданий о Пифагоре был один: Диоген Лаэртский, например, рассказывает так: «Появившись в Италии, Пифагор устроил себе жилье под землей, а матери велел записывать на дощечках всё, что происходит и когда, а дощечки спускать к нему, пока он не выйдет. Мать так и делала; а Пифагор, выждав время, вышел, иссохший, как скелет, предстал перед народным собранием и заявил, будто пришел из Аида, а при этом прочитал им обо всём, что с ними случилось. Все были потрясены прочитанным, плакали и рыдали, а Пифагора почли Богом. И тем не менее основной тон всех преданий о Пифагоре был один: «Ни о ком не говорят так много и так необычайно» (Порфирий).

Много ещё различных чудес можно было бы рассказать о Пифагоре. Но главное «чудо», прославившее в веках имя великого эллина, было в другом. Это чудо Пифагора состояло в том, что он вывел человечество из лабиринтов мифотворчества и богоискательства к берегам океана точного знания. Утренние купания пифагорейцев в волнах Ионического моря были и ежедневной прелюдией к плаванию по океану знания. Только целью плавания на сей раз были не поиски золотого руна, а поиски сокровища, куда более ценного. То были поиски истины. Много ещё различных чудес можно было бы рассказать о Пифагоре. Но главное «чудо», прославившее в веках имя великого эллина, было в другом. Это чудо Пифагора состояло в том, что он вывел человечество из лабиринтов мифотворчества и богоискательства к берегам океана точного знания. Утренние купания пифагорейцев в волнах Ионического моря были и ежедневной прелюдией к плаванию по океану знания. Только целью плавания на сей раз были не поиски золотого руна, а поиски сокровища, куда более ценного. То были поиски истины.  

Пифагор- это не только великий математик, но и великий мыслитель своего времени. Познакомимся с некоторыми его философскими высказываниями… Пифагор- это не только великий математик, но и великий мыслитель своего времени. Познакомимся с некоторыми его философскими высказываниями…

Мысль — превыше всего между людьми на земле. Мысль — превыше всего между людьми на земле. Не садись на хлебную меру (т. е. не живи праздно). По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих). Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык). Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду). В перстне изображений не носи (т. е. не выставляй напоказ перед людьми, как ты судишь и думаешь о богах).

Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение I книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придётся сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принёс в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя ещё Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики.

    Уделом истины не может быть забвенье, Как только мир её увидит взор, И теорема та, что дал нам Пифагор, Верна теперь, как в день её рожденья. За светлый луч с небес вознес благодаренье Мудрец богам не так, как было до тех пор. Ведь целых сто быков послал он под топор, Чтоб их сожгли как жертвоприношенье. Быки с тех пор, как только весть услышат, Что новой истины уже следы видны, Отчаянно мычат и ужаса полны: Им Пифагор навек внушил тревогу. Не в силах преградить той истине дорогу, Они, закрыв глаза, дрожат и еле дышат.

Так, оптимист Михайло Ломоносов (1711-1765) писал: «Пифагор за изобретение одного геометрического правила Зевесу принёс в жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось». Так, оптимист Михайло Ломоносов (1711-1765) писал: «Пифагор за изобретение одного геометрического правила Зевесу принёс в жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».

А вот ироничный Генрих Гейне (1797-1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не может доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам». А вот ироничный Генрих Гейне (1797-1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не может доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принёс в жертву бессмертным богам».

Когда был подожжён дом Милона, где собрались пифагорейцы, когда стали рушиться подпорки и перекрытия, державшие крышу, Пифагор в задумчивости сидел в центре большой залы. Великий мудрец и не помышлял сделать хоть одно движение к своему спасению. Тогда ученики Пифагора бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам, как по мосту, вышел из объятого пламенем дома. Пифагора спасли, но страшной ценой—ценой жизней его единомышленников. Оставшись один, Пифагор так затосковал, что удалился из города и там лишил себя жизни. Жизнь без продолжателей учения была для Пифагора лишена смысла. Когда был подожжён дом Милона, где собрались пифагорейцы, когда стали рушиться подпорки и перекрытия, державшие крышу, Пифагор в задумчивости сидел в центре большой залы. Великий мудрец и не помышлял сделать хоть одно движение к своему спасению. Тогда ученики Пифагора бросились в огонь и проложили в нем дорогу учителю, чтобы он по их телам, как по мосту, вышел из объятого пламенем дома. Пифагора спасли, но страшной ценой—ценой жизней его единомышленников. Оставшись один, Пифагор так затосковал, что удалился из города и там лишил себя жизни. Жизнь без продолжателей учения была для Пифагора лишена смысла.

Фрагмент фильма «Приключения Электроника» Ералаш

Учение Пифагора не погибло в кротонском пожаре. Подобранные горсткой оставшихся в живых учеников зерна этого учения не только были сохранены, но и дали обильные всходы. Благодарная память единомышленников сохранила для человечества имя Пифагора — выдающегося математического гения, творца акустики, основоположника теории музыки, «Коперника древней астрономии», основателя религиозного братства — прообраза средневековых монашеских орденов, богослова и реформатора, человека высокой нравственности, личности богатой, противоречивой и загадочной, стоящей на рубеже пробуждающейся науки и пышно цветущей мифологии. Учение Пифагора не погибло в кротонском пожаре. Подобранные горсткой оставшихся в живых учеников зерна этого учения не только были сохранены, но и дали обильные всходы. Благодарная память единомышленников сохранила для человечества имя Пифагора — выдающегося математического гения, творца акустики, основоположника теории музыки, «Коперника древней астрономии», основателя религиозного братства — прообраза средневековых монашеских орденов, богослова и реформатора, человека высокой нравственности, личности богатой, противоречивой и загадочной, стоящей на рубеже пробуждающейся науки и пышно цветущей мифологии.

И чем дальше неумолимое время уносит нас от времени Пифагора, тем острее видится поразительная прозорливость эллинского мудреца, объявившего два с половиной тысячелетия назад, что «Всё есть число». Если снять с этого тезиса мистическую паутину, то нам откроется гениальное пророчество, определившее весь последующий путь развития науки. Тогда древний пифагорейский тезис примет современное звучание: математика есть ключ к познанию всех тайн природы. И чем дальше неумолимое время уносит нас от времени Пифагора, тем острее видится поразительная прозорливость эллинского мудреца, объявившего два с половиной тысячелетия назад, что «Всё есть число». Если снять с этого тезиса мистическую паутину, то нам откроется гениальное пророчество, определившее весь последующий путь развития науки. Тогда древний пифагорейский тезис примет современное звучание: математика есть ключ к познанию всех тайн природы.

Именно так определяет роль Пифагора в истории естествознания современный американский математик и историк науки М. Клайн: «Но то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило всё последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы». Именно так определяет роль Пифагора в истории естествознания современный американский математик и историк науки М. Клайн: «Но то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило всё последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы».

В Абдерах в 430—420-х гг. до н. э. (т. е. менее чем через 100 лет после смерти Пифагора) произошло невиданное событие: в Абдерах были выпущены монеты с изображением Пифагора и подписью. Абдерские монеты — это не только первый в истории чеканный портрет философа, но это и первое на греческих монетах подписанное изображение человека. И таким человеком оказался не царь, не тиран, не полководец, а мудрец! Что касается Пифагора-математика, то он, видимо, навсегда останется первым и последним математиком в истории человечества, чей профиль удостоился столь высокой чести! В Абдерах в 430—420-х гг. до н. э. (т. е. менее чем через 100 лет после смерти Пифагора) произошло невиданное событие: в Абдерах были выпущены монеты с изображением Пифагора и подписью. Абдерские монеты — это не только первый в истории чеканный портрет философа, но это и первое на греческих монетах подписанное изображение человека. И таким человеком оказался не царь, не тиран, не полководец, а мудрец! Что касается Пифагора-математика, то он, видимо, навсегда останется первым и последним математиком в истории человечества, чей профиль удостоился столь высокой чести!

Самосская монета с изображением Пифагора. II-III вв. Прорисовка. Конечно, это не портрет Пифагора, а обобщённый образ учёного. Самосская монета с изображением Пифагора. II-III вв. Прорисовка. Конечно, это не портрет Пифагора, а обобщённый образ учёного.

Но для учёного важнее не внешние атрибуты славы, а признание и дальнейшая жизнь его идей. И здесь Пифагору также светила счастливая звезда. Идеями Пифагора пронизано творчество Платона — величайшего философа в истории человечества. Плотин, Порфирий, Ямвлих, Прокл, первая женщина философ и математик Гипатия, растерзанная толпой фанатиков-христиан,— все они были страстными приверженцами Пифагора. Неоплатонизм, уходящий корнями в древнее пифагорейство, стал мощным философским течением, идущим из античности в современность. Идеи неоплатоников питали Аврелия Августина (354—430) и Иоанна Скота Эриугену (810—877), Николая Кузанского (1401 —1464) и Джероламо Кардано (1501 —1576), Томмазо Кампанеллу (1568—1639) и Джордано Бруно (1548—1600), Фридриха Шеллинга (1775— 1854) и Георга Гегеля (1770—1831), Владимира Соловьева (1853—1900) и Сергея Булгакова (1871 —1944), Павла Флоренского (1882—1937?) и Алексея Лосева (1893—1988). Но для учёного важнее не внешние атрибуты славы, а признание и дальнейшая жизнь его идей. И здесь Пифагору также светила счастливая звезда. Идеями Пифагора пронизано творчество Платона — величайшего философа в истории человечества. Плотин, Порфирий, Ямвлих, Прокл, первая женщина философ и математик Гипатия, растерзанная толпой фанатиков-христиан,— все они были страстными приверженцами Пифагора. Неоплатонизм, уходящий корнями в древнее пифагорейство, стал мощным философским течением, идущим из античности в современность. Идеи неоплатоников питали Аврелия Августина (354—430) и Иоанна Скота Эриугену (810—877), Николая Кузанского (1401 —1464) и Джероламо Кардано (1501 —1576), Томмазо Кампанеллу (1568—1639) и Джордано Бруно (1548—1600), Фридриха Шеллинга (1775— 1854) и Георга Гегеля (1770—1831), Владимира Соловьева (1853—1900) и Сергея Булгакова (1871 —1944), Павла Флоренского (1882—1937?) и Алексея Лосева (1893—1988).

Заложенная Пифагором вера в красоту и гармонию природы, в мудрую простоту и целесообразность её законов, построенных на единых математических принципах, окрыляла творчество титанов современного естествознания от Иоганна Кеплера (1571 —1630) до Альберта Эйнштейна (1879—1955). Это и есть путеводная звезда современного естествознания, тот вечный кладезь мудрости, который открыл человечеству Пифагор. Заложенная Пифагором вера в красоту и гармонию природы, в мудрую простоту и целесообразность её законов, построенных на единых математических принципах, окрыляла творчество титанов современного естествознания от Иоганна Кеплера (1571 —1630) до Альберта Эйнштейна (1879—1955). Это и есть путеводная звезда современного естествознания, тот вечный кладезь мудрости, который открыл человечеству Пифагор.