Презентация на тему: Процесс Пуассона как универсальный вероятностный процесс для описания изменения параметров в системах взаимодействующих частиц

г. Луганск, ВНУ им. В. Даля, «Голубой корпус» А П П Ф 2008 Процесс Пуассона как универсальный вероятностный процесс для описания изменения параметров в системах взаимодействующих частиц Бранспиз Ю.А. Восточноукраинский национальный университет имени Владимира Даля

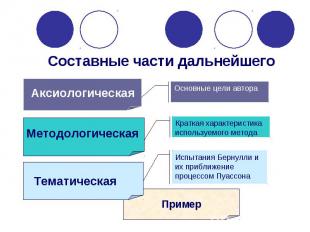
Аксиологическая Методологическая Тематическая Пример Основные цели автора Краткая характеристика используемого метода Испытания Бернулли и их приближение процессом Пуассона Составные части дальнейшего

1. «Законно» ли существование кафедр прикладной физики в университетах ? Аксиологическая часть Риторические вопросы ? Ответ на первый вопрос зависит от ответа на второй вопрос 2. Является ли «Прикладная физика» научной специальностью ?

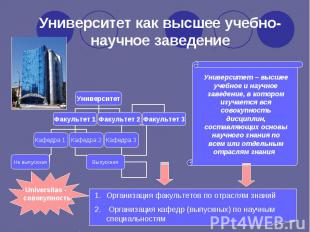
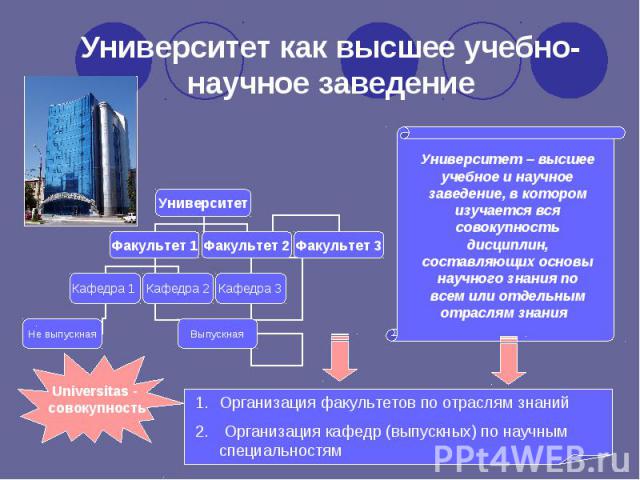
Университет Факультет 1 Факультет 2 Факультет 3 Кафедра 1 Кафедра 2 Кафедра 3 Выпускная Не выпускная Университет – высшее учебное и научное заведение, в котором изучается вся совокупность дисциплин, составляющих основы научного знания по всем или отдельным отраслям знания Организация факультетов по отраслям знаний Организация кафедр (выпускных) по научным специальностям Universitas - совокупность Университет как высшее учебно-научное заведение

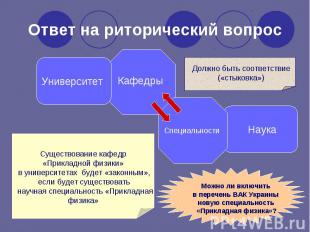
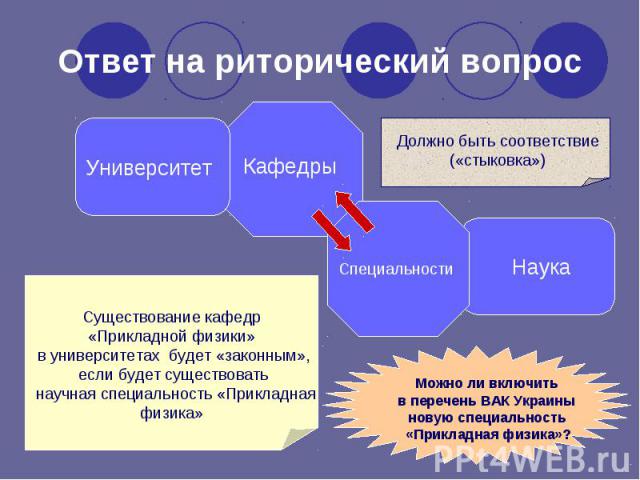
Наука Университет Кафедры Специальности Должно быть соответствие («стыковка») Существование кафедр «Прикладной физики» в университетах будет «законным», если будет существовать научная специальность «Прикладная физика» Можно ли включить в перечень ВАК Украины новую специальность «Прикладная физика»? Ответ на риторический вопрос

ТАКОЙ ВОТ ВОПРОС Пожалуй вопросом «что такое философия» можно заниматься лишь в позднюю пору, когда наступает старость, а с нею и время говорить конкретно. Действительно, библиография по нашей проблеме весьма скудна. Это такой вопрос, который задают , скрывая беспокойство, ближе к полуночи, когда больше спрашивать уже не о чем. Его ставили и раньше, все время, но слишком уж косвенно и или уклончиво, слишком искусственно, слишком абстрактно, излагая этот вопрос походя и свысока, не давая ему слишком глубоко себя зацепить. .. Слишком хотелось заниматься философией,.. не доходили до той грубости слога, когда наконец можно спросить – так что же это за штука, которой я занимался всю жизнь? Ж. Делез, Ф. Гваттари Аналогия 1 НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ?

Аналогия 2 История формирования технических наук 1. Описание природных процессов с целью управления ими для практического использования в инженерных приложениях. 2. Такое изменение реального объекта, которое полностью соответствует теории. 3. Перевод техническим путем реального объекта в идеальное состояние на основе использования открытых теорией законов природы – в целях практики. Реализация замысла: на основе теории – запустить реальный природный процесс в техническом устройстве , сделав его следствием человеческой деятельности. Г. Галилей Х. Гюйгенс НАУКА ЛИ ПРИКЛАДНАЯ ФИЗИКА ?

Аналогия 3 1. В процессе схематизации (формализации) решаемых задач. Общее и различие : 2. В процессе замещения реального процесса (явления) математической моделью. 3. В процессе формирования новых теоретических знаний . 4. В характере теоретических знаний и организации их использования Методология прикладной физики и методология физики

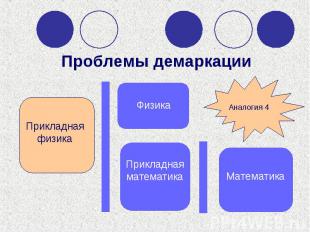
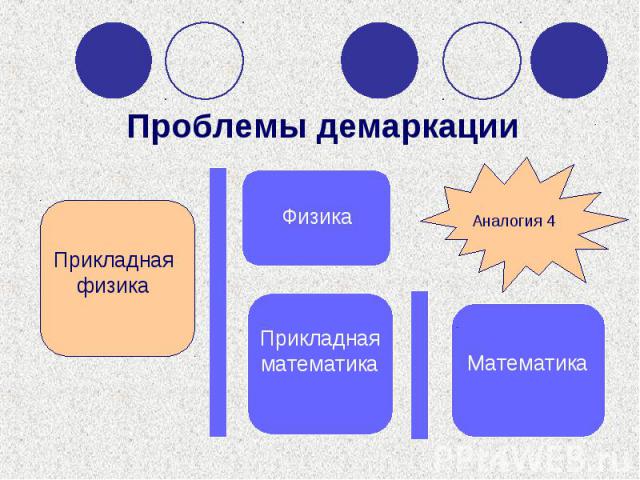
Прикладная физика Физика Прикладная математика Математика Аналогия 4 Проблемы демаркации

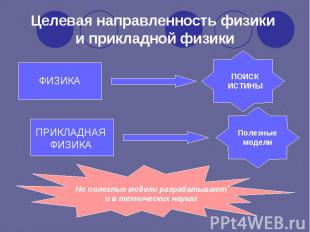
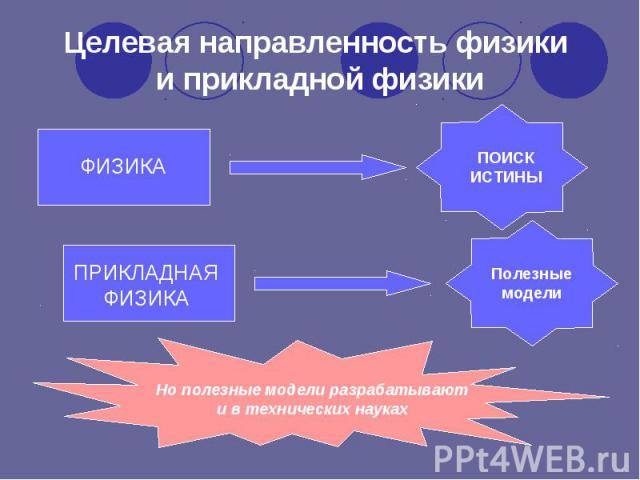
ФИЗИКА ПОИСК ИСТИНЫ ПРИКЛАДНАЯФИЗИКА Полезные модели Но полезные модели разрабатывают и в технических науках Целевая направленность физики и прикладной физики

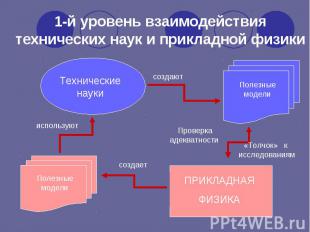
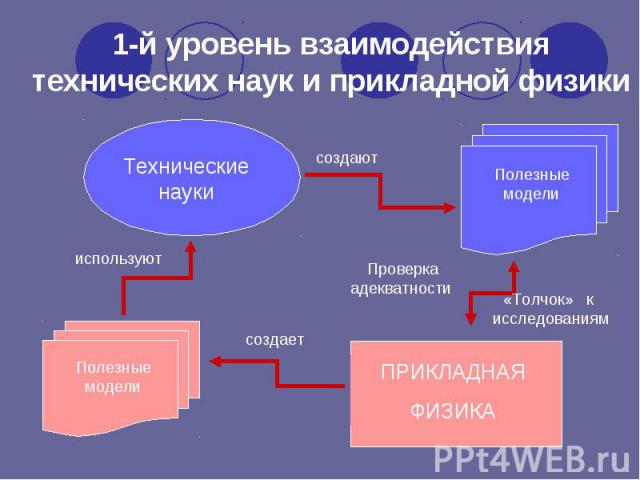
Полезные модели Технические науки создают используют Полезные модели ПРИКЛАДНАЯ ФИЗИКА создает Проверка адекватности «Толчок» к исследованиям 1-й уровень взаимодействия технических наук и прикладной физики

Применение формулировок, включающих неточно определенные понятия Применение утверждений, допускающих частные опровержения Уточнение в ходе исследования (открытость для уточнения) Использование аналогий и соответствия Использование доводов, основанных на частных данных экспериментов Моделирования дискретного континуумом и континуума дискретностью Применение практической бесконечности (знаки>> и

На дне глубокого сосуда Лежат спокойно n шаров. Поочередно их оттуда Таскают двое дураков. Сия работа им приятна, Они таскают t минут, И, вынув шар, его обратно Тотчас немедленно кладут. Ввиду занятия такого, Сколь вероятность велика, Что первый был глупей второго, когда шаров он вынул k? В.П. Скитович Схема испытаний Бернулли

Дано: 1. Некоторое испытание (физический процесс). 2. В результате испытания событие S может произойти или не произойти 3. Вероятность события S в каждом из испытаний не зависит от результата остальных испытаний и равна p. 4. Осуществление события S – «успех», не осуществление – «неудача». Пример: 1. S – изменение некоторого параметра в системе многих частиц в сторону увеличения («успех) или уменьшения («неудача»); каждое такое изменение – испытание Бернулли. 2. Увеличение некоторого параметра в системе многих частиц на величину менее («успех») или более («неудача») данной. Определение испытаний Бернулли

1. Вероятность того, что в n испытаниях Бернулли событие S произойдет k раз определяется равенством где - число сочетаний из n по k. , 2. Пусть n стремится к бесконечности и p→0. Пусть также имеет место предел np→λ>0. Тогда для любого k>0 вероятность получить k «успехов» в n испытаниях схемы Бернулли с вероятностью успеха p стремится к величине То есть, имеет место предельный переход Закономерности испытаний Бернулли

Испытания Бернулли как процесс Пуассона Определение процесса Пуассона: Вероятность того, что в интервале времени ( ) произойдет изменение состояния равна . Тогда вероятность того, что в момент времени система находится в состоянии равна . Эту вероятность можно интерпретировать и как вероятность того, что за время t произойдет х изменений. Если , то получаем процесс рождения и гибели Для любого физического процесса всегда можно подобрать соответствующий вид зависимости !

Уравнение Чепмена-Колмогорова для изменения значения параметра х Это уравнение - уравнение полной вероятности - вероятность увеличения значения параметра Х - вероятность уменьшения значения параметра Х - значение параметра X в момент времени t (Ч-К)

Общее уравнение для плотности вероятности изменения значения параметра х Применяя к слагаемым уравнения (Ч-К) разложения в ряд Тейлора получим (ОУПВ) И справа и слева в (ОУПВ) – бесконечное число слагаемых

Условие для интервала времени наблюдения за изменением параметра х Предельный переход применим не для всех процессов 1 Нет бесконечного числа слагаемых слева ( * ) Конкретизация вида уравнения для плотности вероятности изменения значения параметра

2 Ограничение числа слагаемых в правой части уравнения (*) связано с установлением взаимосвязи между характеристиками изменения параметра х: и Порядок малости определяет порядок малости Порядок малости не может превышать порядок малости величины , Конкретизация вида уравнения для плотности вероятности изменения значения параметра

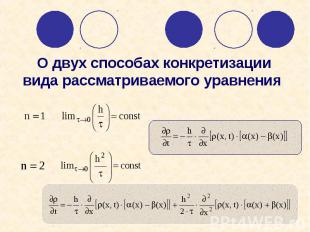
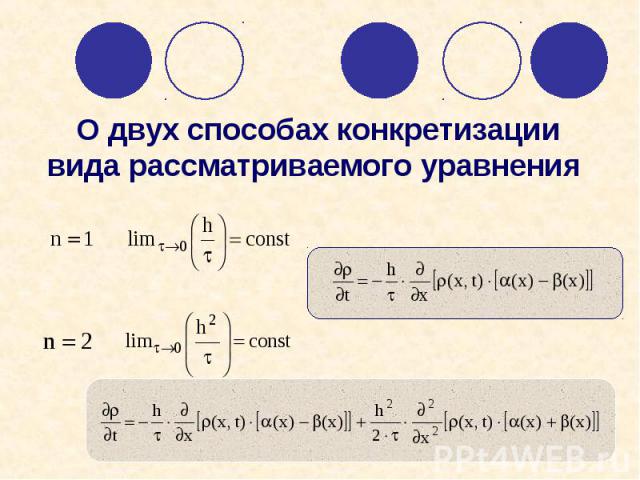
О двух способах конкретизации вида рассматриваемого уравнения

= =const = Уравнение диффузии мс дрейфом (Эйнштейна-Смолуховского) Реализация одного из способов

1-й способ описания (процесс Пуассона) 2-й способ описания (диффузия с дрейфом) Соответствующим подбором соотношений констант, характеризующих два способа описания случайного изменения параметра х , можно добиться, что средние и дисперсии этих способов будут одинаковы К сравнению способов конкретизации вида уравнения для плотности вероятности случайного изменения значения параметра х

Доклад закончен. Благодарю за внимание