Презентация на тему: Гармонические колебания точки

08.12. 2010 Учитель математики – Рабочая Т.А. Учитель физики – Самуйлова Е.Н. 10 класс 5klass.net

Цели урока: Систематизировать знания о свойствах тригонометрических функций. Продолжить формирование умений преобразования графиков тригонометрических функций. Рассмотреть физический смысл величин, входящих в уравнение гармонических колебаний. Установить межпредметные связи математика-физика по данной теме.

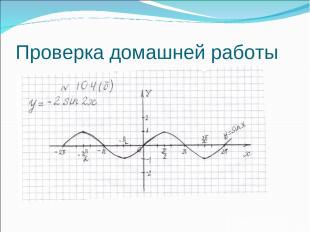
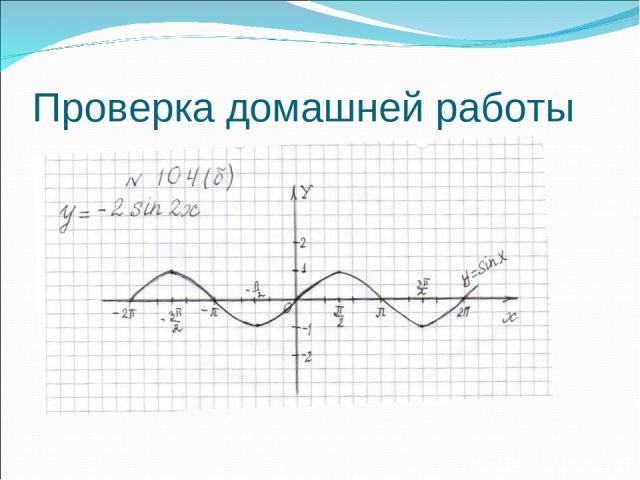
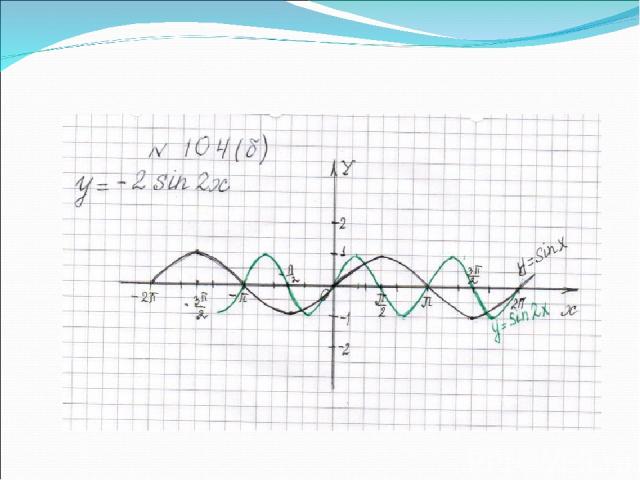
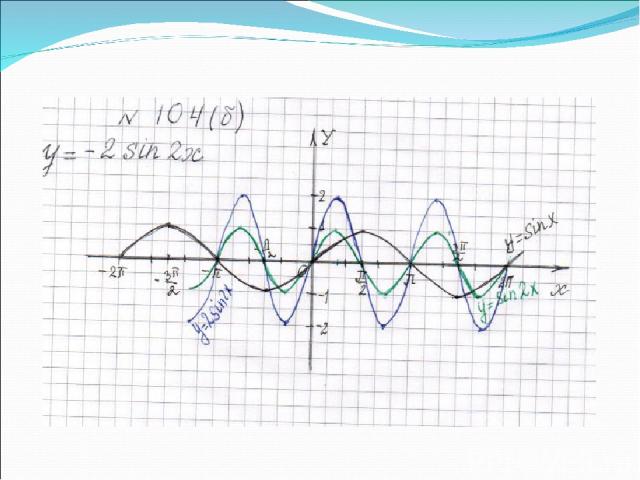
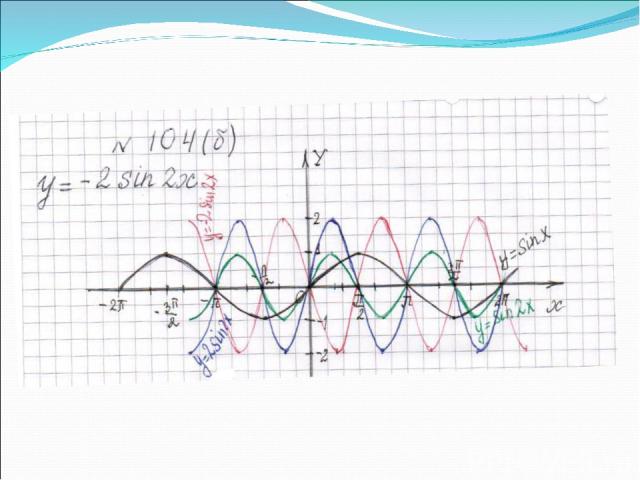
Проверка домашней работы

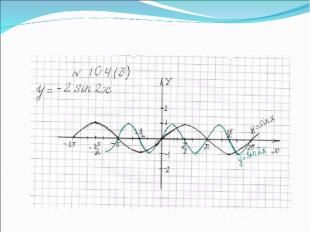
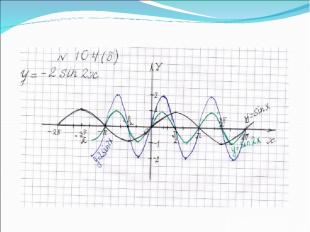
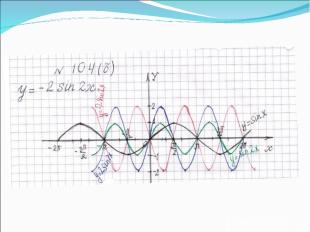
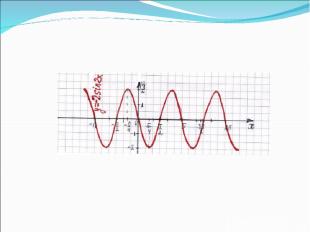
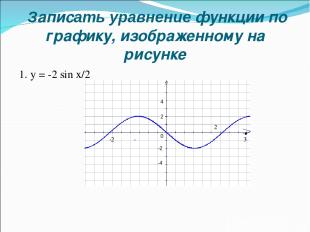
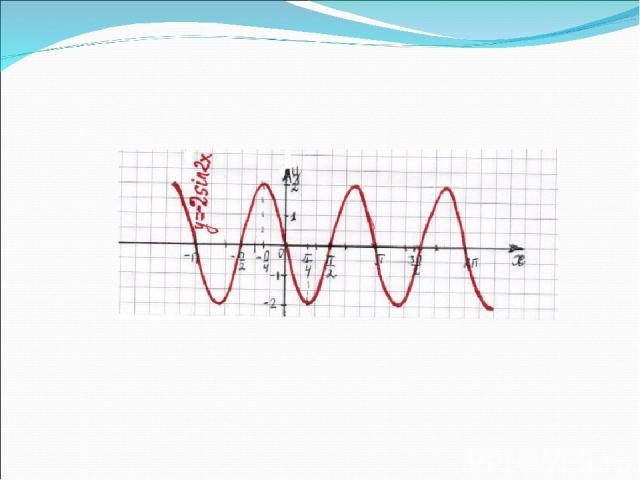
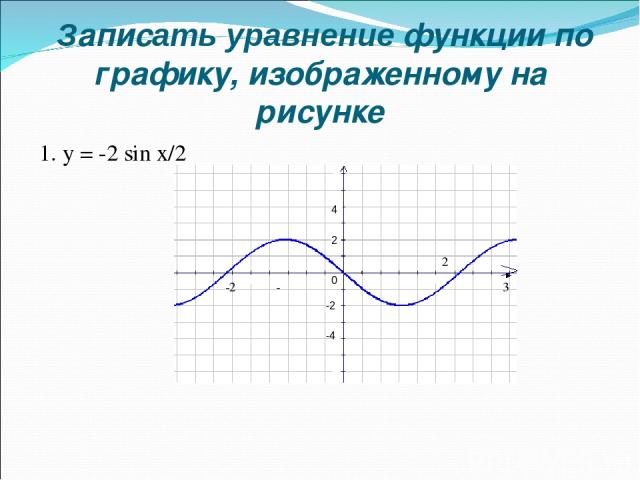
Записать уравнение функции по графику, изображенному на рисунке 1. y = -2 sin x/2 2 4 -2 -4 π 2π 3π - π -2π 0

Найти область значений и период функции, если: б) y = 0,3 sin x/3; а) y = ½ cos 2x; в) y = -5 cos (3x - π/3); г) y = 3 sin (2x + 2π/3).

( 1792 – 1856 ) Нет ни одной области математики, которая когда - нибудь не окажется применимой к явлениям действительного мира. Н.И. Лобачевский

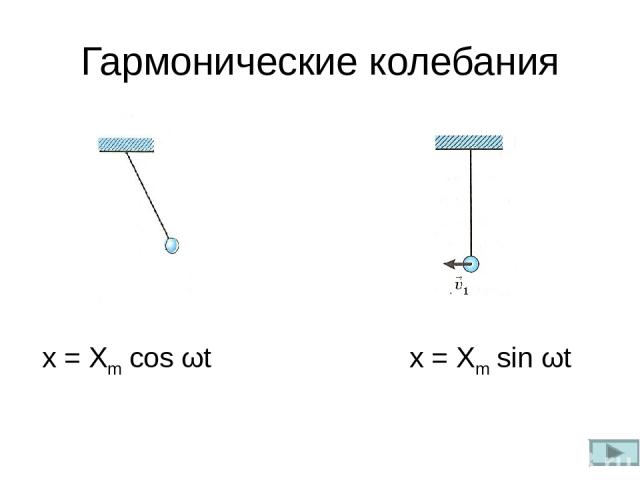
Гармонические колебания y = A sin (ωt + φ0) или y = A cos (ωt + φ0) уравнение гармонических колебаний

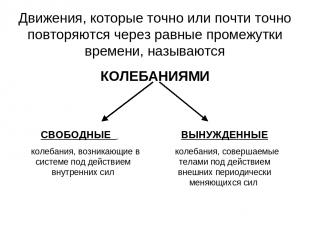
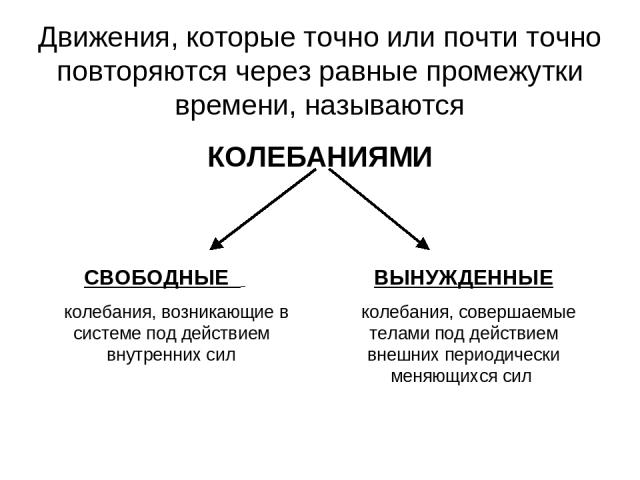
Движения, которые точно или почти точно повторяются через равные промежутки времени, называются КОЛЕБАНИЯМИ СВОБОДНЫЕ колебания, возникающие в системе под действием внутренних сил ВЫНУЖДЕННЫЕ колебания, совершаемые телами под действием внешних периодически меняющихся сил

УСЛОВИЯ ВОЗНИКНОВЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ при выведении тела из положения равновесия в системе должна возникнуть сила, стремящаяся вернуть его в положение равновесия; силы трения в системе должны быть достаточно малы.

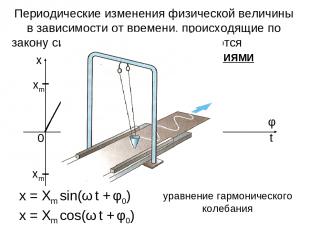
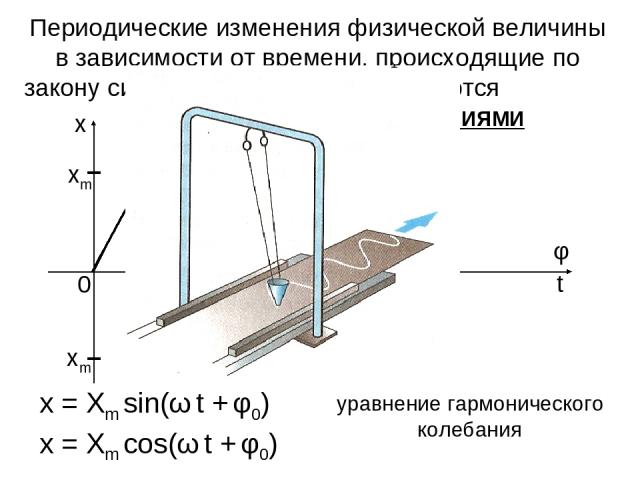
Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются ГАРМОНИЧЕСКИМИ КОЛЕБАНИЯМИ x = Xm sin(ω t + φ0) уравнение гармонического колебания x = Xm cos(ω t + φ0)

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ Xm – модуль максимального смещения точки от положения равновесия называется амплитудой; x – смещение точки от положения равновесия в данный момент времени (мгновенное значение). x = Xm sin(ω t + φ0) φ = ωt + φ0 – фаза колебаний, которая определяет состояние колебательной системы в любой момент времени; φ = [ рад ]

число колебаний в единицу времени называется частотой; υ = 1/Т – линейная частота колебаний υ= n/t; υ= [ Гц ] ω = 2π/Т –циклическая частота колебаний ω = [ рад/с ] Т – время одного полного колебания называется периодом; Т = t/n, где n – число полных колебаний ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ x = Xm sin(ω t + φ0)

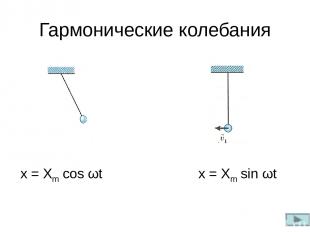
Гармонические колебания x = Xm cos ωt x = Xm sin ωt

U(t) = 0,25 sin 50πt; U(t) = Um sin ωt; Um = 0,25 В; ω = 50π; ω = 2πυ; 50π = 2πυ; υ = 50π/2π υ = 25 Гц; T = 1/υ , T = 1/ 25 Гц, T = 0,04c. Определение основных характеристик колебательного движения по закону

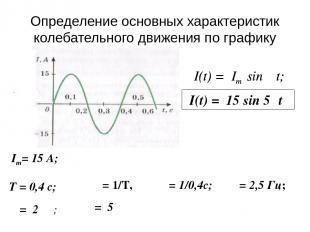
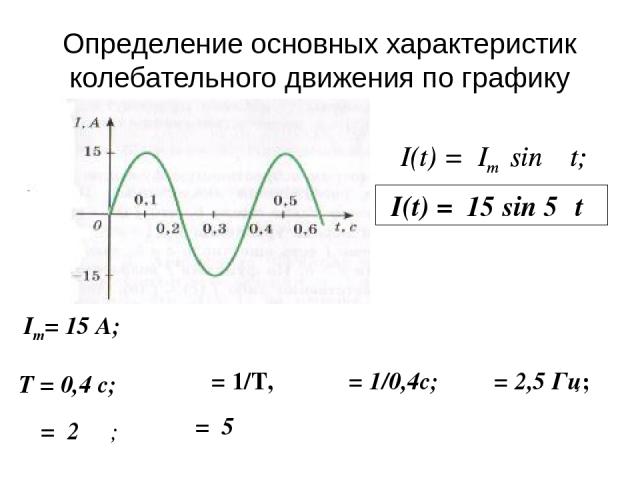
Определение основных характеристик колебательного движения по графику Im= 15 А; υ = 1/Т, υ = 1/0,4с; υ = 2,5 Гц; I(t) = Im sin ωt; ω = 2πυ; ω = 5π I(t) = 15 sin 5πt Т = 0,4 с; I(t) = Im sin ωt;

Звуковые волны Звук – это колебания, распространяющиеся в упругой среде. Вибрирующий источник передаёт колебания молекулам воздуха и давление его то увеличивается, то уменьшается. Изменение давления распространяется от источника во все стороны – возникает звуковая волна.

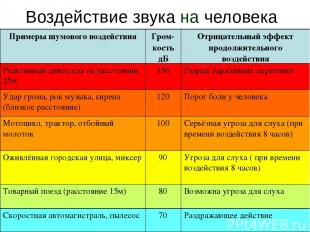
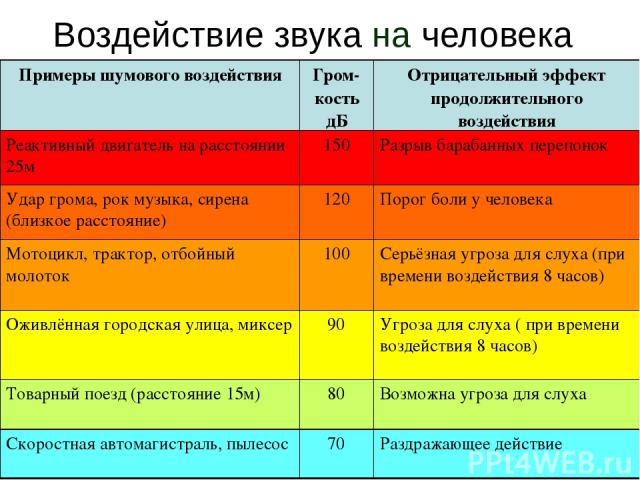
Воздействие звука на человека Примеры шумового воздействия Гром-кость дБ Отрицательный эффект продолжительного воздействия Реактивный двигатель на расстоянии 25м 150 Разрыв барабанных перепонок Удар грома, рок музыка, сирена (близкое расстояние) 120 Порог боли у человека Мотоцикл, трактор, отбойный молоток 100 Серьёзная угроза для слуха (при времени воздействия 8 часов) Оживлённая городская улица, миксер 90 Угроза для слуха ( при времени воздействия 8 часов) Товарный поезд (расстояние 15м) 80 Возможна угроза для слуха Скоростная автомагистраль, пылесос 70 Раздражающее действие

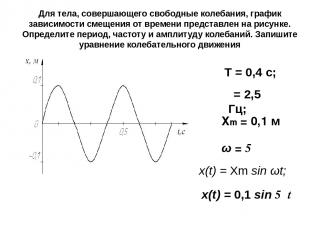
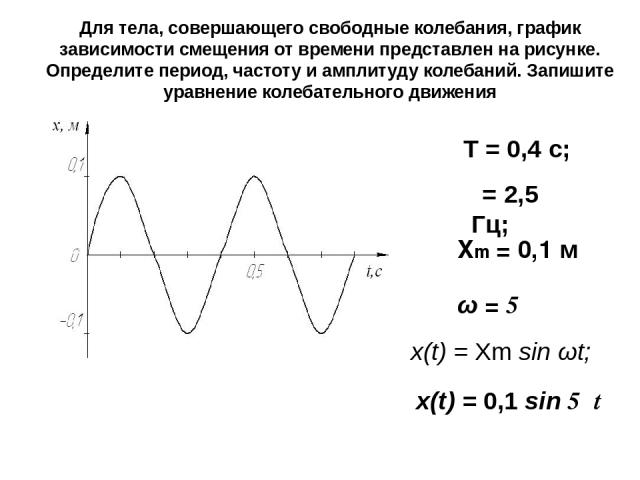
Для тела, совершающего свободные колебания, график зависимости смещения от времени представлен на рисунке. Определите период, частоту и амплитуду колебаний. Запишите уравнение колебательного движения Т = 0,4 с; υ = 2,5 Гц; Xm = 0,1 м ω = 5π x(t) = Xm sin ωt; x(t) = 0,1 sin 5πt

Самостоятельная работа Координата движущегося тела изменяется по указанному закону. Найдите амплитуду, период и частоту колебания. Вычислите координату тела в момент времени t1, если: 1 вариант 2 вариант х(t) = 5 cos (3πt + π/3) х(t) = 0,5 cos (πt/2 + π/3) t1 = 4с t1 = 8с

1 вариант 2 вариант Xm= 5 м T = 2/3 c υ = 1,5 Гц x(t1) = 2,5 м Xm= 0,5 м T = 4 c υ = 1/4 Гц x(t1) = 0,25 м Проверка самостоятельной работы

Домашнее задание: 1. Постройте график функции: а) у = -2 соs 2(x + π/4) ; б) y = 0,5 sin(0,5x – π/6). 2. Маятник вывели из положения равновесия и отпустили, после чего он совершил 50 колебаний за 1 мин 40 c с амплитудой 10 см. Напишите уравнение зависимости х(t).