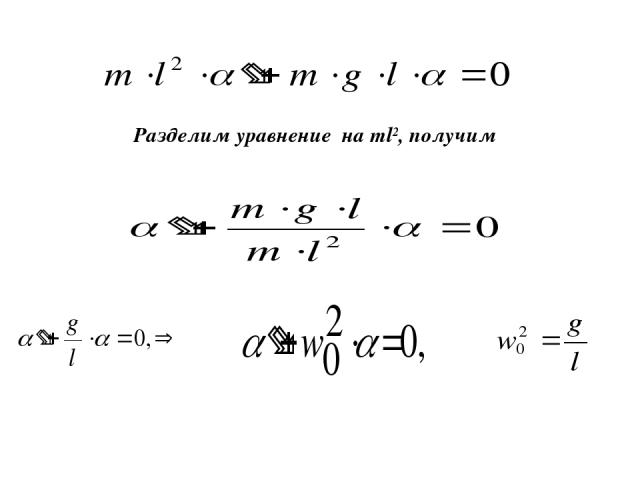Презентация на тему: Гармонические колебания и маятники

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ 900igr.net

План лекции. 1. Колебательное движение. Гармоническое колебание 2. Скорость и ускорение гармонического колебания 3. Энергия гармонического колебательного движения 4. Свободные колебания. Гармонический осциллятор 5. Пружинный, математический и физический маятники 6. Вынужденные колебания. Резонанс. Автоколебания 7. Примеры проявления резонансных явлений в живых организмах 8. Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение взаимно перпендикулярных колебаний

Колебательное движение. Гармоническое колебание

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения. Колебания широко распространены в природе и технике. Колебательные процессы лежат в основе таких отраслей техники как электротехника, радиотехника и т.д.

Колебаниями - называются процессы, отличающиеся той или иной степенью повторяемости (качели, ветка дерева, фазы луны, морские приливы и отливы, пульсовая волна, сердце, гортань…). В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными.

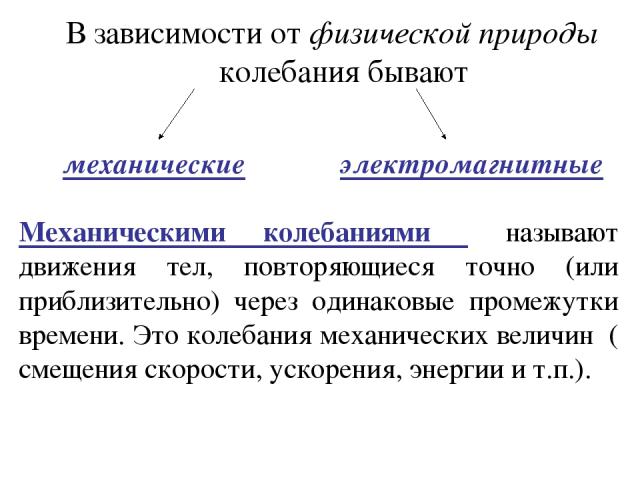
В зависимости от физической природы колебания бывают механические электромагнитные Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Это колебания механических величин ( смещения скорости, ускорения, энергии и т.п.).
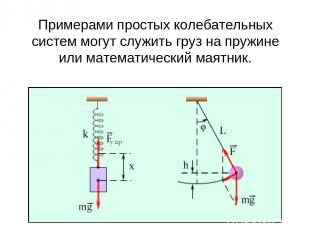
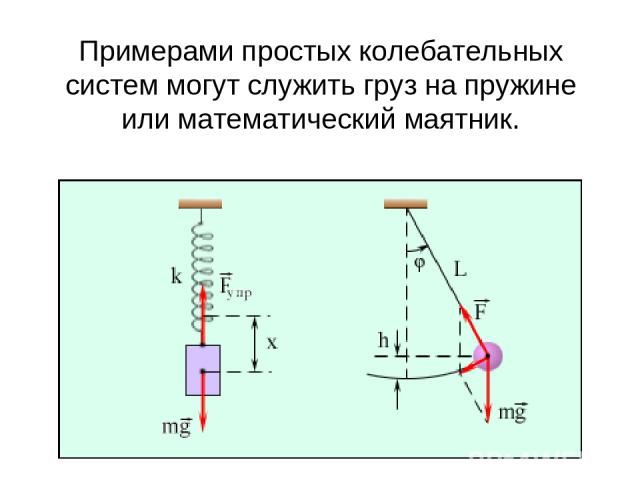
Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

В зависимости от характера воздействия на колеблющуюся систему, различают: Свободные колебания, возникающие при однократном воздействии внешней силы (первоначальном сообщении энергии) и при последующем отсутствии внешних воздействий на колебательную систему(колебания груза на пружине или колебания маятника являются свободными колебаниями). 2. Вынужденные – возникающие под действием внешних, периодически изменяющихся сил(при периодическом поступлении энергии извне к колебательной системе) (колебание моста при прохождении солдат, идущих в ногу).

3. Автоколебания – возникающие под действием внутренних периодических сил(при периодическом поступлении энергии от собственного источника внутри колебательной системы) (маятник часов получает толчки в момент прохождения её через среднее положение). 4. Параметрические колебания - происходит периодическое изменение, какого- либо параметра системы за счет внешнего воздействия (например, длины нити математического маятника). Колебательная система - это система тел, совершающая колебания.
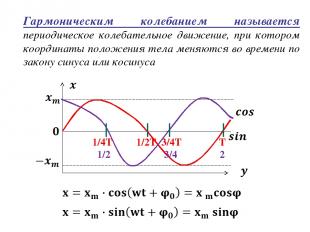
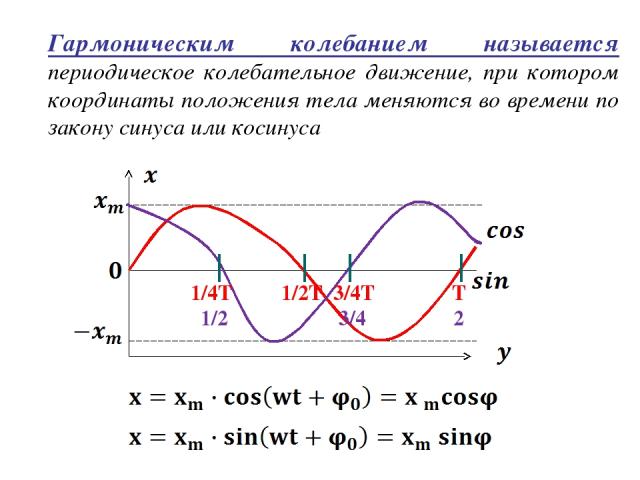
Гармоническим колебанием называется периодическое колебательное движение, при котором координаты положения тела меняются во времени по закону синуса или косинуса 1/4T 1/2T 3/4T T 1/2π π 3/4π 2π

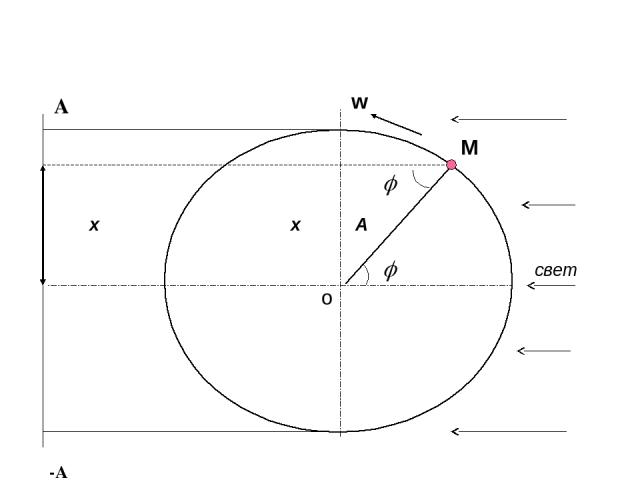
Выведем уравнение гармонического колебания при помощи установки, состоящей из экрана и вращающегося диска с закреплённым на нём непрозрачным шариком
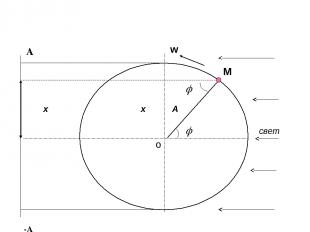
M x x А свет -А о А w

Пусть материальная точка М движется против часовой стрелки по окружности радиусом А. Тогда её проекция на экране совершает периодические колебания около положения равновесия в пределах от А до –А. Выразим величину смещения x в любой момент времени. уравнение гармонического колебания (1)
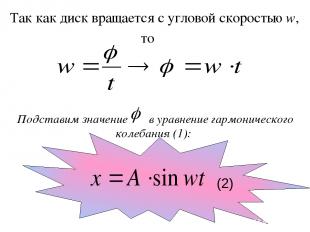
Так как диск вращается с угловой скоростью w, то Подставим значение в уравнение гармонического колебания (1): (2)

Если диск совершает полный оборот
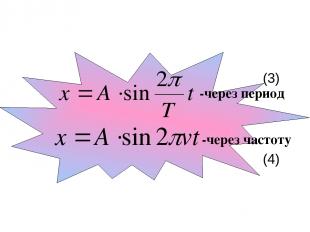
(3) -через период -через частоту (4)

Основные характеристики гармонического колебания: x- смещение отклонение от положения равновесия в данный момент времени (может быть >0 и
![w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза к w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза к](https://fs3.ppt4web.ru/images/132073/189483/310/img17.jpg)
w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени. 6. v- частота- число колебаний в единицу времени.

Если к началу наблюдения фаза имела некоторое начальное значение , то уравнение запишется: гармоническое колебание с начальной фазой (5) 7. φ- угловая физическая величина, показывающая положение и направление движения колебательной системы в данный момент времени,[рад] 8. φ0- начальная фаза,[рад]

Скорость и ускорение гармонического колебания.

Скорость - гармонических колебаний есть первая производная смещения по времени. Известно, что скорость для гармонического колебания определяется следующим образом скорость гармонического колебания (6)

ускорение при гармоническом колебании (7)

Колебательное движение выполняется под действием силы, которая может быть определена по второму закону Ньютона: , но ускорение при гармонических колебаниях определяется по формуле , подставим значение ускорения во второй закон Ньютона, то , но , то (8) сила действующая на колеблющееся тело

Она пропорциональна смещению, знак «-» указывает на, то что сила направлена в противоположную сторону относительно смещения квазиупругая сила, вызывающая колебательные движения (9)

Энергия гармонического колебательного движения

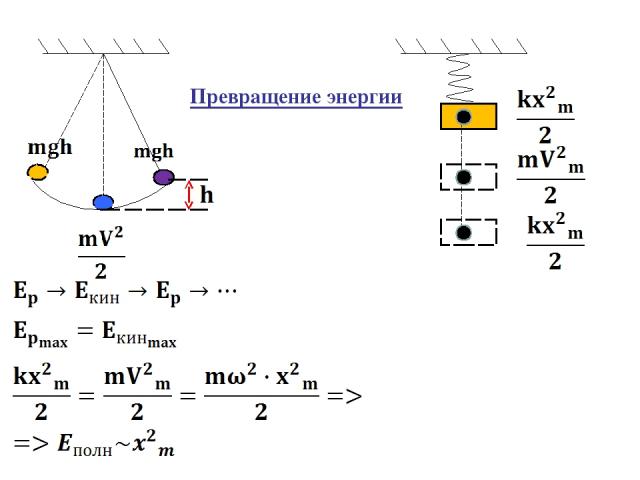
Квазиупругая сила является консервативной и поэтому полная механическая энергия системы остаётся постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно, причём в моменты наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего максимального значения. (10) (11)
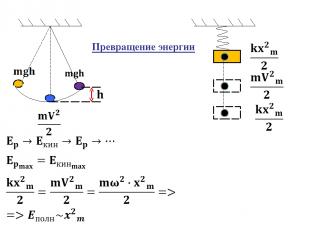
Превращение энергии

Свободные колебания. Гармонический осциллятор.

Система, движущая под действием упругой среды называется - одномерным гармоническим осциллятором. Известно, что ускорение при гармоническом колебании определяется следующим образом: или , но то,

(12) уравнение движение гармонического осциллятора

Пружинный, математический и физический маятники.

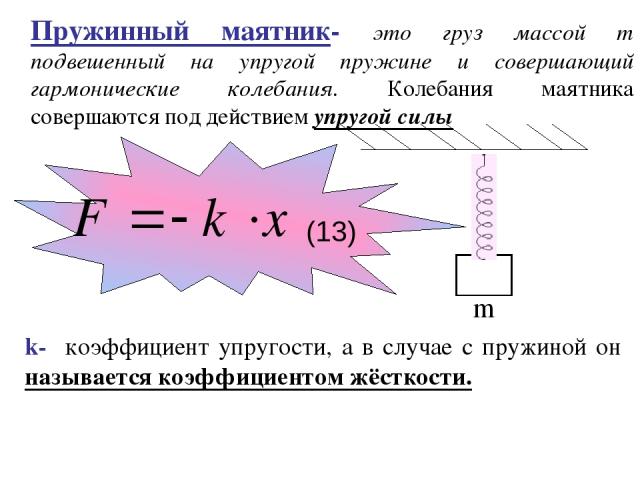
Пружинный маятник- это груз массой m подвешенный на упругой пружине и совершающий гармонические колебания. Колебания маятника совершаются под действием упругой силы m k- коэффициент упругости, а в случае с пружиной он называется коэффициентом жёсткости. (13)
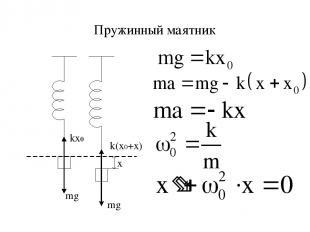
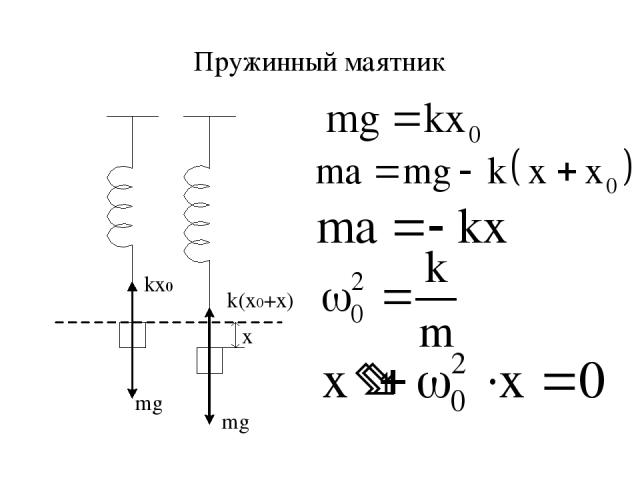
Пружинный маятник

Уравнение движения маятника записывается: Ускорение- это вторая производная смещения по времени: т.к Разделим обе части уравнения на m, то получим (14)

Сравним между собой уравнения (12) и (14), очевидно, , а период колебания подставим в формулу периода колебания значение w, что то (15) период колебания пружинного маятника.
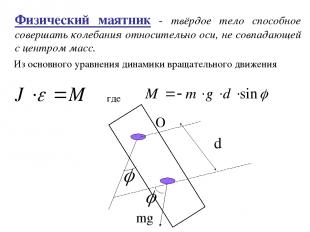
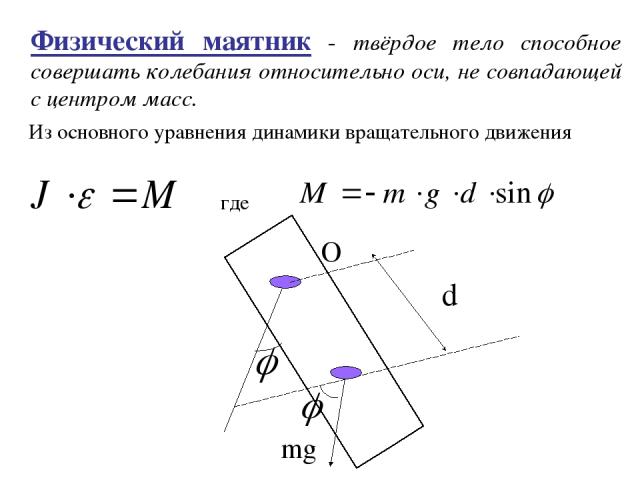
Физический маятник - твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс. d O mg Из основного уравнения динамики вращательного движения где
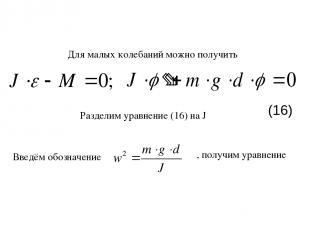
Разделим уравнение (16) на J Введём обозначение , получим уравнение Для малых колебаний можно получить (16)

Период колебания физического маятника ,которое аналогично полученному ранее (17)
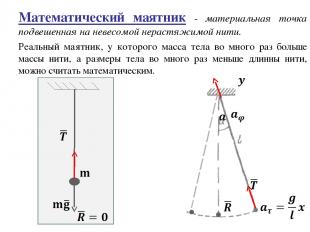
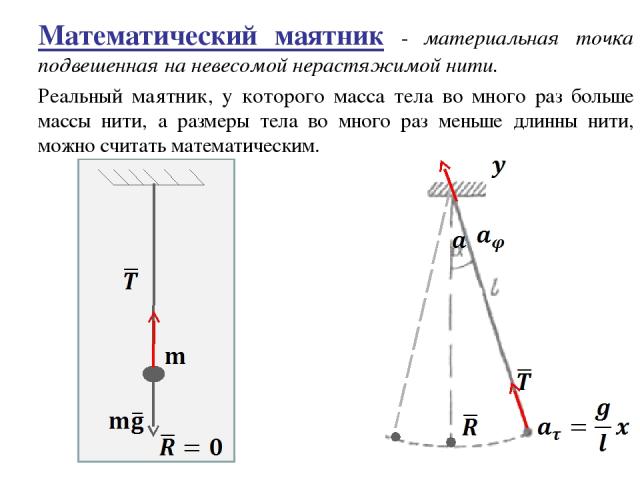
Математический маятник - материальная точка подвешенная на невесомой нерастяжимой нити. Реальный маятник, у которого масса тела во много раз больше массы нити, а размеры тела во много раз меньше длинны нити, можно считать математическим.
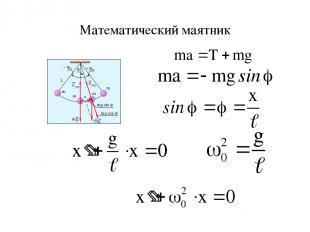
Математический маятник

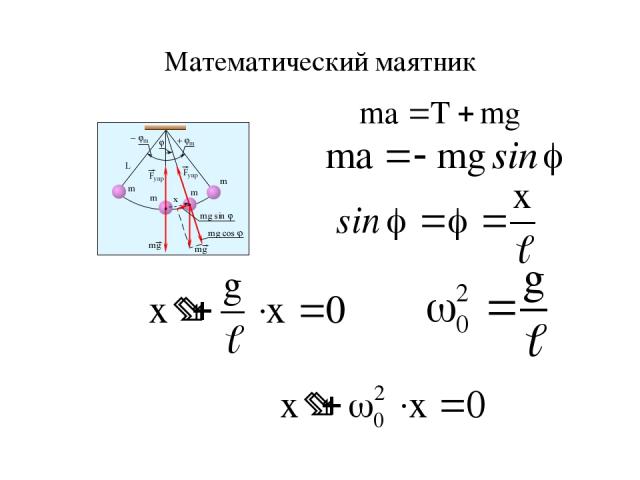
Учитывая, что момент силы тяжести и момент инерции точки из динамического уравнения вращательного движения получим:
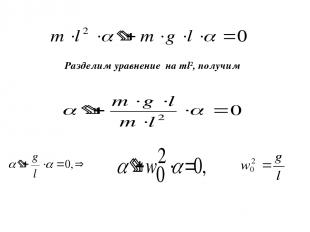
Разделим уравнение на ml2, получим

Период колебания математического маятника Мы приходим к выводу, что во всех случаях колебания описываются одним и тем же уравнением совпадающим с уравнением движения гармонического осциллятора. (18)

Вынужденные колебания. Резонанс. Автоколебания.

Вынужденными колебаниями называются незатухающие колебания системы, которые вызываются действием на неё внешних сил , периодически изменяющихся с течением времени. Сила, вызывающая вынужденные колебания, называется возмущающей (вынуждающей) силой. Вынуждающая сила изменяется по закону: F0- амплитуда вынуждающей силы, w- циклическая частота. Под действием этой силы в системе устанавливаются гармонические колебания с циклической частотой w. (19)

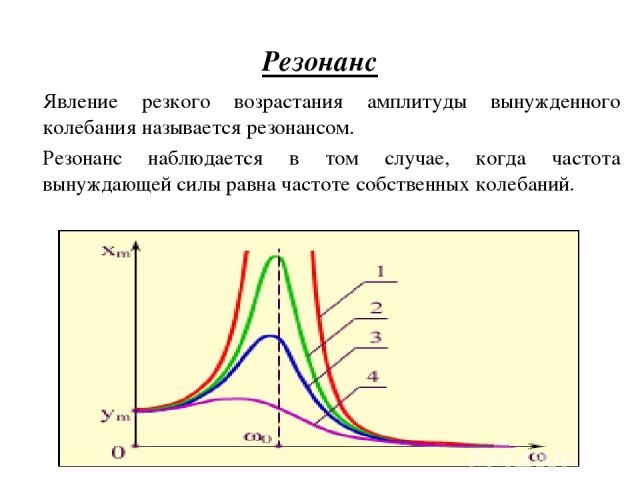
Амплитуда вынужденных колебаний зависит от амплитуды вынуждающей силы и её частоты, зависимость амплитуды колебаний от частоты приводит к тому, что при некоторой частоте амплитуда вынужденного колебания достигает максимального значения. Это явление получило название резонанса, а соответствующая частота- резонансной частоты. , то A достигнет максимального значения при частоте Где A- амплитуда вынужденных колебаний смещения. - разность фаз между вынужденными колебаниями и силой F(t).
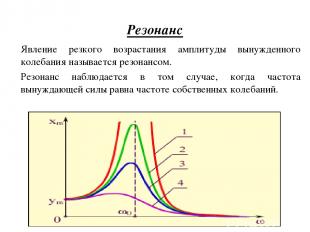
Резонанс Явление резкого возрастания амплитуды вынужденного колебания называется резонансом. Резонанс наблюдается в том случае, когда частота вынуждающей силы равна частоте собственных колебаний.

Явление возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к значению wрез – называется резонансом , wрез – резонансная циклическая частота. Явление резонанса используется в акустике- для анализа звуков, их усиления и.т.д. Под действием периодически изменяющихся нагрузок в машинах и различных сооружениях могут возникнуть явления резонанса, которые могут быть опасны для эксплуатации машин.
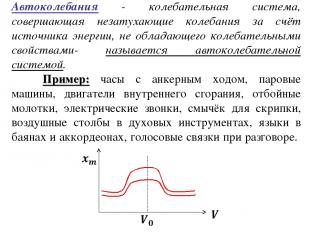
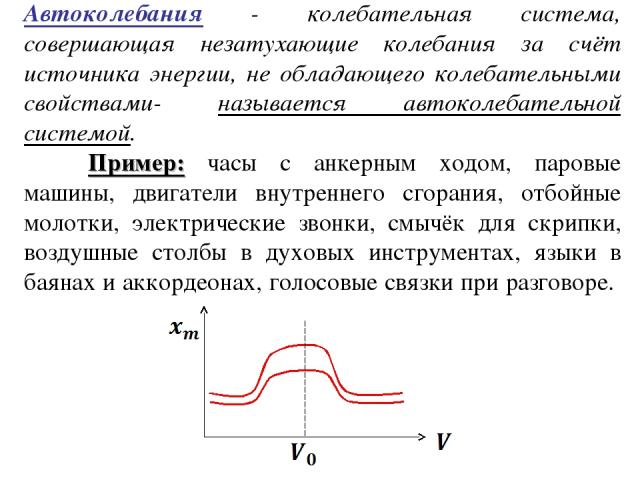
Автоколебания - колебательная система, совершающая незатухающие колебания за счёт источника энергии, не обладающего колебательными свойствами- называется автоколебательной системой. Пример: часы с анкерным ходом, паровые машины, двигатели внутреннего сгорания, отбойные молотки, электрические звонки, смычёк для скрипки, воздушные столбы в духовых инструментах, языки в баянах и аккордеонах, голосовые связки при разговоре.

Логарифмический декремент затухания

Примеры проявления резонансных явлений в живых организмах.

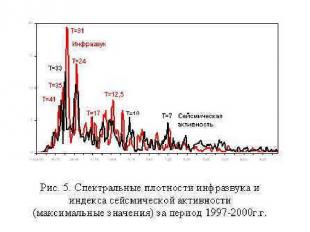
В лаборатории электроакустики в Марселе испытывали генератор, создававший акустические волны с частотой 7 Гц (инфразвук), люди испытывали сильные внутренние боли, нарушение координации движений и зрения. Оказалось, что инфразвук действует на вестибулярный аппарат, собственная частота которого 2…20 Гц; он переходит в резонансные колебания, нарушающие деятельность вестибулярного аппарата. Инфразвук также вызывает вынужденные колебания различных органов, каждый из которых обладает собственной частотой.

Некоторые из них, такие как печень, почки, сами по себе не совершают колебательных движений, но под действием внешней периодической силы могут войти с ней в резонанс. Особенно вредны резонансные явления для сердца. Это приводит к расширению кровеносных сосудов и кровоизлияниям. Если резонансные колебания находятся в противофазе, то возможны торможение кровообращения, остановка сердца.

Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение взаимно перпендикулярных колебаний.

В основе метода векторных диаграмм лежит понятие вращающегося вектора. Возьмем ось x и из точки О отложим вектор x0 под углом к оси x. Если привести вектор во вращение с угловой скоростью то проекция конца этого вектора на ось x будет перемещаться по оси x в пределах от до при этом координата будет изменяться по закону Проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора и частотой равной угловой скорости вращения , x0 x o

Сложение колебаний, происходящих вдоль одной прямой. Пусть точка совершает два колебания, происходящие вдоль одной прямой с одинаковой частотой, описываемых уравнениями: x y A A1 A2 x2 x1 Представив оба колебания в виде векторов и сложив их по правилу сложения векторов можно получить результирующее колебание. Это вектор, проекция которого на ось X равна сумме проекций исходных колебаний. Запишем результирующее колебание в виде Из рисунка и

Сложение взаимно перпендикулярных колебаний Допустим, что материальная точка будет совершать колебания в двух взаимно перпендикулярных направлениях. Если возбудить оба эти колебания, то точка будет двигаться по некоторой траектории, вид которой зависит от разности фаз складываемых колебаний. Пусть колебания заданы уравнениями: которые являются координатами движущейся точки, заданными в параметрической форме. Исключив из этих уравнений параметр t, получим уравнение траектории точки. Сделаем некоторые математические преобразования: , (2)

, , , Развернём cos в уравнение (2) по формуле для косинуса суммы: подставим вместо и их значения, получим после преобразования получим : Это уравнение эллипса. Это уравнение представляет собой общее уравнение траектории материальной точки, совершающей два взаимно перпендикулярных колебания.










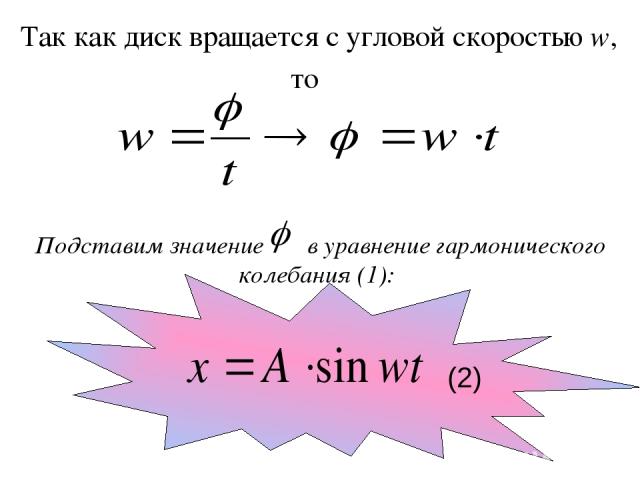

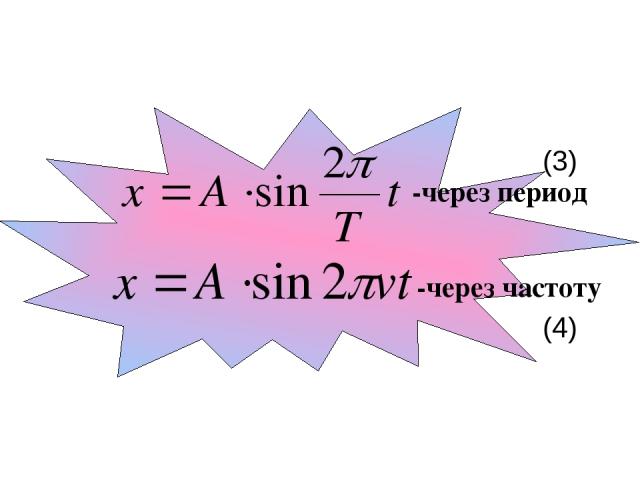

![w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени. 6. v- частота- число колебаний в единицу времени. w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5. wt- фаза колебания - характеризует состояние колебательной системы в любой заданный момент времени. 6. v- частота- число колебаний в единицу времени.](https://fs3.ppt4web.ru/images/132073/189483/640/img17.jpg)