Презентация на тему: Вязкость жидкости

ГИДРОДИНАМИКА Вязкость жидкости.Уравнение Ньютона Закон Пуазейля Число Рейнольдса Методы определения вязкости жидкости Механическая работа и мощность серца

Вязкость жидкости.Уравнение Ньютона В реальной жидкости между молекулами действуют силы взаимноного притяжения, обусловливающие внутреннее трение. Внутреннее трение, например, вызывает силу сопротивления при помешивании жидкости, замедление скорости падения брошенных в нее тел, а также определенных условиях — ламинарное течение. Ньютон установил, что сила FВ внутреннего трения между двумя слоями жидкости, движущимися с различными скоростями, вависит от природы жидкости и прямо пропорциональна площади S соприкасающихся слоев и градиенту скорости dv/dz между ними: FВ= ηSdv/dz , где η — коэффициент пропорциональности, называемый коэффициентом вязкости или просто вязкостью жидкости и зависящий от ее природы.

Сила FВ действует касательно к поверхности соприкасающихся слоев жидкости и направлена так, что ускоряет слой, движущийся более медленно, и замедляет слой, движущийся бо лее быстро. Градиент скорости в данном случае характери зует быстроту изменения скорости между слоями жидкости, т.е. в направ лении, перпеникулярном - направлению тёчения жид кости. Для конечных зна чений он равен Δν/Δz = ( ν2 − ν1) / Δz Единица коэффициента вязкости в СИ — Н·с/м², в системе СГС динс/см², эта единица называется пуазом (П). Соот ношение между ними: 1 П = 0,1 Н·с/м². На практике вязкость жидкости характеризуют относительной вязкостью ηотп, под которой понимают отношение коэффициента вязкости данной жидкости η к коэффициенту вязкости воды ηв при тон же температуре: η0TH = η/ηB (при t — 20° С ηв = 0,01 П).

У большинства жидкостей (вода, низкомолекулярные органические соединения, истинные растворы, расплавленные металлы и их соли) . коэффициент вязкости зависит только от природы жидкости и температуры (c повышением температуры коэффициент вязкости понижается). Такие жидкости называются ньютоновскими. У некоторых жидкостей, преимущественно высокомолекулярных (например, растворы полимеров) или представляющих дисперсные системы (суспензии и имульсии),коэффициент вязкости зависит также от режима течения — давдения и градиента скорости.При их увеличении вязкость жидкости уменьшается вследствие нарушения внутрен ней структуры потока жидкости. Такие жидкости называются структурно вязкими или не ньютоновскими. Их вязкость характеризуют так называемым условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, скорость).

Для более вяаких жидкостей применяется метод, основанный на измерении скорости падения в жидкости небольших тел сферической формы (метод Стокса). Стоке эмпирически установил, что при не слишком быстром движении тела сферической формы в вязкой жидкости сила FВ сопротивления движению прямо пропорциональна скорости v, радиусу r тела и коэффициенту вязкости η жидкости: FВ = 6πrηv Определение делается путем измерения скорости v падения шарика неболь шого радиуса r узком цилиндре, наполненном исследуемой жидкостью. При падении шарика, состоящего из вещества с плотностью ρ в жидкости с плотностью ρo на него действуют три силы: сила тяжести Р = (4/3)nr³ρg выталкивающая сила FА = (4/3)πr3ρ0g и сила сопротивления FB .При равномерном дви жении шарика Р = FА + FB ,откуда FB = Р — FА или 6πrηv = (4/3) πr3(ρ−ρo)g. Отсюда коэффициент вязкости жидкости

Закон Пуазейля

Математический анализ этого явления показывает, что распреде ление скоростей по сечению круглой трубы имеет параболический характер: Максимальная скорость в центре трубы В этих формулах: p1 и p2 — давления в начале и в конце участка трубы длиной l, η — коэффициент вязкости жидкости, R — радиус грубы и r — радиус рассматриваемого слоя жидкости.Градиент скорости, по абсолютной величине равный наоборот, максимален в пристеночном слое, затем постепенно уменьшается и обращается в ноль на оси трубы.

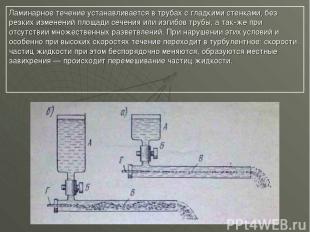
Ламинарное течение устанавливается в трубах с гладкими стенками, без резких изменений площади сечения или изгибов трубы, а так же при отсутствии множественных разветвлений. При нарушении этих условий и особенно при высоких скоростях течение переходит в турбулентное: скорости частиц жидкости при этом беспорядочно меняются, образуются местные завихрения — происходит перемешивание частиц жидкости.

Это можно наблюдать на следующем опыте (рис.). В стеклянную трубку В, соединенную с наполненным водой резервуаром А, с торца вставлен стержень Г из легкорастворяющейся краски, от которого в об щий поток воды поступает окрашенная струйка. Скорость течения воды регулируется краном Б. При небольшой скорости течения окрашенная струйка не смешивается с основным потоком (рис. а) — течение ламинарное. При повышении скорости течения воды окрашенная струйка начинает колебаться, теряет резкую границу, образует завихрения и при еще большей скорости разрывается на части и смешивается с общим потоком (рис. б) — течение становится турбулентным. Характерным для турбулентного течения являются местные изменения давления в жидкости, вызывающие колебательное движние частиц, сопровождающееся звуковыми явлениями (шум, журчание и т.п.), благодаря которым турбулентное течение легко обнаруживается.

Пуазеиль опытным путем уста новил, что средняя скорость Vср ламинарного течения жидкости по неширокой горизонтальной круглой трубе постоянного сечения прямо пропорциональна разности давлений р1 и р2 при входе и выходе из трубы, квадрату радиуса R трубы и обратно пропорциональна длине l трубы и коэффициенту вязкости η жидкости (закон Пуазейля ): Средняя скорость Vср течения жидкости определяет количество жидкости Q, протекающее через поперечное сечение S трубы в единицу времени: Q = VсрS, где S = πR². Следовательно,

Число Рейнольдса Скорость Vкр перехода ламинарного течения в турбулентное можно определить, пользуясь определенным из опыта критерием — числом Рейнольдса Re (безразмерная величина), которое связывает ее с плотностью ρ, вязкостью η жидкости и диаметром D трубы: Re = vкp ρD\η. Для прямой гладкой трубы ReKp = 2300. Если Re ≥ ReKp, то течение переходит в турбулентное. Число Рейнольдса является критерием подобия. При моделиро-вании гидро- и аэродинамических систем, в частности кровенос-ной системы, модель должна иметь такое же число Рейнольдса, как и натура, в противном случае не будет соответствия между ними. Это относится также и к моделированию обтекания тел при движении их в жидкости или газе.

Методы определения вязкости жидкости

Таким же образом можно измерить tx — время протекания такого же объема исследуемой жидкости., Для того, чтобы по формуле найти коэффициент внутреннего трения исследуемой жидкости ηх, нужно знать разности давлений ∆рx и ∆р0. Величина ∆р в вискозиметре зависит от разности уровней жидкости в коленах вискозиметра: ∆p = ρhg где ρ — плотность жидкости, a h — разность уровней жидкости в, коленах вискозиметра. При одинаковых разностях уровней h исследуемой и эталонной жидкостей, отношение давлении равно отношению плотностей этих жидкостей. Величина ∆р уменьшается по мере вытекания жидкости, но отношение разностей давлений при равных условиях остается постоянным. Поэтому формулу можно написать следующим образом: ηx=η0

Плотность исследуемой жидкости рх можно измерить с по мощью ареометра. В качестве эталонной жидкости обычно берется вода. Ее плотность р0 и коэффициент внутреннего трения находят по таблицам. Так как коэффициент внутреннего трения сильно зависит от температуры, измрения производят в условиях термостатирования. Для этого помещают вискозиметр в банку с водой, которая является термостатом.

ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ ЖИДКОСТИ ПО МЕТОДУ ПАДАЮЩЕГО ШАРИКА. Этот метод широко применяется для определения коэф фициента внутреннего трения сильно вязких жидкостей, таких как глицерин и различные масла. Недостатком этого метода является то, что он требует значительного количества исследуемой жидкости. При движении шарика в вязкой жидкости возникает сила трения, величина которой зависит от коэффициента внутреннего трения жидкости. Формула для вычисления этой силы была выведена Стоксом, поэтому данный метод часто называют методом Стокса. На шарик, падающий в вязкой жидкости, действуют три силы: 1. Направленная вниз сила тяжести P = mg= πr3ρg где r — радиус шарика, а ρ — плотность вещества, из которого сделан шарик. 2. Направленная вверх выталкивающая сила (архимедова сила), равная весу жидкости в объеме шарика Fвыт=m1g= πr3ρжg Где r — радиус шарика, а ρж — плотность жидкости.

3. Сила трения FTp. Эта сила также направлена вверх, а ее численное значение находится по формуле Стокса Fтр = 6πгηυ, где r — радиус шарика, η— коэффициент внутреннего трения жидкости, a v— скорость движения шарика. Формула Стокса. справедлива только для маленьких шариков, движущихся с небольшой скоростью. При увеличении размеров шариков и при возрастании скорости их движения возможно образование завихрений. В этом случае сила трения стано вится пропорциональной более высокой степени, скорости. При движении шарика силы Р и Fвыт все время остаются постоянными, а сила трения возрастает по мере увеличения скорости. В начале движения сила Fтр очень Мала и шарик движется ускоренно под действием силы, равной Р - Fвыт - Fтр С увеличением скорости уве личивается и сила Fтр и наступает такой момент, что направленные вверх силы Fтр и Fвыт уравновесят направленную вниз силу тяжести Р: P=Fвыт + Fтр

Механическая работа и мощность серца

Особенностью данной системы является прежде всего постепенное и множественное разветвление трубок, особенно в ее средней части. Последняя состоит из весьма большого числа коротких параллельных трубок малого сечения, общий просвет которых имеет настолько большое сечение, что скорость жидкости здесь снижается почти до нуля. Однако внутреннее трение в пристеночных слоях этих трубок настолько велико, что именно эта средняя часть системы представляет наибольшее сопротивление течению жидкости и обусловливает максимальное падение давления. Другой особенностью системы является эластичность стенок тру бок, благодаря которой при ритмической работе насоса ток жидкости в ней принимает равномерный характер. Допустим, что при сжатии груши некоторое количество жидкости поступает в трубку А, уже за полненную жидкостью под некоторым давлением. Давление в трубке А повышается, эластичные стенки ее растягиваются и вмещают избыток жидкости (рис. 33, б). Затем стенки трубки А постепенно сокращаются и прогоняют избыток жидкости в следующее звено системы, стенки ко торого также сначала растягиваются , затем сокращаются и таким образом проталкивают жидкость в последующие звенья системы трубок. В результате течение жидкости постепенно принимает равномерный характер.

Переходим к сосудистой системе. Начальное давление, необходимое для продвижения крови по всей сосудистой системе, создается работой сердца. Рассмотрим схематически явления, происходящие в большом кpугe кровообращения. При каждом сокращении левого желудочка сердца в аорту, уже заполненную кровью под соответствующим давлением, выталкивается так называемый ударный объем крови, в среднем рав ный 65—70 мл. Затем клапаны аорты закрываются. Поступивший в аорту дополнительный объем крови повышает давление в ней и соответственно растягивает ее стенки. Волна повышенно го давления, которое называется систолическим, вызывает колебания сосудистых стенок, распространяющиеся вдоль более крупных артерий в виде упругой волны. Эта волна давления называется пульсовой волной, скорость ёе распространения зависит от упругости сосудистых стенок и имеет порядок 6—8 м/с. Затем в период расслабления сердечной мышцы (диастола) стенки аорты постепенно сокращаются до исходного положения и проталкивают поступивший объем крови в более дистальные крупные артерии. Стенки последних в свою очередь растягиваются и затем, сокращаясь, протак- ливают кровь в последующие звенья сосудистой системы. В ре зультате ток крови принимает непрерывный характер со скоростью в крупных сосудах порядка 0,3—0,5 м/с.

Кровь представляет собой суспензию форменных элементов в белковом растворе — плазме. Поэтому, строго говоря, она должна быть отнесена к неньютоновским жидкостям. Кроме того, при течении кро ви по сосудам наблюдается концентрация форменных элементов в цент ральной части потока, где вязкость еоответственно увеличивается. Но поскольку вязкость крови не так велика, этими явлениями пренебре гают и считают ее коэффициент вязкости постоянной вели-чиной. Относительная вязкость крови в норме составляет 4,2—6. При патоло гических условиях она может снижаться до 2—3 (при анемии) или повышаться до 15—20 (при полицитемии). Относительная вязкость сыво ротки крови в норме 1,64—1,69 и при патологии 1,5—2,0. При инфекционных заболевании вязкость увеличивается. При брюшной тиф, туберкулезе уменьшается вязкость. Веночная кровь обладает более вязкость чем артерии.

Работа, совершаемая сердцем, затрачивается на преодоление сил давления и сообщение крови кинетической энергии. Рассчитаем работу, совершаемую при однократном сокращении левого желудочка. Изобразим ударный объем крови Vу в виде цилиндра. Можно считать, что сердце продавливает этот объем по аорте сечением S на расстояние l при среднем давлении p. Совершаемаяпри этом работа На сообщение кинетической энергии этому объему крови затрачена Работа где ρ — пдотность крови, V — скорость крови в аорте. Такимобразом, Работа левого желудочка сердца при сокращении равна Так как работа правого желудочка принимается равной 0,2 от работы левого, то работа всего сердца при однократном сокращении