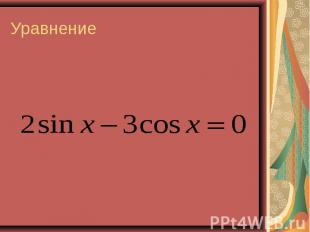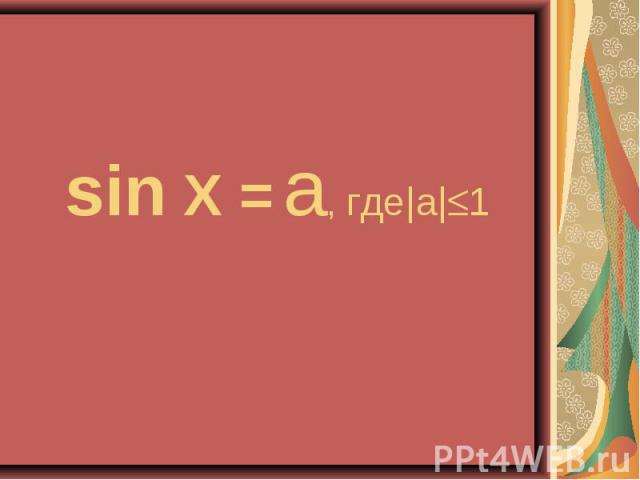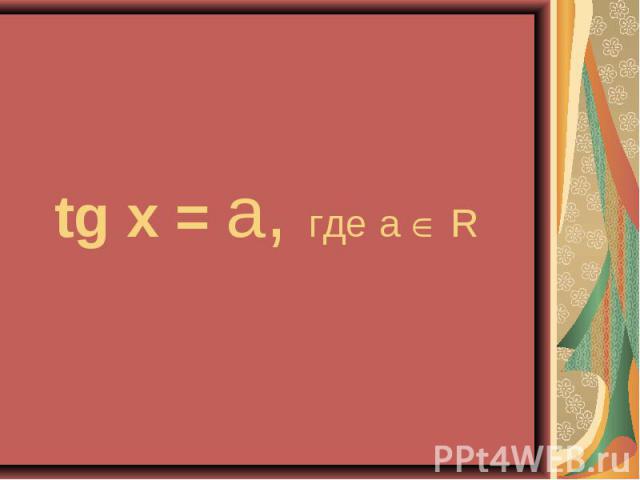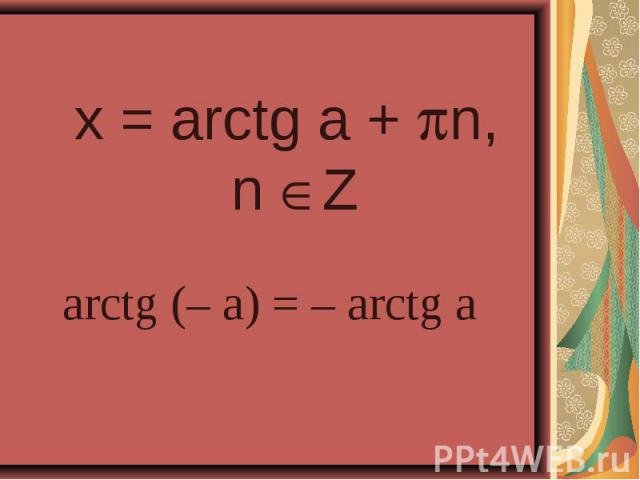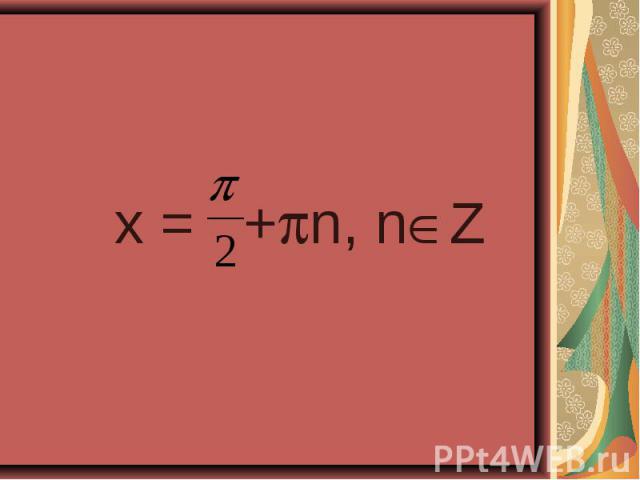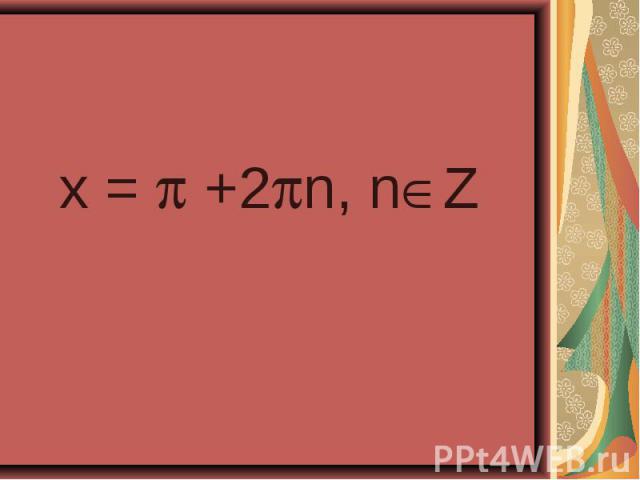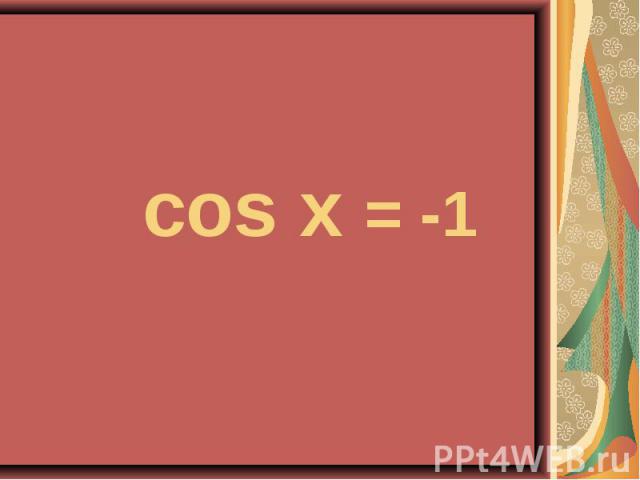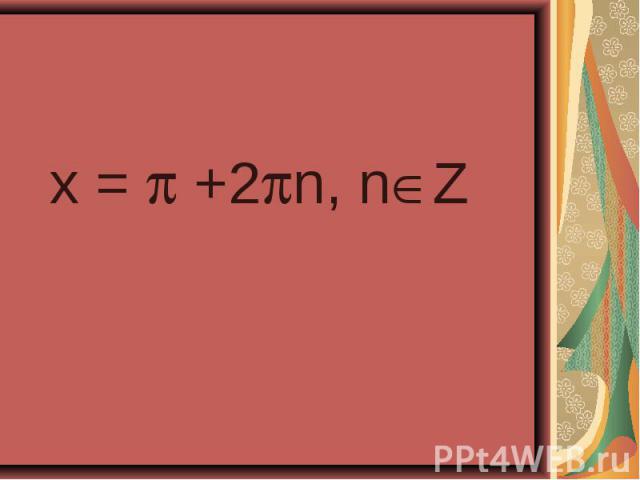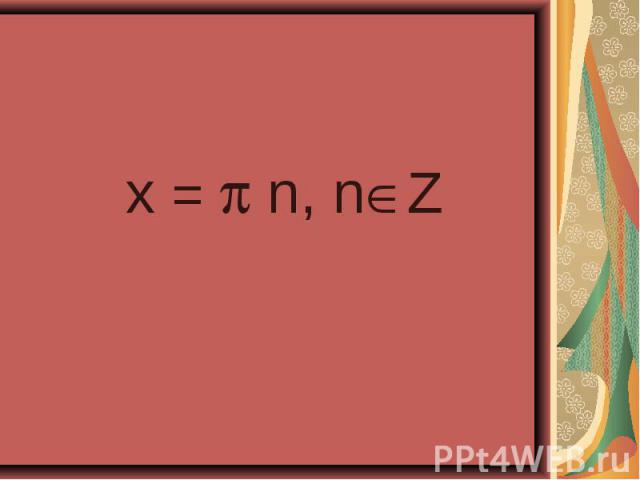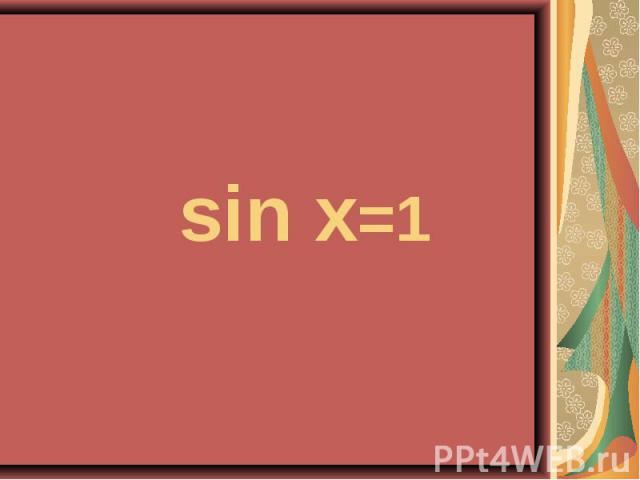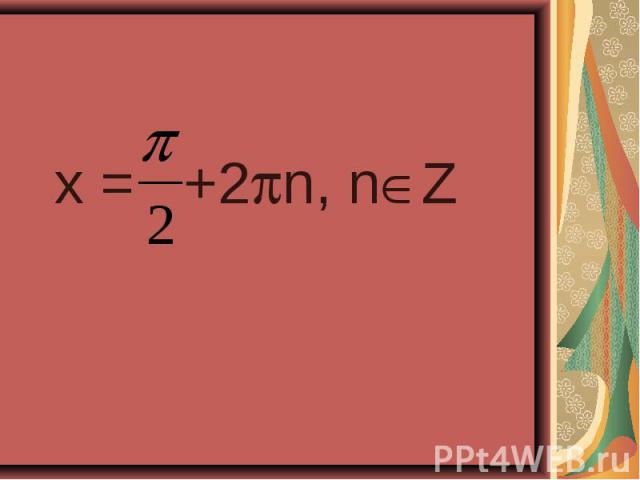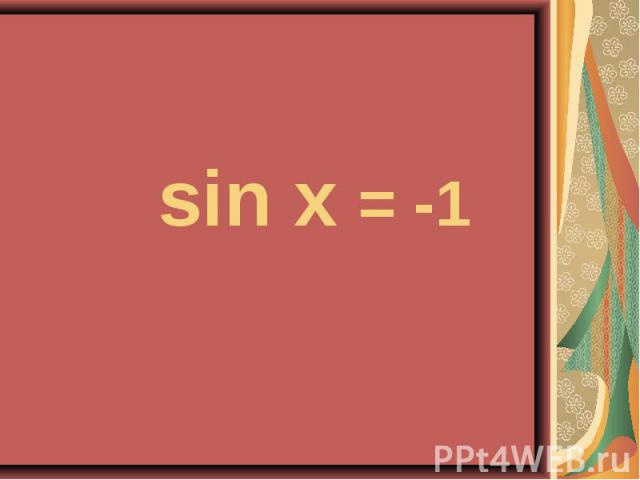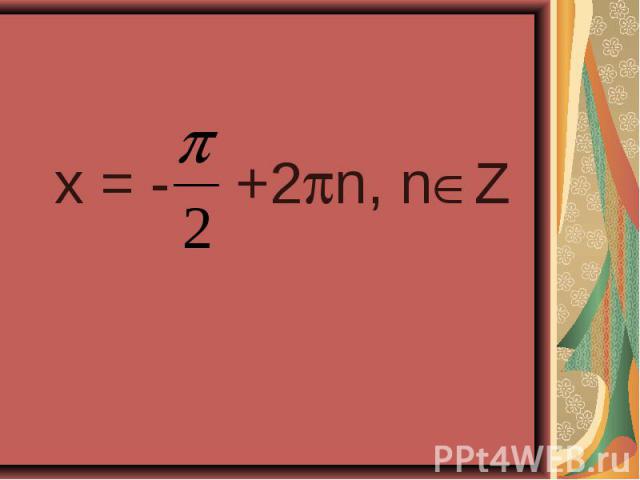Презентация на тему: Решение тригонометрических уравнений


Создания условий для осознанного усвоения решения тригонометрических уравнений вида Создания условий для осознанного усвоения решения тригонометрических уравнений вида a sinx + b cosx = c. Формирование навыков самоконтроля и взаимоконтроля, алгоритмической культуры учащихся. Развитие устной математической речи. Обеспечение условий для развития умения решать тригонометрические уравнения, совершенствовать мыслительные умения старшеклассников: сравнивать, обобщать и анализировать, развития навыков обработки информации. Развитие коммуникативных умений делового общения сверстников. Воспитание аккуратности.


sin7x – sin x =cos4x, 2sin3x cos4x - cos4x =0, сos4x ( 2sin3x – 1 )=0, сos4x=0 или 2cos3x -1 =0 сos4x=0 4x =П/2+Пn, n € Z; cos3x =1/2, X=П/8 +Пn/4, n € Z, 3x =±аrccos1/2 +2Пn, n 3x =±П/3 +2Пn, n € Z, X =±П/9 + 2/3Пn, n € Z. Ответ: X=П/8 +Пn/4, X =±П/9 = 2/3Пn, n € Z

sin²x - cos²x = cos4x sin²x - cos²x = cos4x

sin²x-cos²x =cos4x , sin²x-cos²x =cos4x , - (cos² - sin²x )=cos4x , -cos2x = cos²2x - sin²2x, -cos2x = cos²2x – ( 1 - cos²2x), -cos2x - cos²2x +1 - cos²2x = 0, -2cos²2x – cos2x +1 = 0, 2cos²2x + cos2x -1 = 0. Заменим сos2x на У , где |У| 1 Тогда 2 у² +у -1 = 0, D =1 - 4•2•(-1) =9, У =1/ 2, у = -1. Выполним обратную замену Cos2x =1/ 2 , cos2x = -1, 2x = П+2Пn, n € Z, 2x =±arccos1/2 =2Пn , n € Z, x=П/2+Пn, n € Z. 2x ±П/3 +2Пn. n € Z, X =±П/6+Пn, n € Z. Ответ: X =±П/6+Пn, x=П/2+Пn, n € Z.

№628 (1) №628 (1) №628 (3) №629 (2)



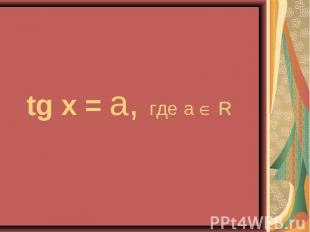
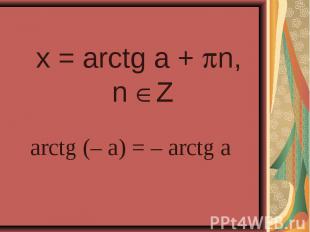
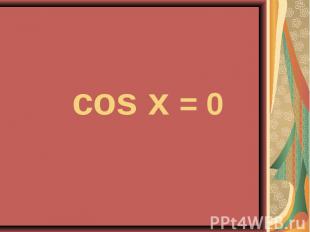
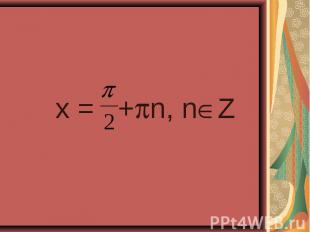

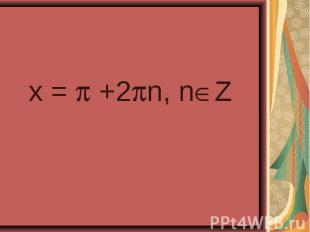
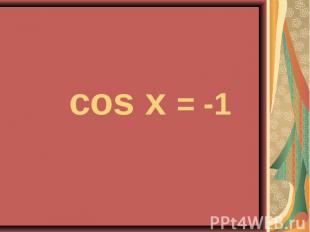
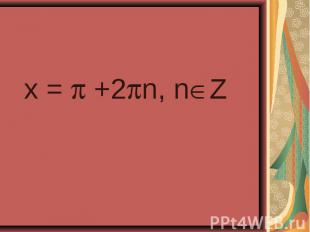
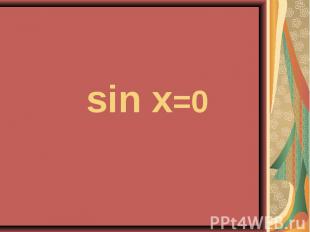
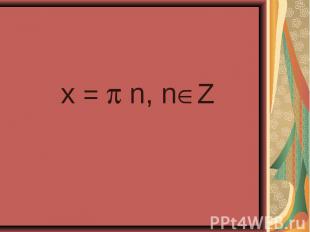
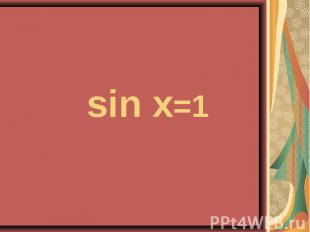
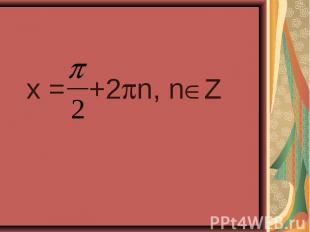
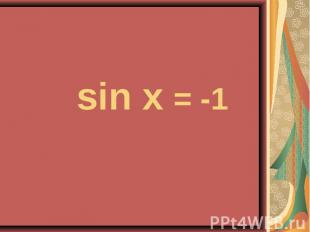
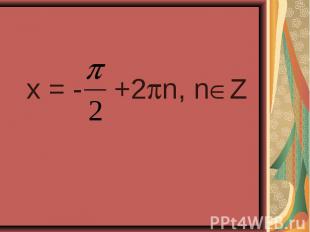

4sin²x – 4sinx – 3 = 0 4sin²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0

4sin²x - 4 sinx – 3 = 0 4sin²x - 4 sinx – 3 = 0 ( -1)n+1 П/6 +Пn, n Z. 2 сos²x – sin x – 1 = 0 ±П/6 +Пn; -П/2+2Пn, n Z.