Презентация на тему: Множество и его элементы

Работа ученицы 10-б класса Аблицовой Алены Урок математики в 10 классе

«Множество есть многое, мыслимое нами как единое». Основоположник теории множеств немецкий математик Георг Кантор (1845-1918)

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством. Примеры множеств: множество учащихся в данной аудитории; множество людей, живущих на нашей планете в данный момент времени; множество точек данной геометрической фигуры; множество чётных чисел; множество корней уравнения х2-5х+6=0; множество действительных корней уравнения х2+9=0;

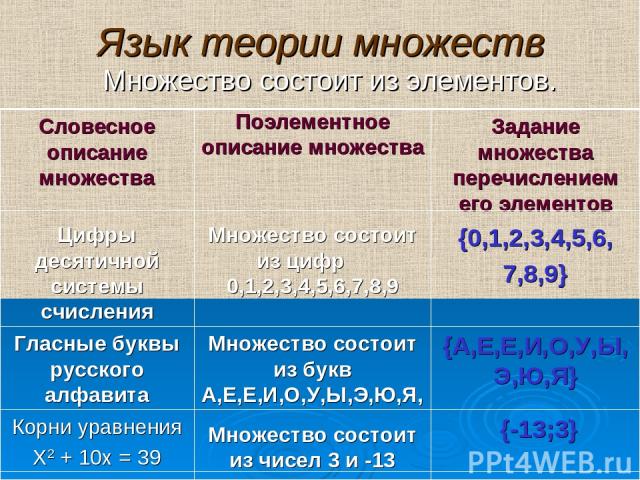
Язык теории множеств Множество состоит из элементов. {-13;3} Множество состоит из чисел 3 и -13 Корни уравнения Х2 + 10х = 39 {А,Е,Е,И,О,У,Ы,Э,Ю,Я} Множество состоит из букв А,Е,Е,И,О,У,Ы,Э,Ю,Я, Гласные буквы русского алфавита {0,1,2,3,4,5,6, 7,8,9} Множество состоит из цифр 0,1,2,3,4,5,6,7,8,9 Цифры десятичной системы счисления Задание множества перечислением его элементов Поэлементное описание множества Словесное описание множества

Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Для числовых множеств применяют перечисление от меньшего числа к большему числу. Пустое множество т.е. множество, не содержащее ни одного элемента. Обозначается Ø

Множество всех чисел, которые больше 2 и меньше 7 (2; 7) 6 Множество всех чисел, которые больше 2 и меньше 7 {х│2 < х < 7} 5 Множество рациональных чисел Q 4 Множество натуральных чисел N 3 Множество всех квадратов натуральных чисел {1,4, 9,16 25,49, ...} 2 Множество всех двузначных чисел, кратных пяти {10,15,20, ..., 90,95} 1 Словесное описание множества Задание множества

Задание множества с помощью характеристического свойства {х│2 < х

Элемент х принадлежит множеству А х является элементом множества А Элемент х не принадлежит множеству А х не является элементом множества А

Подмножества Элементы, образующие данное множество А, можно объединять не сразу все вместе, а группируя их в разных комбинациях. Так можно получать подмножества данного множества. Пример: А – множество всех учеников девятого класса В – множество девочек этого девятого класса С – множество мальчиков этого девятого класса В и С – подмножества множества А

Определение: Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А. Обозначение Знак называют знаком включения

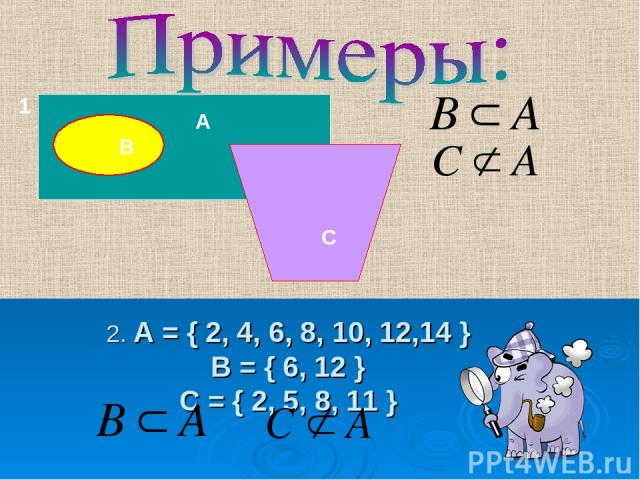
2. А = { 2, 4, 6, 8, 10, 12,14 } В = { 6, 12 } С = { 2, 5, 8, 11 } А В С 1.

№531(а, б) Множество задано словесным описанием. Задайте это множество, перечислив его элементы: а) цифры, которые больше ; б) целые отрицательные числа, которые больше - .

№ 532 (а, в, г) Множество задано перечислением своих элементов. Приведите какое-нибудь его словесное описание: а) {0, 2, 4, 6, 8} в) {3, 6, 9, ..., 27, 30} г) {A, B, C, D, X, Y, Z}

№ 536(а) Верно ли, что: 0,7 {х│х2 - 1< 0} № 538 Дано множество { -8,1; √2; 17/7}. Перечислите все его подмножества, состоящие из двух чисел: а)разного знака б)положительных в)рациональных г)среди которых есть иррациональное число

№ 541 На числовой прямой изобразите следующие промежутки: А = (-√2; 1), В = [0; 1,9), С = [-1,5; 200/101]. Верно ли, что: а) б) с) г)

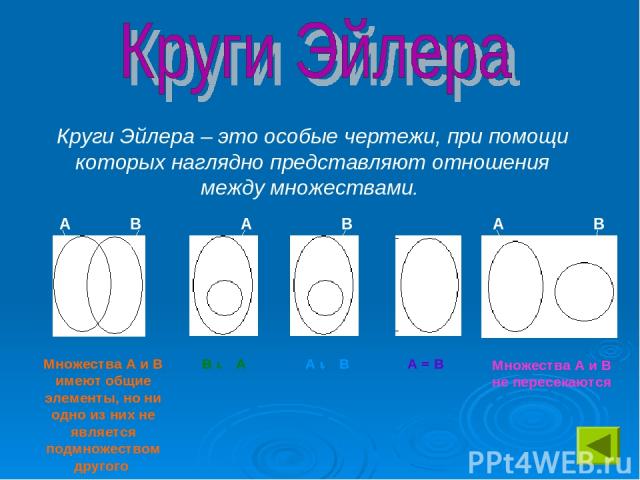
Изображение множеств в виде плоских фигур очень удобно для наглядного объяснения различных операций над множествами. Обычно множества изображают в виде кругов. Такие круги называют кругами Эйлера.

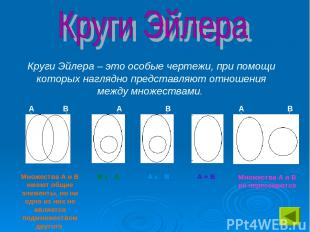
Круги Эйлера – это особые чертежи, при помощи которых наглядно представляют отношения между множествами. Множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого В М А А М В А = В Множества А и В не пересекаются А В А А А В В В А=В В

Определение: Пересечением множеств А и В называют множество, состоящее из всех общих элементов множеств А и В, т.е. из всех элементов, которые принадлежат и множеству А, и множеству В Обозначение: А ∩ В Запись: А ∩ В = {х│х А и х В }

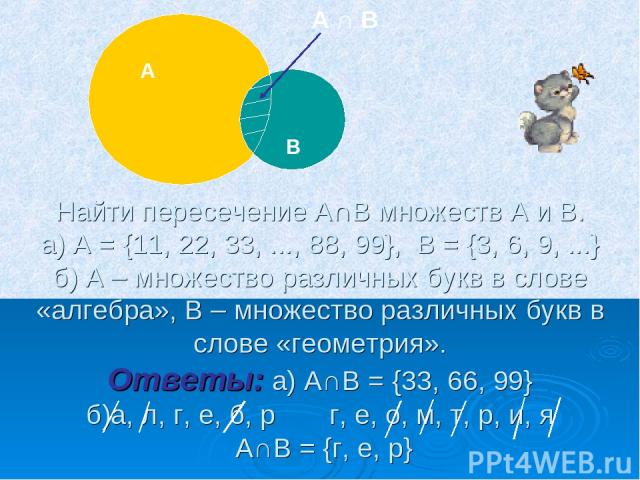
Найти пересечение А∩В множеств А и В. а) А = {11, 22, 33, ..., 88, 99}, В = {3, 6, 9, ...} б) А – множество различных букв в слове «алгебра», В – множество различных букв в слове «геометрия». Ответы: а) А∩В = {33, 66, 99} б)а, л, г, е, б, р г, е, о, м, т, р, и, я А∩В = {г, е, р} А В А ∩ В

Решение систем уравнений, систем неравенств – это примеры пересечений различных множеств. f(x) = 0 g(x) = 0 f(x) >0 g(x) >0

Определение: Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В. Обозначение: А U В Запись: АUВ = {х│х А или х В}

Найти объединение АUВ множеств А и В. а) А – множество делителей числа 105, В – множество делителей числа 55 Решение: А = {1, 3, 5, 7, 15, 21, 35, 105} В = {1, 5, 11, 55} АUВ = {1, 3, 5, 7, 11, 15, 21, 35, 55, 105} А В А U В

№ 542(а, в) Найдите пересечение А∩В множеств А и В. а)А = {10,20,30, ...}, В = {1 2,3, ...,41} в)А = {-11,-10,-9, ...,-1,0,1,...9}, В – целые числа, кратные 10.

№ 543 - 544(а, г) Даны числовые промежутки: А = (0; 1), В = [-0,5; 0,9], С = [-1; 1], D = (0,1; 1,1]. Изобразите на числовой прямой множества: а)А ∩ В; г)А ∩ В ∩ С ∩ D а)А U В; г)А U ВU С U D

№ 545 Даны множества: А = {a,b,c,d}, В = {c,d,e,f}, С = {с,e,g,k}. Найдите множество: а) (А ∩ В) ∩ С б) (А ∩ В) U С в) (А U В) ∩ С г) (А U В) U С