Презентация на тему: Методы решения уравнений и неравенств

Научный руководитель: Иноземцева Елена Ивановна Нестандартные методы решения уравнений и неравенств Боков Иван Куркова Анастасия Малашок Полина Матющенко Роман Мхитарян Артем Подцикина Серафима Подцыкин Максим Шпилева Надежда 2010 г. МНОУ «Лицей» 900igr.net

Гипотеза работы Существует большое количество способов решения уравнений и неравенств, многие из которых не изучаются согласно школьной программе

Цели работы Изучить нестандартные методы решения уравнений и неравенств Научиться использовать их на практике Создать наглядную и понятную презентацию для ознакомительных целей Ознакомить класс с этими методами при помощи наглядных примеров Создать папку с материалами работы

Древний Египет «Фальфивое правило» Задача: куча. Ее седьмая часть 19. Найти кучу Будет хорошо

Вавилон Диофант (жил предположительно в III веке н. э.) Квадратные уравнения Задача: Найти два числа, зная, что их сумма равна 20, а произведение — 96 x = 2 = 12 и = 8

Задача № 80 Задача: Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат Решение: s2 + 2s + 1 = (s + 1)2, (2s + I)2 + s , 4s2 + 5s + 1 = t2 , Положим, что: t = 2s — 2 , t2 = 4s2 — 8s + 4 = 4s2 + 5s + 1, 4s2 — 8s + 4 = 4s2 + 5s + 1. Проверка:

Кубические уравнения Архимед (287 до н. э. — 212 до н. э.) Сочинение: «О шаре и цилиндре» Задача: рассечь заданный отрезок а на две части х и а—х так, чтобы (а — х) : с = S : х2

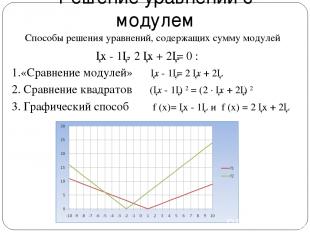
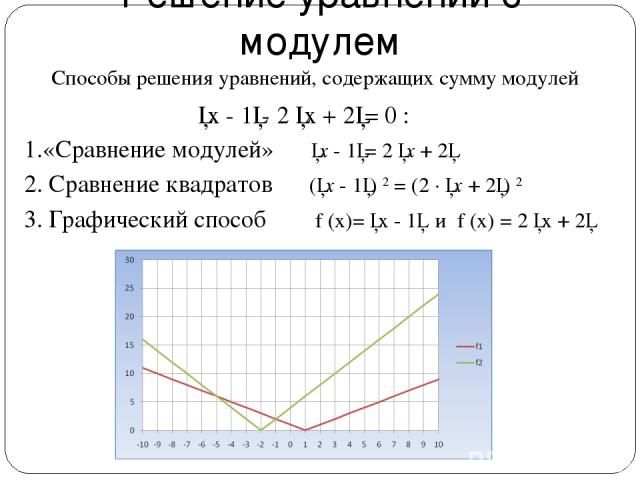
Решение уравнений с модулем 1.«Сравнение модулей» │x - 1│= 2 │x + 2│ 2. Сравнение квадратов (│x - 1│) 2 = (2 ∙ │x + 2│) 2 3. Графический способ f (x)= │x - 1│ и f (x) = 2 │x + 2│ Способы решения уравнений, содержащих сумму модулей │x - 1│- 2 │x + 2│= 0 :

Сравнение квадратов │x - 1│= 2 │x + 2│ (│x - 1│) 2 = (2 ∙ │x + 2│) 2 (х – 1) 2 - ( 2х + 4) 2 = 0 ((х – 1) - ( 2х + 4)) ∙ ((х – 1) + ( 2х + 4)) = 0 (х – 1 - 2х - 4) ∙ (х – 1 + 2х + 4) = 0 х – 1 - 2х – 4 = 0 или х – 1 + 2х + 4 = 0 - х - 5 = 0 3х + 3 = 0 x = - 5 x = - 1 Пример: Ответ:-5;-1

Введение новой переменной + раскрытие модуля на интервалах │4 |x |+ 5│= 6|x | | x |= a, где a > 0, тогда | 4а+5 |=6а 4а+5 =-6а 4а+5 =6а Не удовлетворяет условию а>0 , значит, Ответ: Пример:

Раскрытие модуля на интервалах ( начиная с внутреннего) На промежутке На промежутке Не удовлетворяет условию Не удовлетворяет условию │4 |x |+ 5│= 6|x | Пример: Ответ:

Использование свойства четности у=│4 |x |+ 5│= 6|x | . 4х + 5 = 6х и 4х + 5 = - 6х Пример: Ответ:

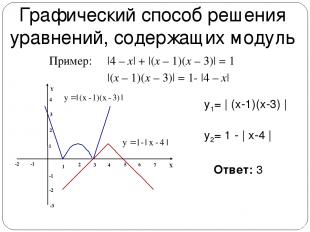
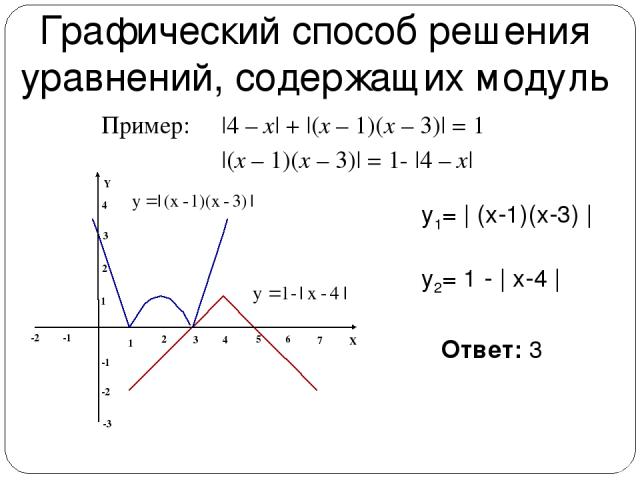
Графический способ решения уравнений, содержащих модуль |4 – x| + |(x – 1)(x – 3)| = 1 Ответ: 3 y1= | (x-1)(x-3) | y2= 1 - | x-4 | |(x – 1)(x – 3)| = 1- |4 – x| Пример:

Уравнения с параметрами Уравнение с параметрами – математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров. Способы решения: Графический Аналитический

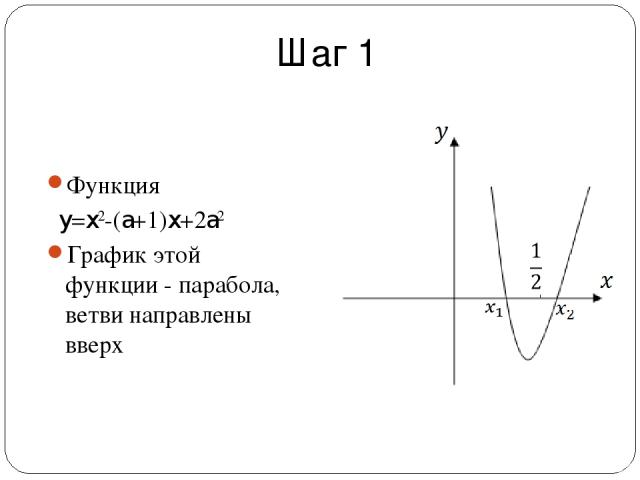
Задача: При каких значениях a один корень квадратного уравнения x2-(a+1)x+2a2=0 больше , а другой меньше ?

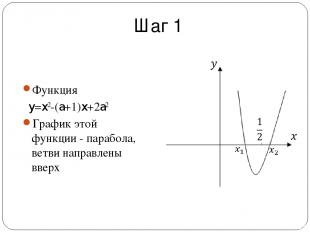
Шаг 1 Функция y=x2-(a+1)x+2a2 График этой функции - парабола, ветви направлены вверх

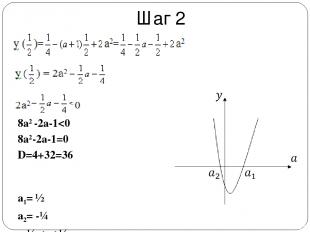
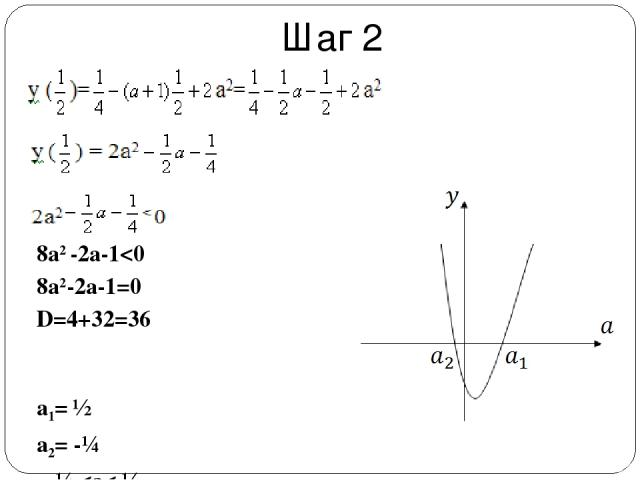
Шаг 2 8a2 -2a-1

Задача: При каких значениях b система имеет единственное решение? ; ,

1 способ , , ; ;

2 способ График первого уравнения - окружность с центром в начале координат и радиусом 3. График второго уравнения - прямая F , ;

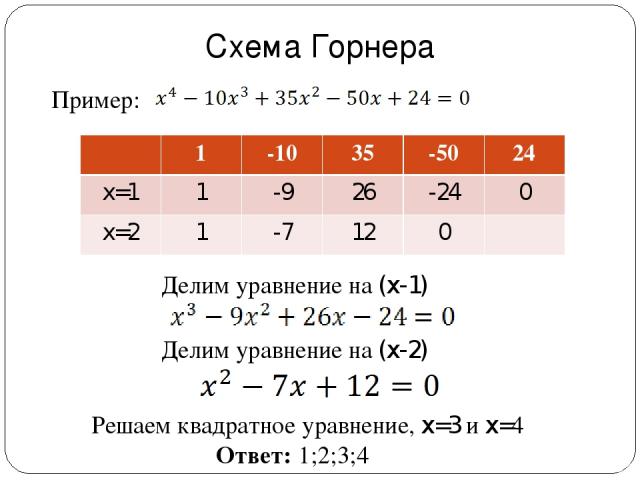
Схема Горнера Делим уравнение на (x-1) Пример: Делим уравнение на (x-2) Решаем квадратное уравнение, x=3 и x=4 Ответ: 1;2;3;4 1 -10 35 50 24 1 -10 35 50 24 x=1 1 -9 26 -24 0 1 -10 35 -50 24 x=1 1 -9 26 -24 0 x=2 1 -7 12 0

Формулы Виета Найти кубическое уравнение, корни которого являются квадратами корней уравнения Обозначим корни искомого кубического уравнения как Ответ: Задача:

Решение с выделением полного квадрата Пример: x4 – 2x3  – 3x2 + 4x + 4 = 0. Представим – 3x2 как (x2  – 4x2) x4 – 2x3 + x2  – 4x2 + 4x + 4 = 0 Свернем по формуле и вынесем общий множитель (x2  – x)2 – 4(x2 – x)  + 4 = 0 Введем замену y = (x2  – x) Решим уравнение, y=2 2= (x2  – x) x=-1 или x=2 Ответ: -1;2

Разделим обе части уравнения на ; или Ответ: Пусть , тогда получим корней нет Идея однородности Пример: ,

Решение уравнений относительно коэффициентов или ; Определяем коэффициенты и решаем квадратное уравнение: ; ; Пример: +

Ответ: 2 квадратных уравнения; корней нет; - посторонний корень

Ответ: Метод разложения на простейшие дроби Выделяем из числителя 1 и переносим:

Неравенство треугольника (Евклидова геометрия) Внешний угол больше внутреннего, с ним не смежного Против большей стороны лежит больший внутренний угол Против большего внутреннего угла лежит большая сторона

Неравенство Коши

Из всех равновеликих треугольников найти треугольник наименьшего периметра. Пусть x, y, z– стороны треугольника, тогда: Применим неравенство Коши: Наименьшее значение периметра равно Достигается при x=y=z Задача:

Неравенства с модулем Соотношение двух величин, одна из который имеет модуль, показывающее, что одна величина больше или меньше другой. Методы решения: Метод промежутков Графический

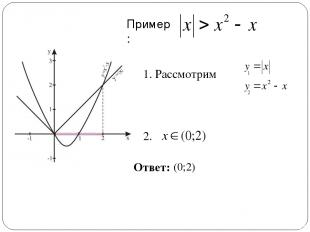
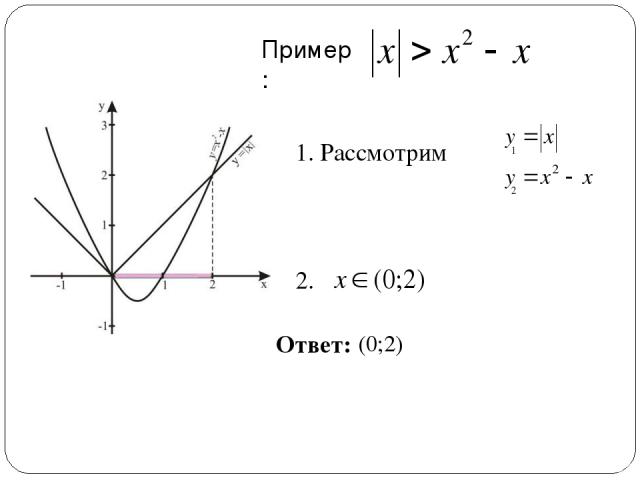
Пример: 1. Рассмотрим 2. Ответ: 1 2

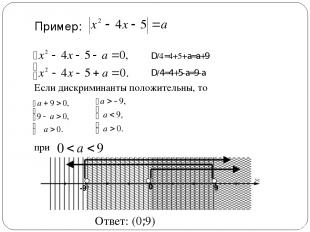
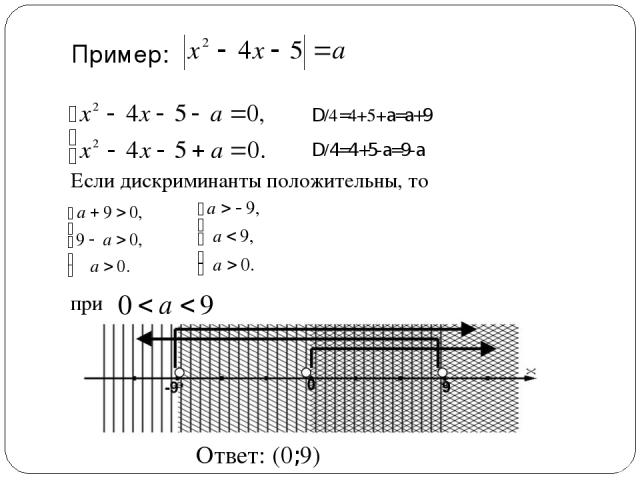
Пример: Если дискриминанты положительны, то при D/4=4+5+a=a+9 D/4=4+5-a=9-a Ответ: (0;9)

Пример: Ответ: |3х - 1| - |х - 1|< 10 1 3 1 1 х x = 0; -(3х - 1) + (х - 1)

Неравенства с параметрами Неравенство f (a,b,c,…k,x) > ϕ (a,b,c,…k,x), где a,b,c,…k – параметры, а x –действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.

Пример:   Ответ: Для всех допустимых значений параметра а решить неравенство: ; ; ; ; ;

Задача: Найдите все значения а при которых неравенство не имеет решений Ответ: (1;5) График – парабола, ветви вверх

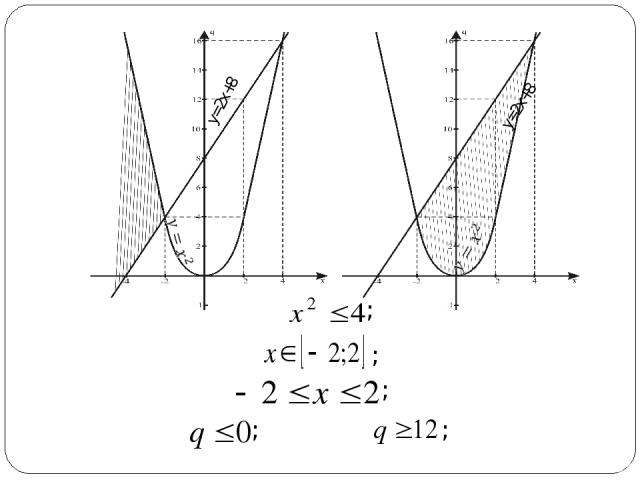
Найти все значение параметра q, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства Задача:

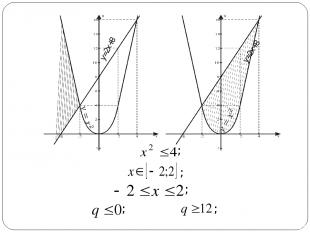
y=2x+8 y=2x+8 ; ; ; ; ;

Ответ: при исходное неравенство не содержит ни одного решения неравенства

Метод “Ромашки” f(х) = -натуральные числа f(х) >0 (соответственно

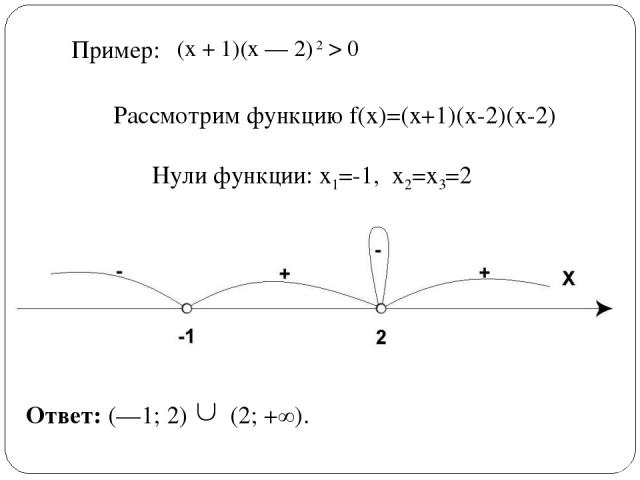
(х + 1)(х — 2) 2 > 0 Пример: Ответ: (—1; 2) (2; +∞). Рассмотрим функцию f(x)=(x+1)(x-2)(x-2) Нули функции: х1=-1, х2=х3=2

≥0 Пример: Ответ: (0; 3] {7}. Рассмотрим функцию f(x)= х≠0. х≠4 Нули функции: х=3, х=7

Заключение Мы поставили перед собой задачи: Изучить нестандартные методы решения уравнений и неравенств Научиться использовать их на практике Создать наглядную и понятную презентацию для ознакомительных целей Ознакомить класс с этими методами при помощи наглядных примеров Создать папку с материалами работы Считаем, что намеченные нами цели достигнуты.

Спасибо за внимание!