Презентация на тему: «Метод математической индукции»

Презентация по математике на тему: «Метод математической индукции»

В основе математического исследования лежит

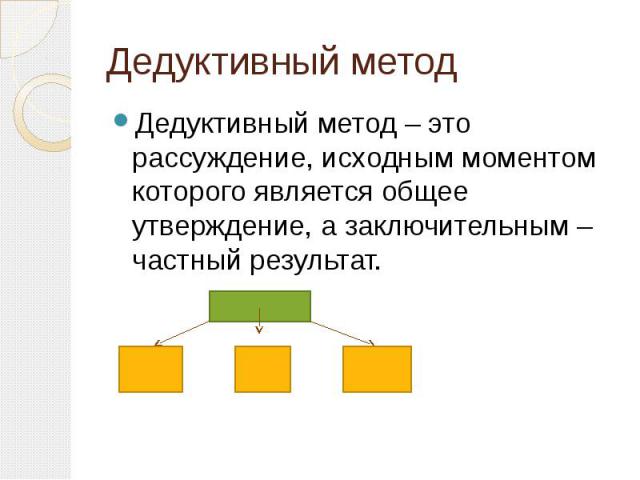
Дедуктивный метод Дедуктивный метод – это рассуждение, исходным моментом которого является общее утверждение, а заключительным – частный результат.

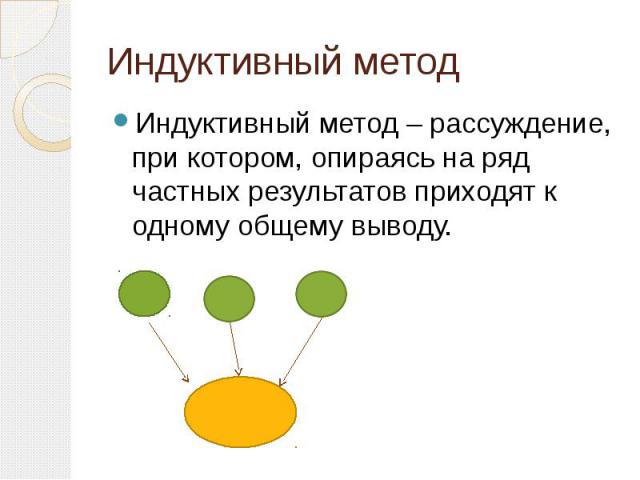
Индуктивный метод Индуктивный метод – рассуждение, при котором, опираясь на ряд частных результатов приходят к одному общему выводу.

Пример рассуждения по индукции Требуется установить, что каждое четное число в пределах от 4 до 100 можно представить в виде суммы двух простых чисел. Для этого переберем все интересующие нас числа и выпишем соответствующие суммы:

4=2+2; 6=3+3; 8=3+5; 10=5+5; ...; 4=2+2; 6=3+3; 8=3+5; 10=5+5; ...; 92=3+89; 94=5+89; 96=7+89; 98=9+89; 100=3+97. Эти 49 равенств (мы выписали только 9 из них) показывают, что утверждение о том, что любое четное число от 4 до100 можно представить в виде суммы двух простых чисел, верно и было доказано путем перебора всех частных случаев.

Это был пример полной индукции, когда общее утверждение доказывается для конечного множества элементов при рассмотрении каждого из этих элементов. Это был пример полной индукции, когда общее утверждение доказывается для конечного множества элементов при рассмотрении каждого из этих элементов. Но чаще общее утверждение относится не к конечному, а к бесконечному множеству. В таких случаях общее утверждение может быть угаданным, полученным неполной индукцией. Оно может оказаться верным или неверным.

Пример 1 Выдвинем гипотезу, что сумма первых n нечетных чисел равна n2. Рассмотрим на примерах: 1=12 ; 1+3=4=22 ; …; 1+3+5+7+9+11=36=62 Гипотеза подтвердилась, однако она останется гипотезой, пока не будет доказана. Доказательство: 1+2+5+…+(2n-1) – сумма n членов арифметической прогрессии, значит, Sn=

Пример 2 Рассмотрим последовательность Выпишем первые четыре члена: 19; y2 =23; y3 = 29; y4 = 37. Возникает гипотеза, что вся последовательность состоит из простых чисел. Однако это не так: У16 =162 +16 +17=16(16+1)+17= 17(16+1)= 17×17. Это составное число.

Итак, неполная индукция не считается в математике методом строгого доказательства, т.к. может привести к ошибке. Во многих случаях, когда доказательство найти трудно, обращаются к особому методу рассуждений, который называется методом математической индукции. Итак, неполная индукция не считается в математике методом строгого доказательства, т.к. может привести к ошибке. Во многих случаях, когда доказательство найти трудно, обращаются к особому методу рассуждений, который называется методом математической индукции.

Метод математической индукции Суть метода можно разъяснить на примере. Рассмотрим арифметическую прогрессию а1 , а2 , а3 , … аn , … . По определению значит, ;

Нетрудно догадаться, что для любого номера n справедливо равенство Нетрудно догадаться, что для любого номера n справедливо равенство Утверждение выведено нами интуитивно, попробуем обосновать его. Если n=1, то а1= а1 + (1-1)d – верное равенство, то есть утверждение для n=1 верно. Предположим, что утверждение верно для натурального числа n=k, т.е. предположим, что ak= а1+(k-1)d. И попробуем доказать, что утверждение верно для n=k+1, т.е. ak+1=а1+kd В самом деле по определению арифметической прогрессии ak+1=ak+d= (а1+(k-1)d)+d= а1+kd

Для n=1 утверждение Для n=1 утверждение верно. Мы оказали, что если для n=k эта формула верна, то и для n=k+1 формула тоже верна. Но т.к. формула верна для n=1, то она верна и для n=2, а значит и для n=3 и т.д. т.е формула верна для любого натурального числа n. Утверждение доказано.

Составляющие метода математической индукции Пусть нужно доказать справедливость А(n), где n – любое натуральное число. Для этого сначала проверим справедливость А(n) для n=1(базис математической индукции). Затем докажем, что для любого натурального числа k справедливо следующее: если А(k) – справедливо, то А(k+1), тоже справедливо(индукционный шаг). Делаем вывод, что А(n) справедливо для любого n.

Принцип математической индукции: Утверждение, зависящее от натурального числа n, справедливо для любого n, если выполнены следующие условия: А)утверждение верно для n=1; Б)из справедливости утверждения для n=k, где k – любое натуральное число, вытекает справедливость утверждения и для следующего натурального числа n=k+1