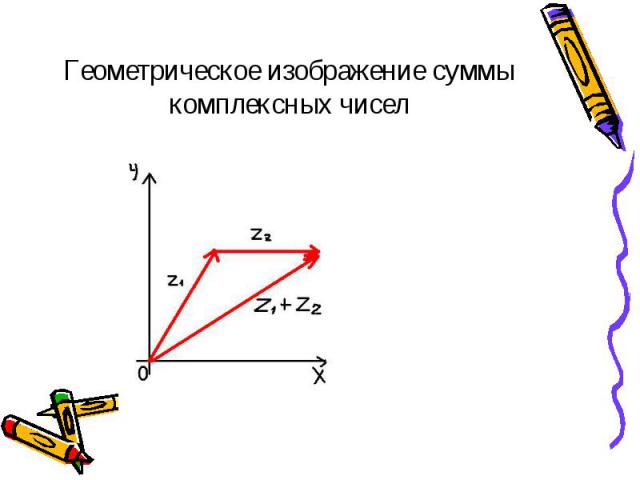
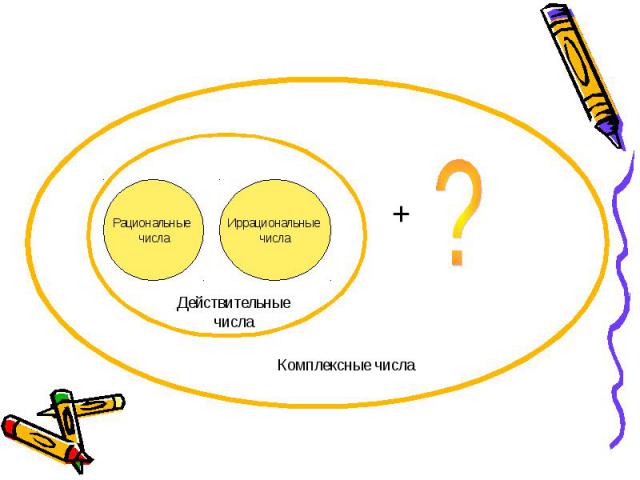
Презентация на тему: Комплексные числа


ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры.

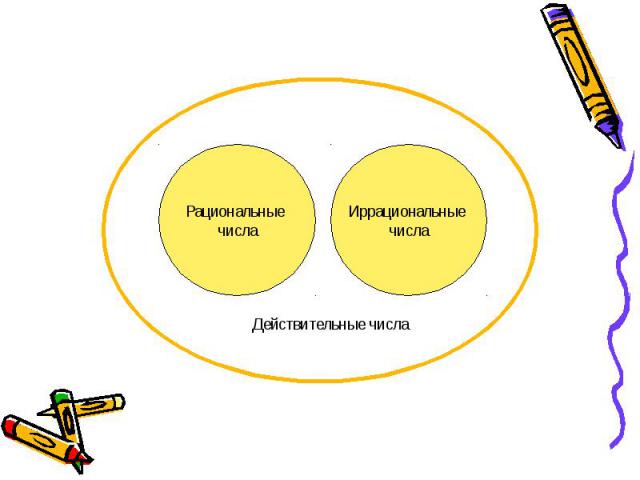
Х+А=В - недостаточно положительных Х+А=В - недостаточно положительных чисел А·Х + В=0 (А≠0) – разрешимы на множестве рац.чисел Х²=2 или Х³=5 - корни - иррациональные числа
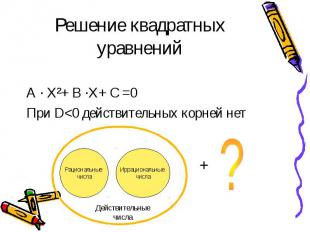
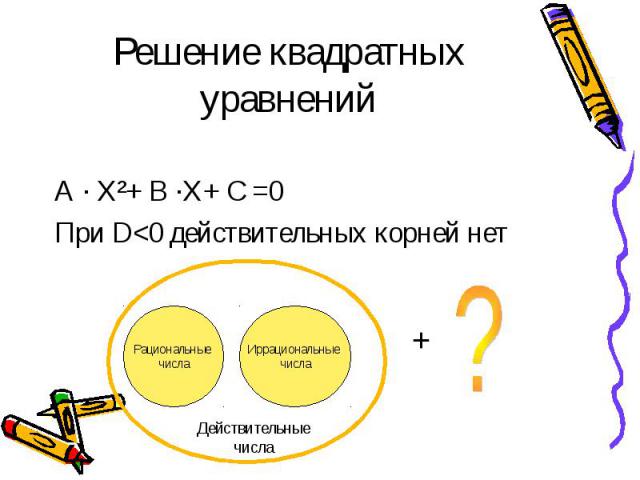
А · Х²+ В ·Х+ С =0 При D<0 действительных корней нет

Х²=-1 Х²=-1 Х=i -корень уравнения i- комплексное число, такое , что i²=-1

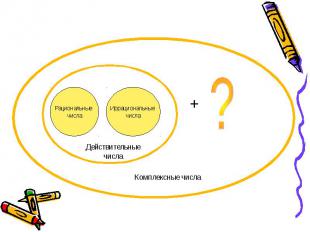
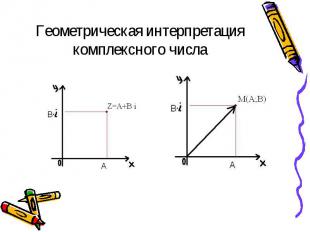
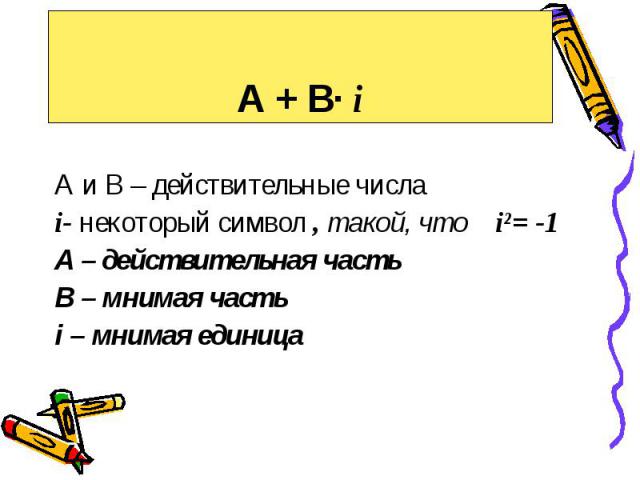
А и В – действительные числа i- некоторый символ , такой, что i²= -1 А – действительная часть В – мнимая часть i – мнимая единица

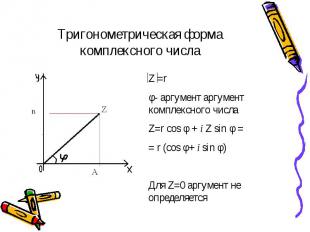
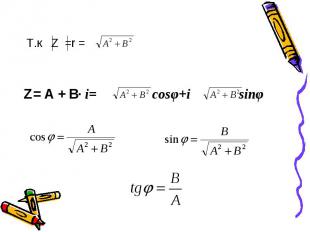
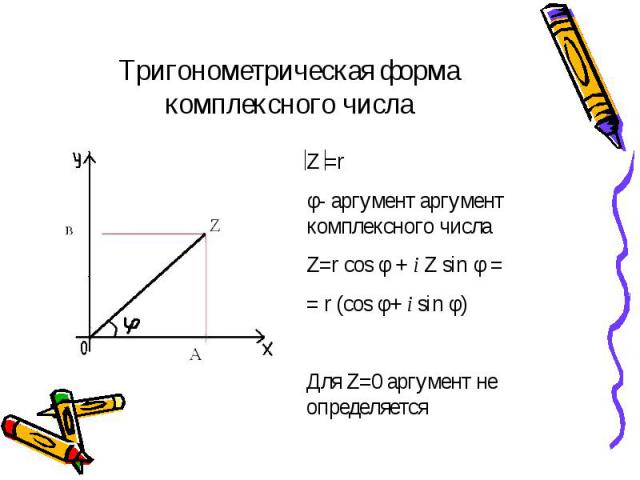
Т.к Z =r = Т.к Z =r =

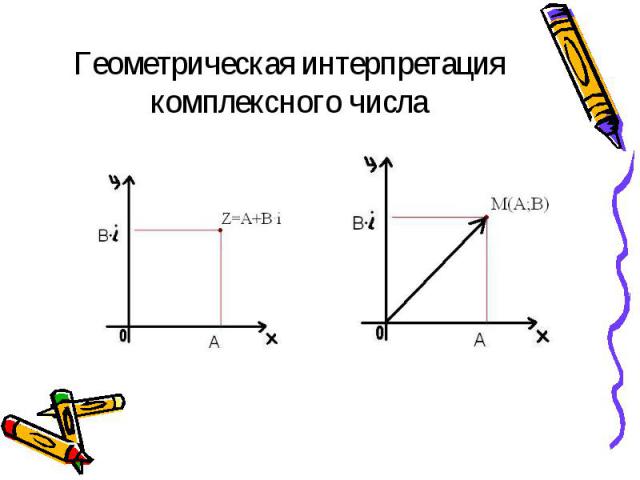
Алгебраическая форма Алгебраическая форма
![Если Z 1= Z2, то получим Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² ( Если Z 1= Z2, то получим Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² (](https://fs1.ppt4web.ru/images/95390/137189/310/img13.jpg)
Если Z 1= Z2, то получим Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² (cos2 φ+ i sin 2φ) Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+ i sin φ)= r³ (cos3 φ+ i sin 3φ)

Число Z называется корнем степени n из числа ω (обозначается ), если (*) Число Z называется корнем степени n из числа ω (обозначается ), если (*) Из данного определения вытекает, что каждое решение уравнения является корнем степени n из числа ω.


Решить уравнение: Решить уравнение:

Переместительное свойство: Переместительное свойство: Сочетательное свойство: Распределительные свойство:
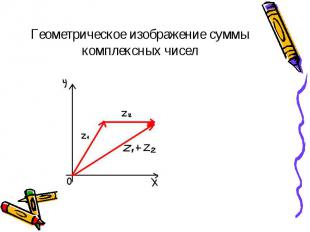

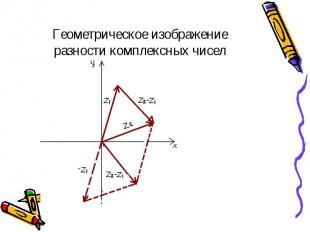

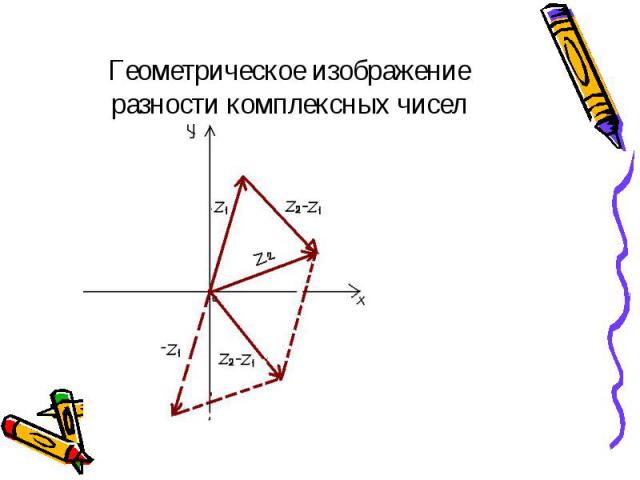
Найти разность и частное комплексных чисел Найти разность и частное комплексных чисел

Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др/ Алгебра и начала анализа 10-11кл, Просвещение 2005г, Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. и др/ Алгебра и начала анализа 10-11кл, Просвещение 2005г, Колмагоров А.Н., Абрамов, Дудицин/ Алгебра и начала анализа 10-11кл, Просвещение 2005г НикольскийС.М., Потапов Н.К, и др. Алгебра и начала анализа 10-11кл, Просвещение 2005г






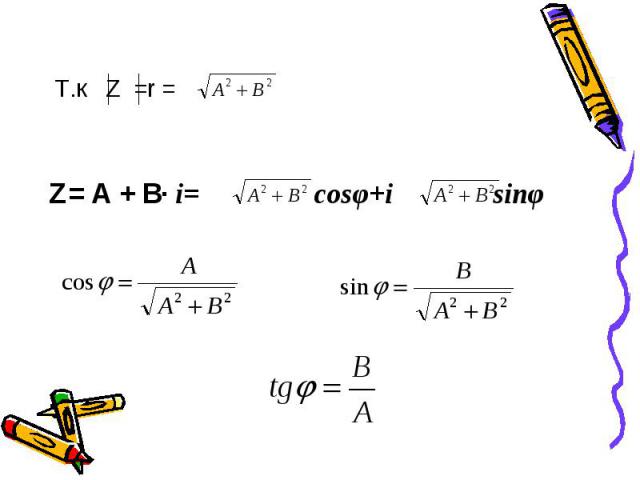

![Если Z 1= Z2, то получим Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² (cos2 φ+ i sin 2φ) Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+ i sin φ)= r³ (cos3 φ+ i sin 3φ) Если Z 1= Z2, то получим Если Z 1= Z2, то получим Z²=[r (cos φ+ i sin φ)]²= r² (cos2 φ+ i sin 2φ) Z³= Z²·Z=[r (cos φ+ i sin φ)]²·r (cos φ+ i sin φ)= r³ (cos3 φ+ i sin 3φ)](https://fs1.ppt4web.ru/images/95390/137189/640/img13.jpg)