Презентация на тему: комплексные числа

Комплексные числа

Поле комплексных чисел Поле действительных чисел (R) не является алгебраически замкнутым полем(т.е. многочлены с действительными коэффициентами могут не иметь действительных корней). Пример: Х2+1=0

Наша цель – построение расширения поля С, в котором есть такой элемент i, что i2=-1 Построение поля С окажется алгебраически замкнутым(алгебраическим замыканием поля С)

Для С характерно: Для a, b, c, d равенство a+bi=c+di выполняется тогда и только тогда, когда a=c, b=d (a+bi)+(c+di)=(a+c)+(b+d)i (a+bi)(c+di)=(ac-bd)+(ad+bc)i (a+bi)/(с+di)=(a+bi)(c-di)/(c2+d2)

Геометрическая интерпретация

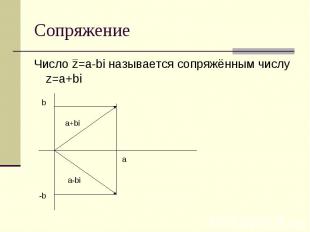
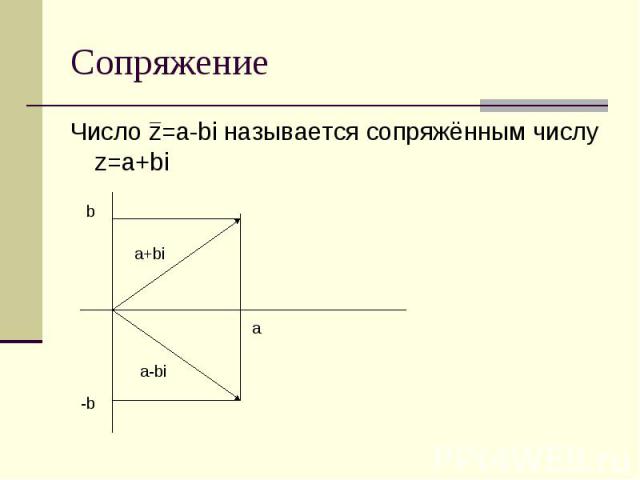
Сопряжение Число z=a-bi называется сопряжённым числу z=a+bi

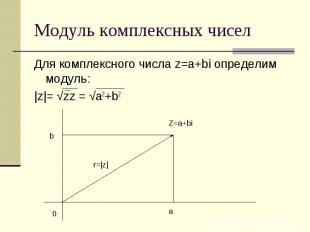
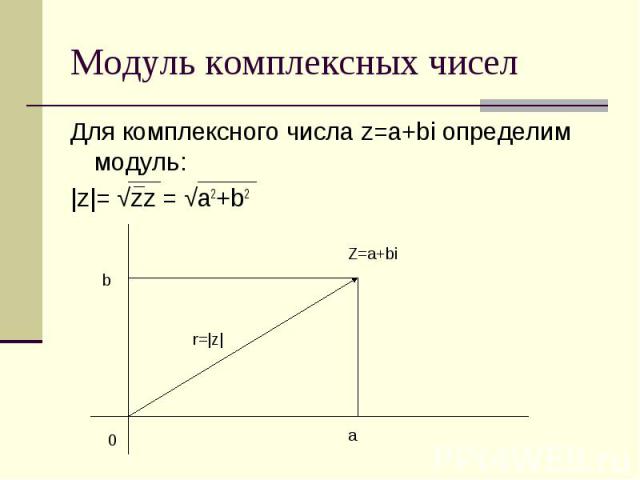
Модуль комплексных чисел Для комплексного числа z=a+bi определим модуль: |z|= √zz = √a2+b2

Тригонометрическая форма z=a+bi=r(cosφ+isinφ), r=√a2+b2 cosφ=a/√a2+b2 sinφ=b/√a2+b2

Умножение чисел в тригонометрической форме Для чисел: z1=r1(cosφ1+isinφ1), z2=r2(cosφ2+isinφ2) верно: z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)) Следствие: z1/z2=r1/r2(cos(φ1-φ2)+isin(φ1-φ2))

Формула Муавра (r(cosφ+isinφ))n=rn(cos(nφ)+isin(nφ))

Извлечение корня n-ой степени wk=n√r (cos(φ+2πk)/n+isin(φ+2πk)/n)

Теорема о разложении многочлена с комплексными коэффициентами в произведении линейных множителей Пусть f(x) из C, deg f(x)=n≥1 Тогда: f(x)=a(x-α1)…(x-αn), a,α1,…,αn из С