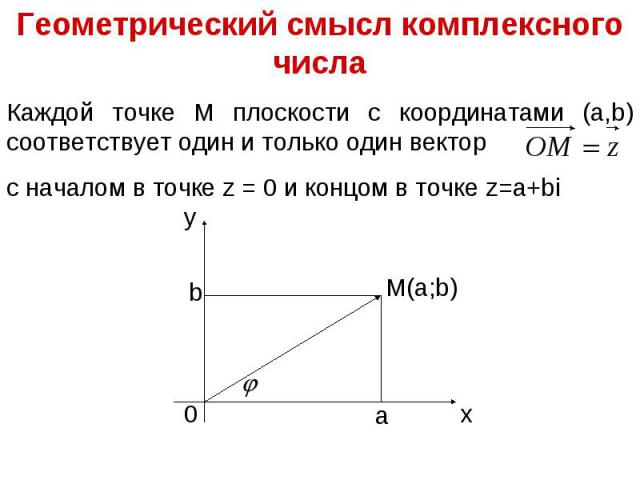
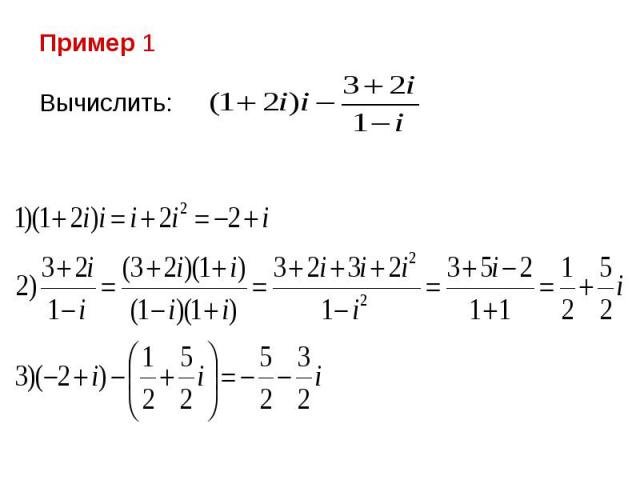Презентация на тему: Комплексные числа

Произведением комплексных чисел z = (a; b) и Произведением комплексных чисел z = (a; b) и w = (c; d) называют комплексное число (ac – bd; ad + bc) Частным от деления z на w называют число u, равное:

Если показатель степени i делится на 4, то значение степени равно 1, если при делении показателя на 4 в остатке получается 1, то значение степени равно i, если при делении показателя на 4 остаток равен 2, то значение степени равно -1, если в остатке при делении показателя на 4 будет 3, то значение степени равно –i. Если показатель степени i делится на 4, то значение степени равно 1, если при делении показателя на 4 в остатке получается 1, то значение степени равно i, если при делении показателя на 4 остаток равен 2, то значение степени равно -1, если в остатке при делении показателя на 4 будет 3, то значение степени равно –i.

Вычислить: 1) i 66 , 2) i143 , 3) i216 ,4)i137 Вычислить: 1) i 66 , 2) i143 , 3) i216 ,4)i137 Решение: 1) i66 66:4=16(2). Остаток равен 2, значит i66=-1 2)i143 143 :4=35(3).В остатке 3, значит i 143=-i 3)i216 216:4=54(0).в остатке 0, значит i216=1 4)i137 137:4=34(1).В остатке 1, значит i137=i

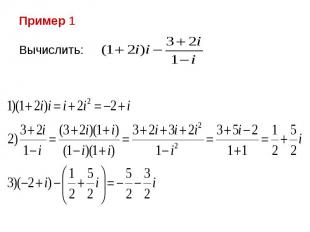
Пример2. Пример2. Записать в тригонометрической форме: Сначала находим модуль числа: Далее, согласно формулам (*), имеем: Учитывая, что угол

При возведении комплексного числа При возведении комплексного числа z = r (Cosφ + iSinφ) в натуральную степень n модуль данного числа возводится в эту степень, а аргумент умножается на показатель степени: формула Муавра

Корень n-й степени из комплексного числа z = r (Cosφ + iSinφ) имеет n различных значений, которые находятся по формуле :

Пример: Записать число в показательной форме. Пример: Записать число в показательной форме.

Действия над комплексными числами, заданными в показательной форме Действия над комплексными числами, заданными в показательной форме

Для вычисления корня из комплексного числа Для вычисления корня из комплексного числа

Пусть D – некоторая область на комплексной плоскости Пусть D – некоторая область на комплексной плоскости

- n-значная функция; - n-значная функция; -бесконечнозначная функция. Если функция однозначна,то она может быть задана в виде отображения В таком случае функция называется однолистной .В дальнейшем, если не указано особо,будем рассматривать однолистные функции.

Пример: Для функции найти Пример: Для функции найти Решение: Подставим в место z значение i в функцию Ответ: f(i)=1

Пусть дана функция , Представим z в алгебраической форме Значение f(x)-комплексное число,т.е. ,которое также можем представить в алгебраической форме ,где и -действительные функции комплексного аргумента,но задание я эквивалентно заданию пары(x,y).Окончательно,любую функцию комплексного аргумента можно представить в виде Пусть дана функция , Представим z в алгебраической форме Значение f(x)-комплексное число,т.е. ,которое также можем представить в алгебраической форме ,где и -действительные функции комплексного аргумента,но задание я эквивалентно заданию пары(x,y).Окончательно,любую функцию комплексного аргумента можно представить в виде ,где и -действительные функции двух действительных переменных.Функции u и v называются компонентами функции f(z),u- действительная компонента,v-мнимая компонента.Пишут :

Пример: Для функции Пример: Для функции Где найти ее действительную и мнимую часть. Решение: (x+iy)2+4i=x2+2ixy-y2+4i=(x2-y2)+(2xyi+4i)=(x2-y2)+i(2xy+4). Тогда действительная часть функции f(z) - x2-y2,а мнимая - 2xy+4.

Понятие непрерывности определяется аналогично действительному случаю. Понятие непрерывности определяется аналогично действительному случаю. F(z)-непрерывна в точке Так как это определение формально совпадает с обычным ,то все свойства непрерывной функции комплексного аргумента совпадают дословно со свойствами действительных функций.