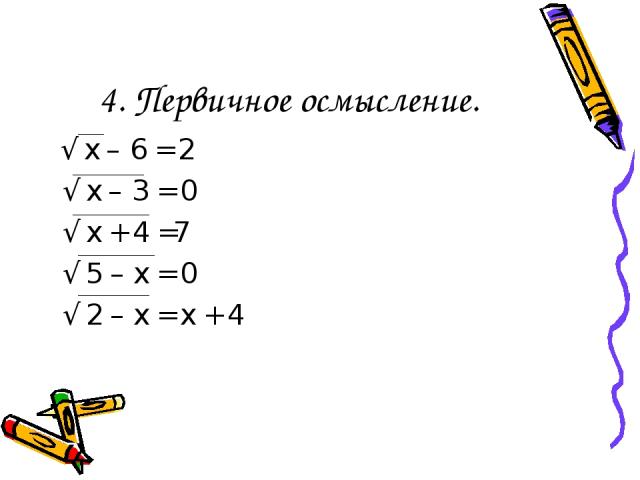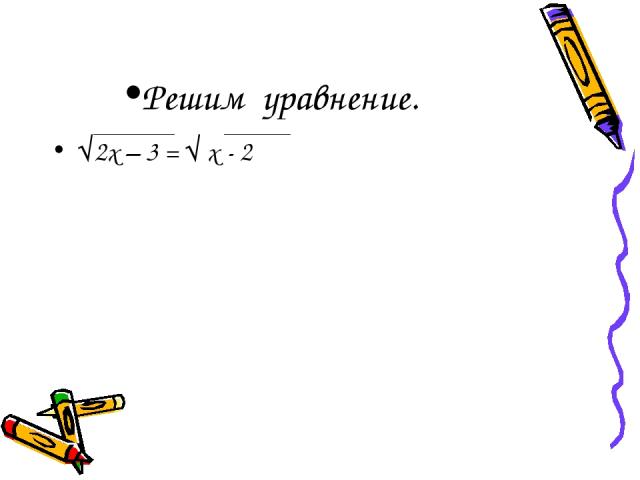Презентация на тему: Иррациональное уравнение

Иррациональные уравнения «Урок-дискуссия» 900igr.net

Введение ПРОБЛЕМА: Учащиеся не всегда умеют сознательно использовать информацию об иррациональных уравнениях. Грамотно применять свойства корней степени выше третьей, а так же степени с дробным показателем. ЦЕЛИ: 1. Ввести понятие иррациональных уравнений и показать способы их решений. 2. Развивать умение выделять главное, существенное в изучаемом материале, обобщать факты и понятия, развивать самостоятельность, мышление, познавательный интерес. 3. Содействовать формированию мировоззренческих понятий. ОБЪЕКТ ИССЛЕДОВАНИЯ: Организация применения различных способов решения иррациональных уравнений, уравнений с параметром.

Ход урока Организация урока. (1мин.) Постановка целей, принятие их учащимися.(2 мин.) Вопрос, раскрывающий сущность проблемы. Дискуссия о возможных путях её решений.(3 мин.) Ознакомление с новым материалом. (20 мин.) Первичное осмысление и применение изученного. ( 7 мин.) Закрепление изученного материала.(10 мин.) Постановка домашнего задания. ( 1 мин.) Подведение итогов урока (2 мин.) Резервные задания.

Начало урока Здравствуйте! Надеюсь ,что у вас серьезный настрой на урок. Желаю вам высоких результатов. В ходе дискуссии нам необходимо поразмышлять и сформулировать свои мысли, чтобы найти ответ на поставленный вопрос. В споре недопустимы оскорбления, упреки, недоброжелательность в отношении к своим одноклассникам.

2.Вопрос - проблема Какой шаг в решении уравнения приводит к появлению лишних корней.

Найди ошибку. 16 -36 =25 – 45 16-36+20,25=25-45+20,25 (4-4,5)² =(5-4,5)² 4-4,5=5-4,5 4=5 Вывод: Если квадраты двух выражений равны, то их основания либо равны между собой, либо противоположны.

3. Изучение нового материала. Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Устно: какие из следующих уравнений являются иррациональными? а) х + √ х = 2 д) х + √ х = 0 б) х √7 = 11+х е) у² - 3 √ 2 = 4 в)у + √ у²+9 = 2 г)√ х – 1 = 3 Какое уравнение не имеет корней?

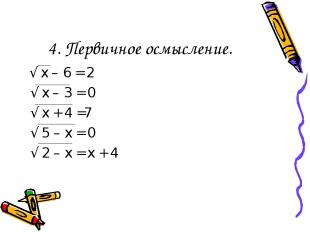
4. Первичное осмысление. √ х – 6 = 2 √ х – 3 = 0 √ х + 4 =7 √ 5 – х = 0 √ 2 – х = х + 4

Алгоритм решения уравнений. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение. Иногда удобнее решать иррациональные уравнения, область допустимых значений неизвестного и используя равносильные переходы. ⁿ√ƒ (x) = g ( х ) {ƒ ( x ) = gⁿ (x) g ( х ) ≥ o

5. Закрепление изученного материала. Является ли число x корнем уравнения: а) √ х – 2 = √2 – х , х0 = 4 б) √2 – х = √ х – 2, х0 = 2 в) √ х – 5 = √ 2х – 13, х0 = 6 г) √ 1 – х = √ 1 + х, х0 = 0.

Решим уравнение: √ х + 2 = х Решение: х + 2 = х2, х2 – х – 2 = 0 х1 = и х2 = Проверка: При х = 2, 2=2, верно. При х = -1, 1= -1, ложно Ответ: х = 2 2 -1

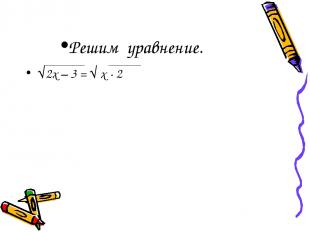
Решим уравнение. √2х – 3 = √ х - 2

Решение Возведем обе части уравнения в квадрат, получим: 2х -3 = х -2 , х = 1 Проверка: √2•1 – 3 = √ 1 – 2,обе части уравнения не имеют смысла. Ответ: корней нет

История неразумных чисел История иррациональных чисел относится к удивительному открытию пифагорийцев. А началось это с простого вопроса, связанного с вычислением диагонали квадрата, сторона которого равна 1. \ подробно расскажет Катя П.\ Выполняем самостоятельно: 899 (а, б ,в) 900 (а, б ,в) ( б ) проверяем по решению на доске.*

6. Задание на дом. № 900 ( г, д, е ) № 901 ( а, г ) Стр. 265 \ теория \

7. Подведение итогов урока. Ф. И. Учащегося. * домашнее задание Сам. Учитель. * устная работа * новая работа Ю.Н. Макарычев