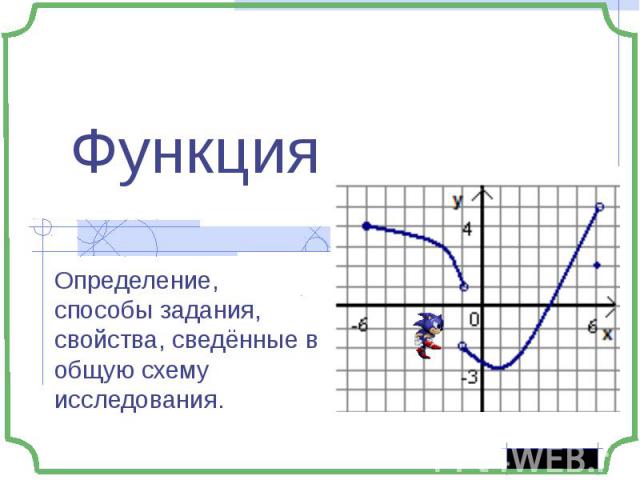
Презентация на тему: Функция

Обобщить теоретические знания по теме. Обобщить теоретические знания по теме. Рассмотреть решения задач, связанных с этой темой, базового и повышенного уровня. Организовать работу учащихся соответственно уровню уже сформированных у них знаний.

I этап – организационный (1 мин.) I этап – организационный (1 мин.) II этап – повторение теоретического материала по теме (20 мин.) III этап – разноуровневая самостоятельная работа (15 мин.) IV этап – подведение итогов урока, комментарии по домашнему заданию (4 мин.)

Тема урока: «Определение, способы задания, свойства, сведённые в общую схему исследования». Тема урока: «Определение, способы задания, свойства, сведённые в общую схему исследования». Цели урока: Обобщить теоретические знания по теме. Рассмотреть решения задач, связанных с этой темой, базового и повышенного уровня.

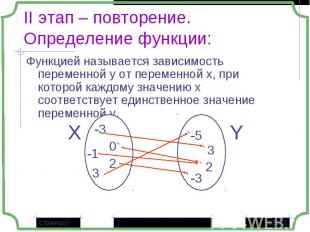
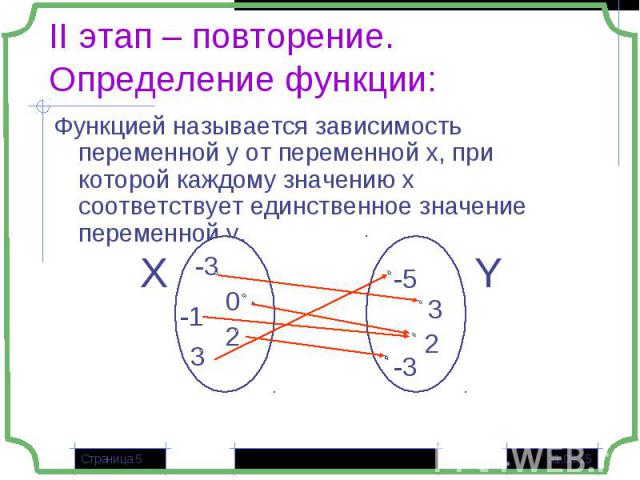
Функцией называется зависимость переменной у от переменной х, при которой каждому значению x соответствует единственное значение переменной y. Функцией называется зависимость переменной у от переменной х, при которой каждому значению x соответствует единственное значение переменной y.

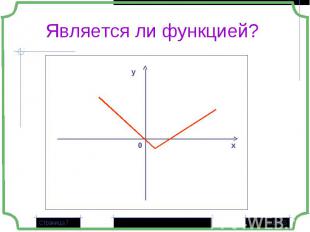
Описательный: «Каждому двузначному числу поставлен в соответствие его квадрат» Описательный: «Каждому двузначному числу поставлен в соответствие его квадрат» Табличный Графический Аналитический

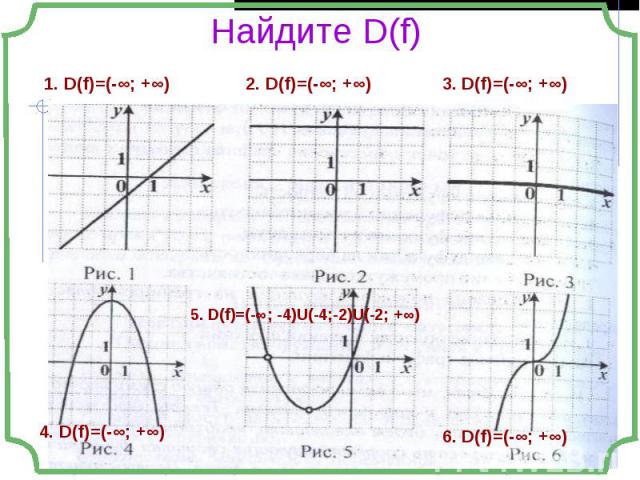
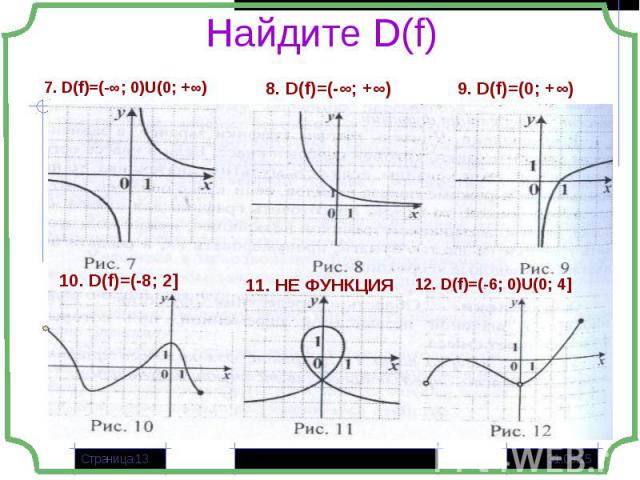
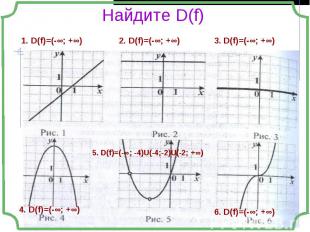
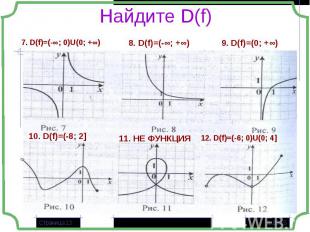
Область определения функции D(f) Область определения функции D(f) Точки пересечения графика с осями координат Чётность, нечётность Монотонность Экстремумы Периодичность Знакопостоянство Область значений E(f) Построение графика

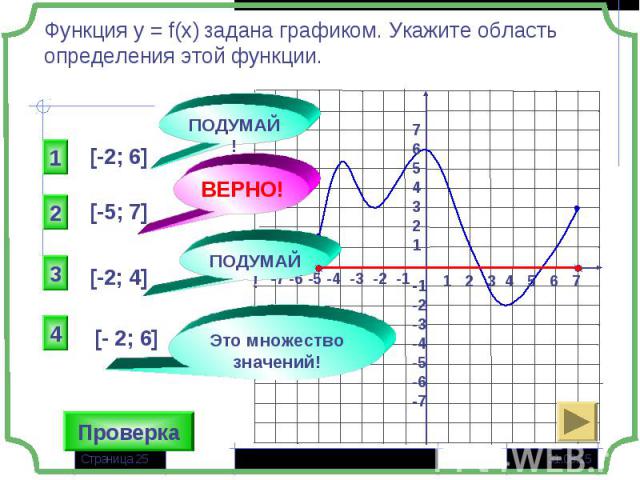
- Множество значений независимой переменной, при которых функция имеет смысл. - Множество значений независимой переменной, при которых функция имеет смысл. Функция – многочлен Функция задана в виде дроби Функция задана в виде корня чётной степени Функция содержит логарифмическое выражение Композиция функций

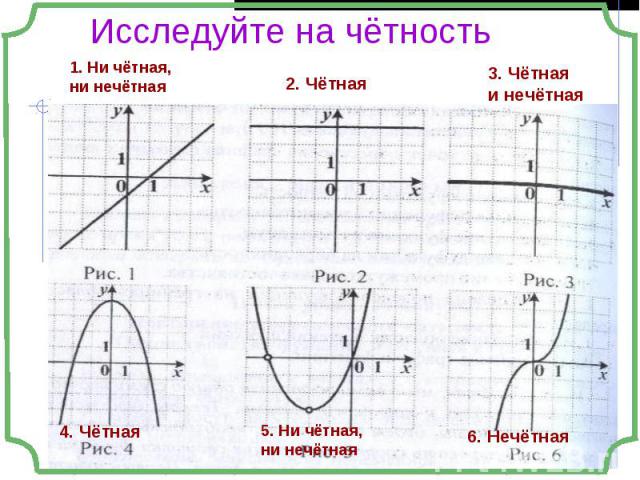
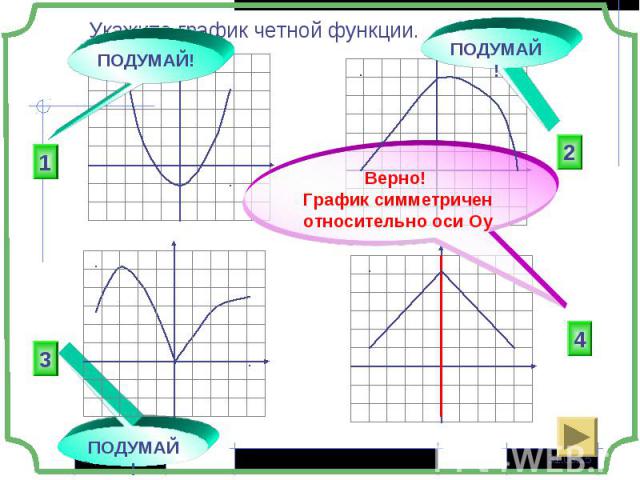
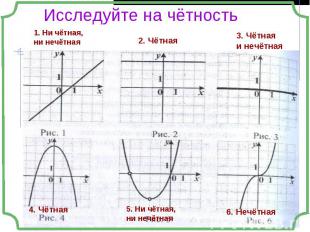
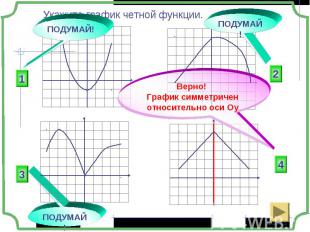
Если область определения функции симметрична относительно нуля Если область определения функции симметрична относительно нуля и для любого х из области определения выполняется равенство f(-x) = f(x), то функция чётная; и для любого х из области определения выполняется равенство f(-x) = - f(x), то функция нечётная;

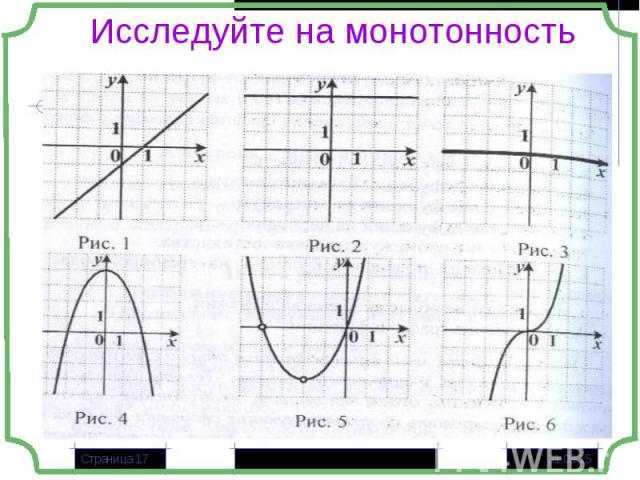
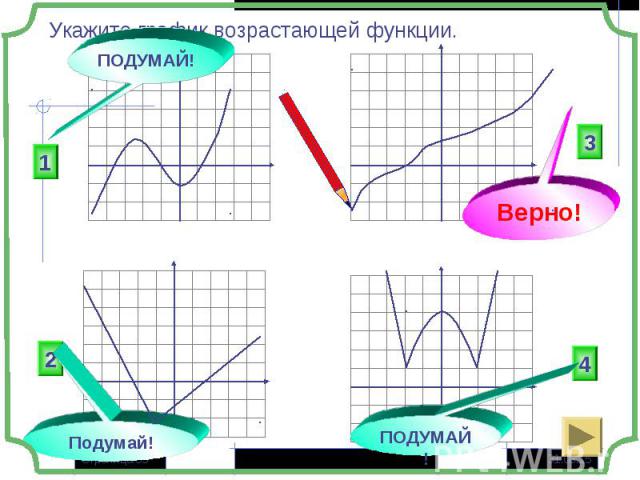
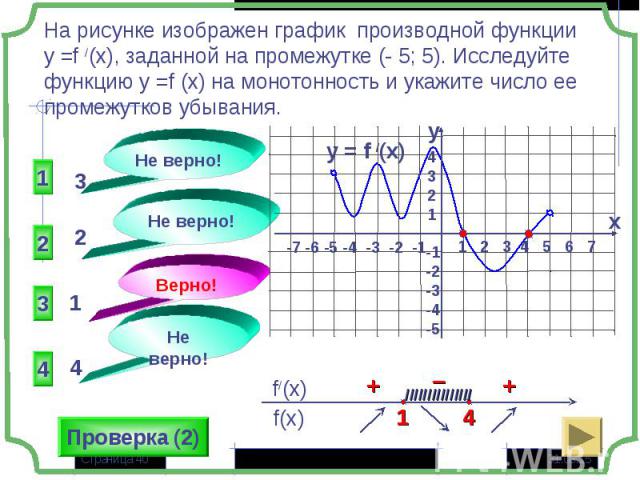
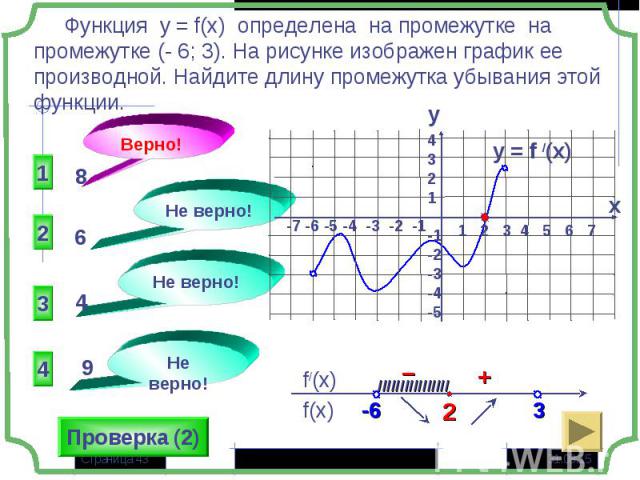
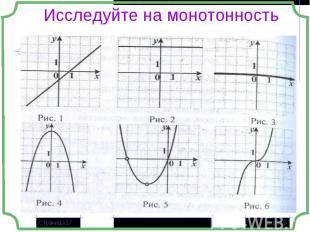
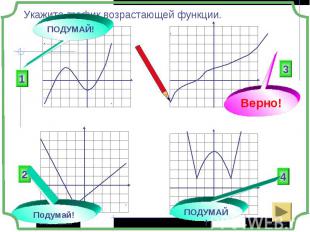
Если большему значению аргумента соответствует большее значение функции, то функция называется монотонно возрастающей x1> x2 и f(x1) > f(x2) Если большему значению аргумента соответствует большее значение функции, то функция называется монотонно возрастающей x1> x2 и f(x1) > f(x2) Если большему значению аргумента соответствует меньшее значение функции, то функция называется монотонно убывающей x1> x2 и f(x1) < f(x2)

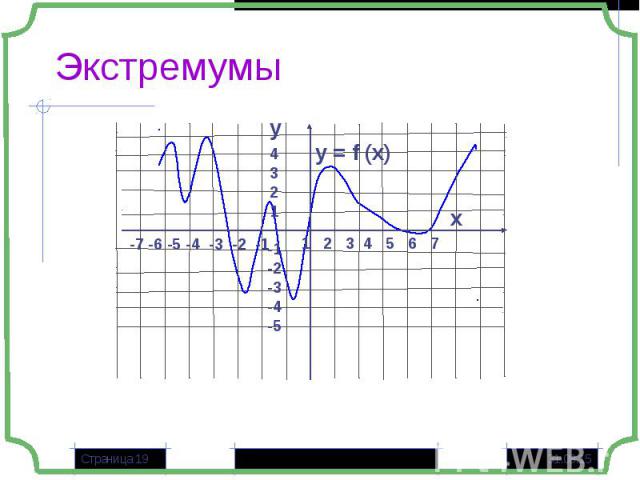
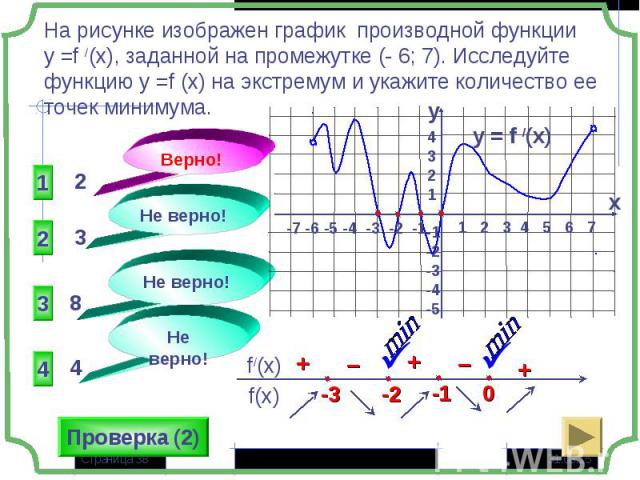
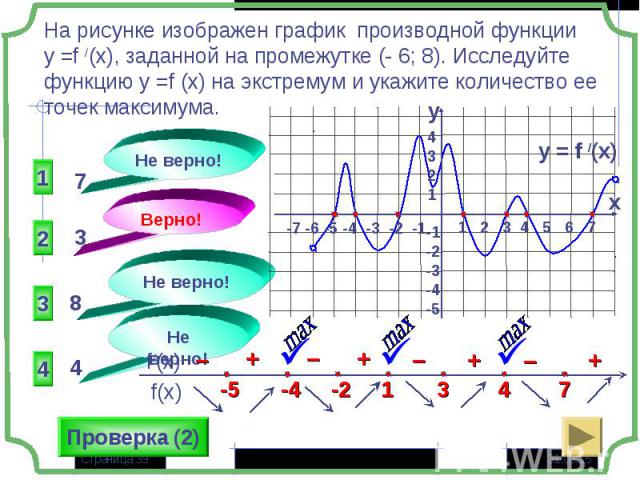
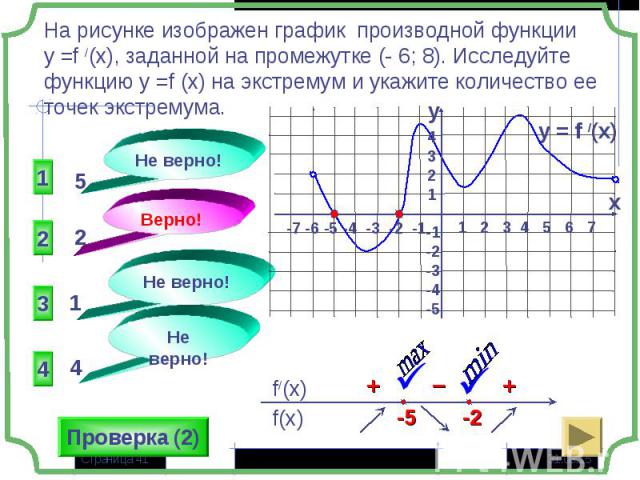
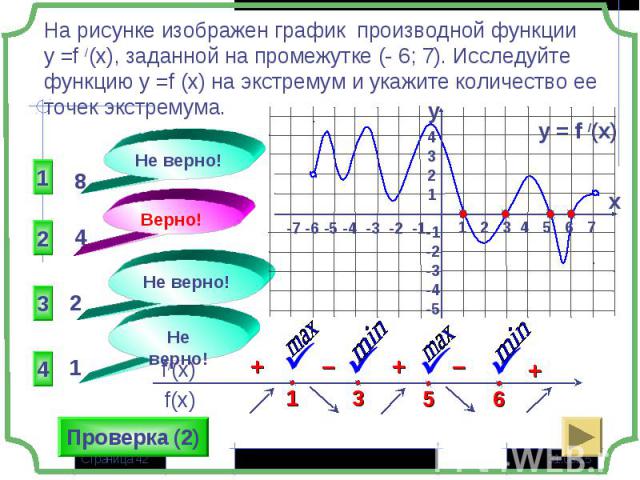
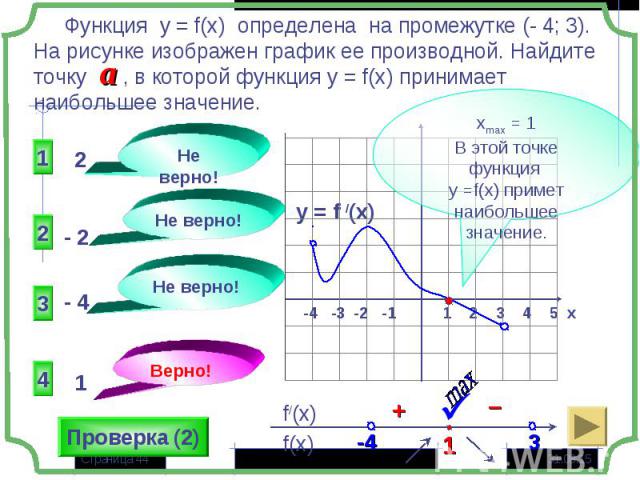
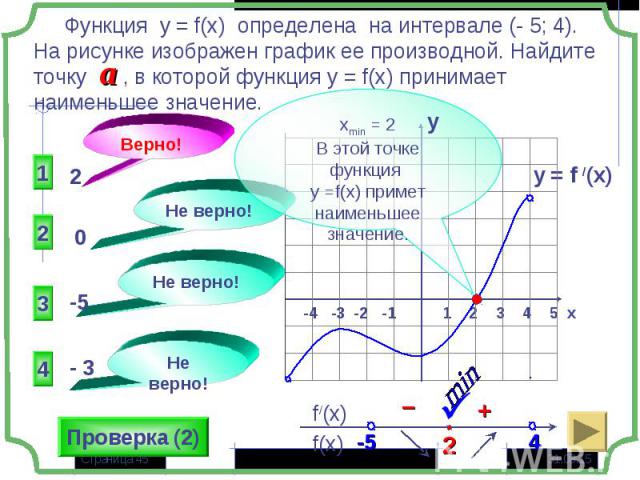
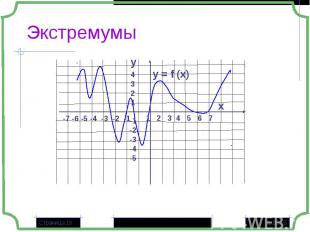
Если в некоторой точке х0 значение функции больше значений функции в окрестности этой точки, то х0- точка максимума (хmax= х0), а f(х0) – максимум функции (уmax= f(х0) – «гребни функции») Если в некоторой точке х0 значение функции больше значений функции в окрестности этой точки, то х0- точка максимума (хmax= х0), а f(х0) – максимум функции (уmax= f(х0) – «гребни функции») Если в некоторой точке х0 значение функции меньше значений функции в окрестности этой точки, то х0- точка минимума (хmin= х0), а f(х0) – минимум функции (у min = f(х0) – «впадины функции)

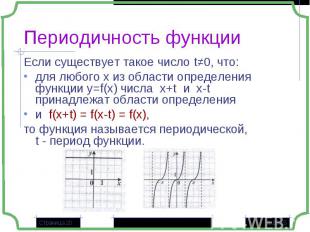
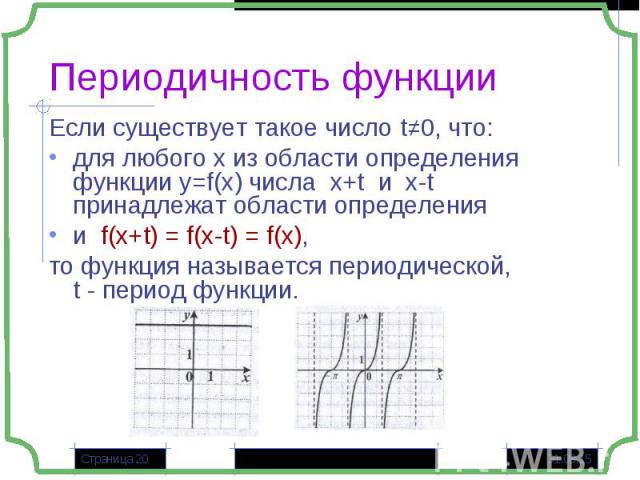
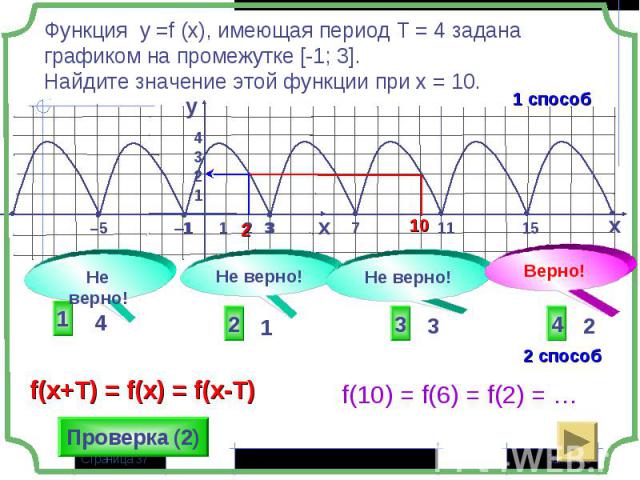
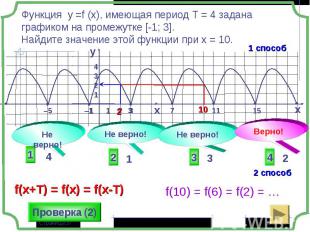
Если существует такое число t≠0, что: Если существует такое число t≠0, что: для любого х из области определения функции у=f(x) числа x+t и x-t принадлежат области определения и f(x+t) = f(x-t) = f(x), то функция называется периодической, t - период функции.

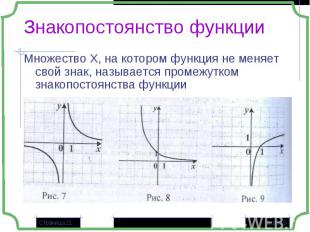
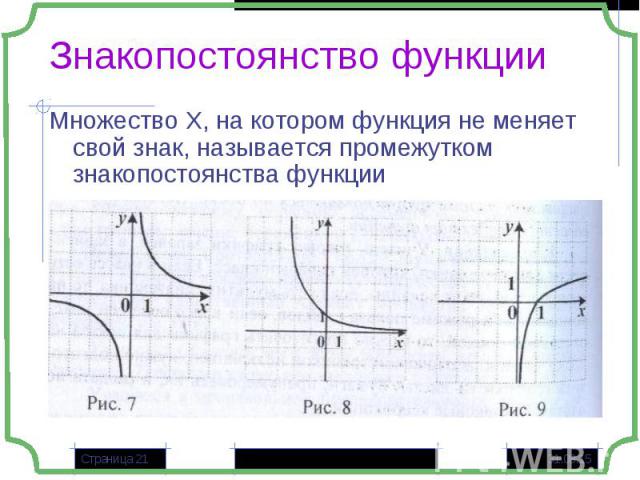
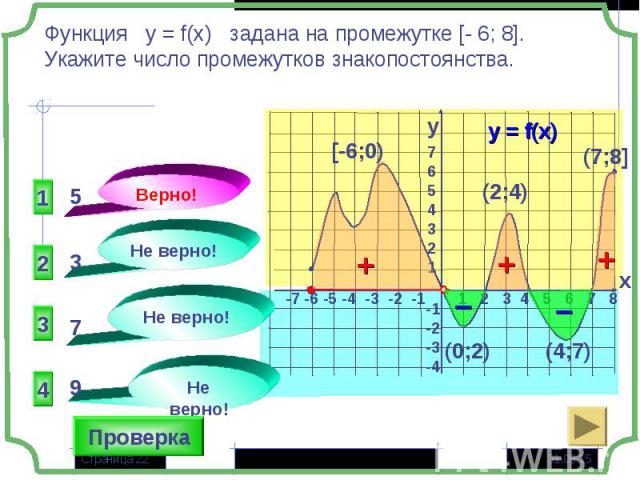
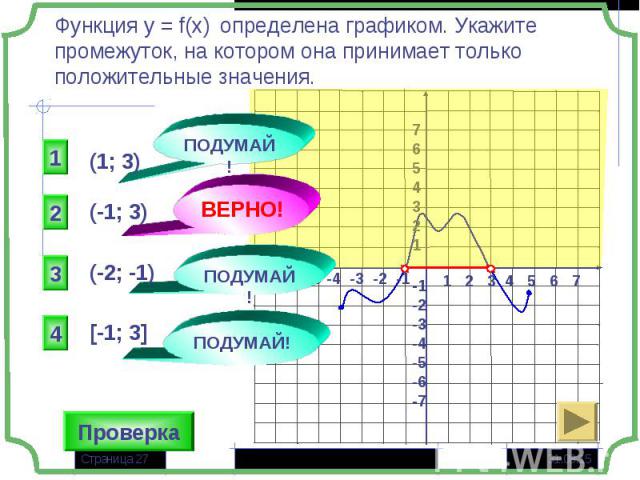
Множество Х, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции Множество Х, на котором функция не меняет свой знак, называется промежутком знакопостоянства функции

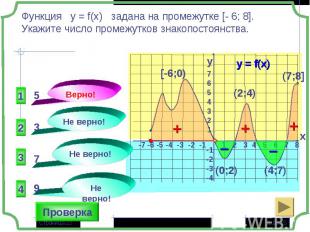
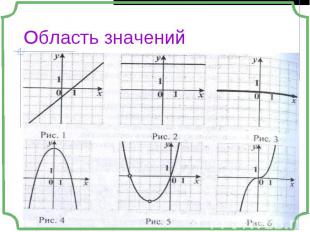
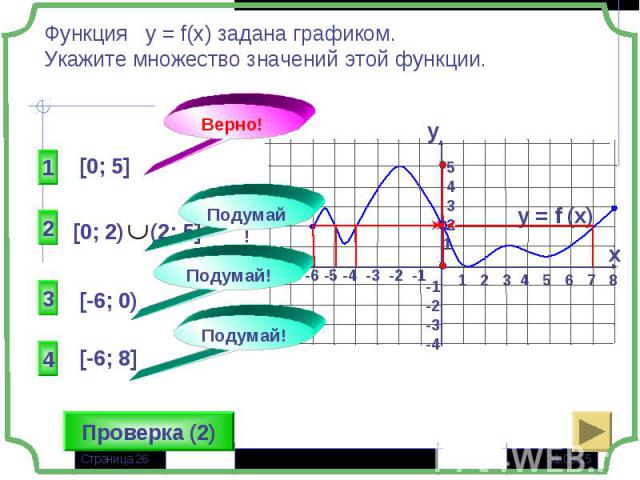
Множество, состоящее из всех значений, которые может принимать функция на своей области определения Множество, состоящее из всех значений, которые может принимать функция на своей области определения

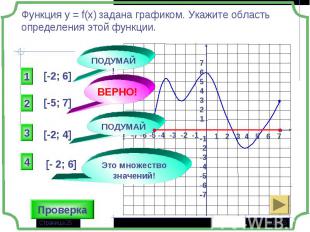
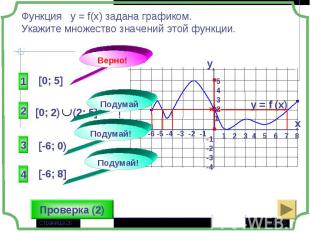
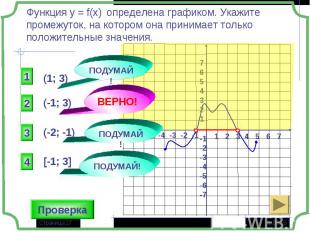
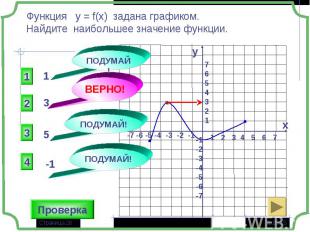
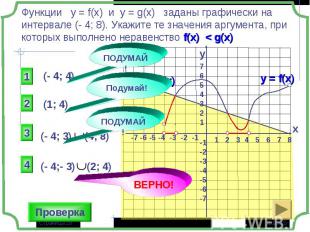
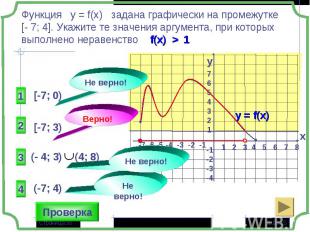
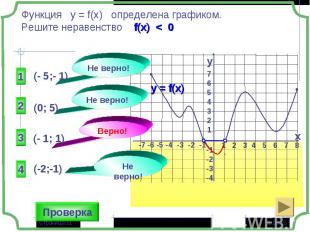
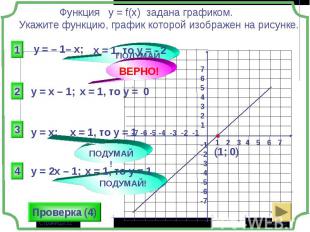
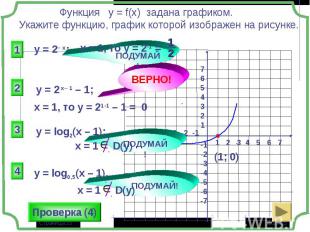
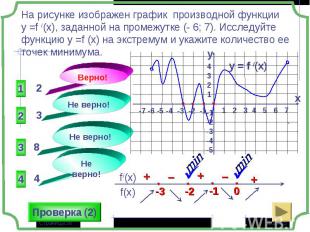
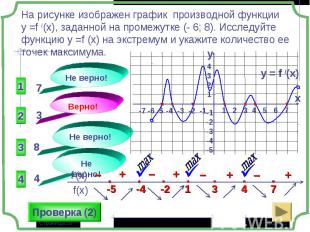
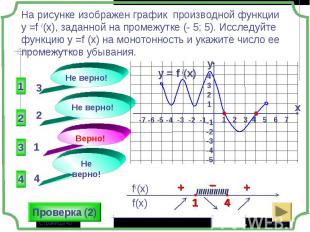
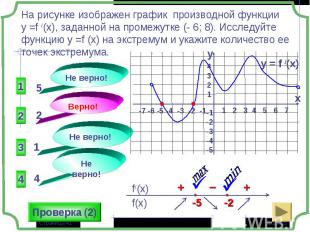
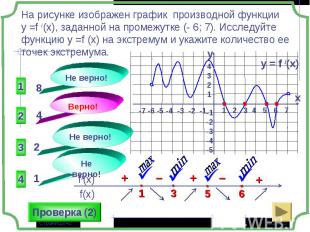
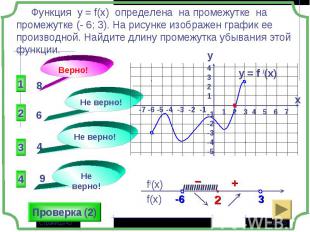
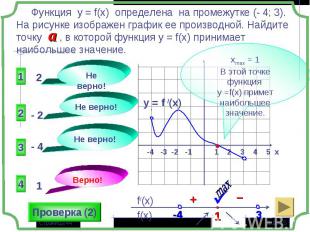
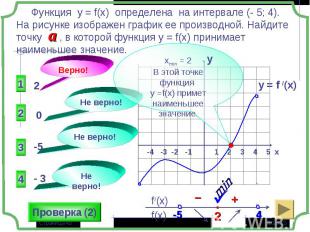
1 группа – карточки жёлтые. 1 группа – карточки жёлтые. 2 группа – карточки розовые. 3 группа – разбираем решение задания: Найдите все значения параметра а, при которых в области определения функции не содержится ни одного двузначного числа

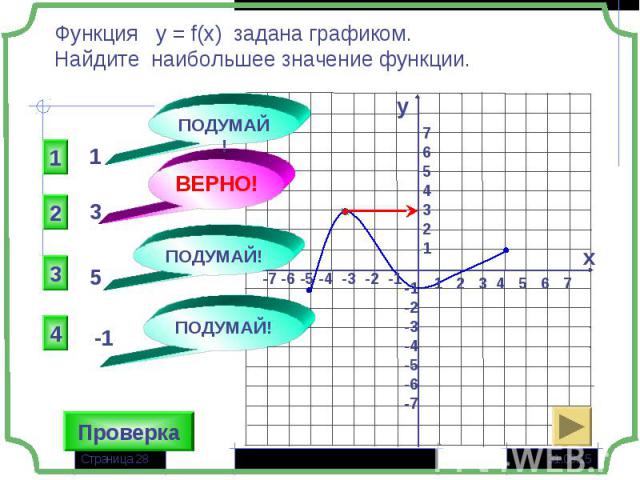
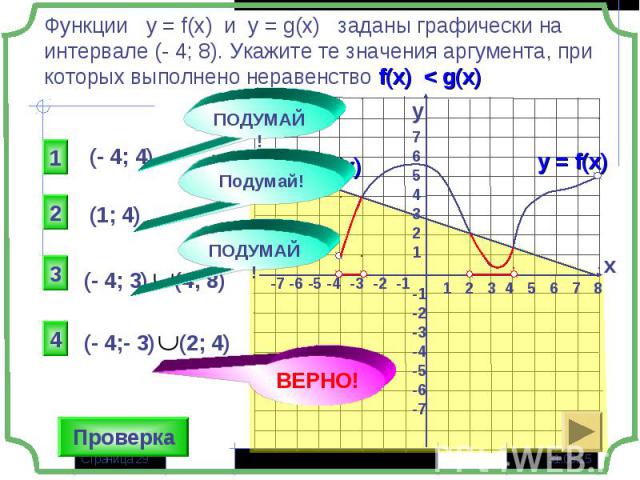
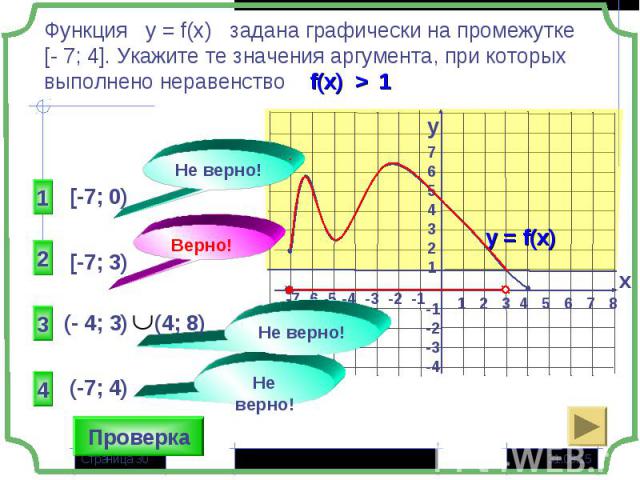
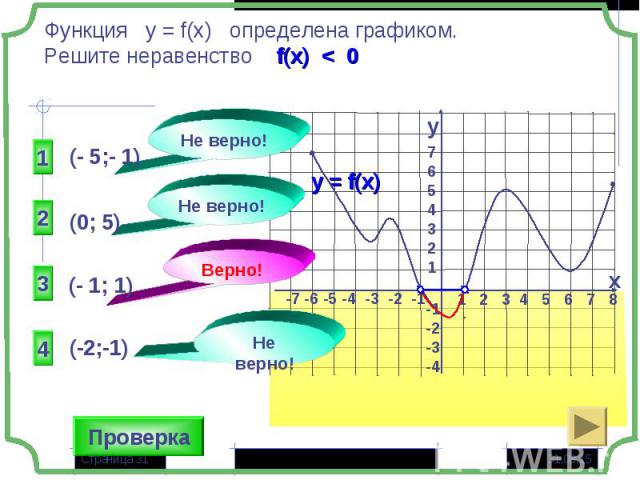
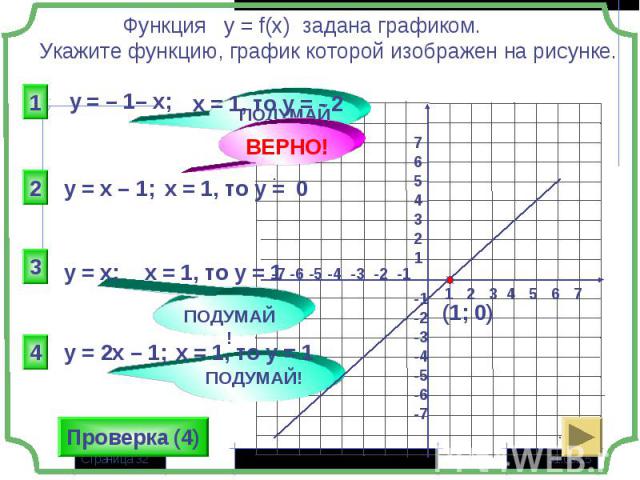
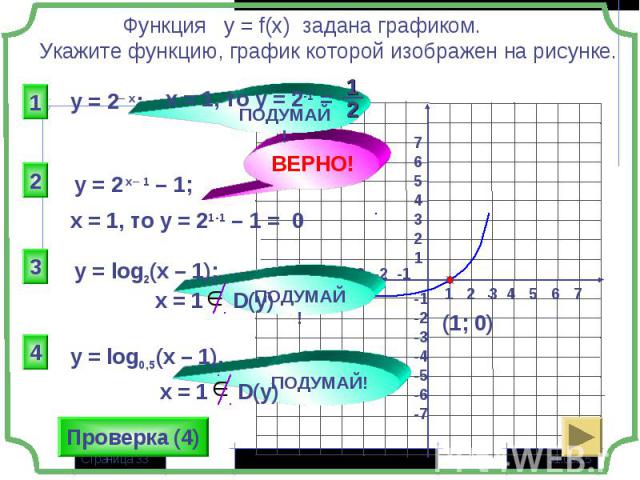
Тест по теме «Функция и её свойства» Тест по теме «Функция и её свойства»