Презентация на тему: «Функции» алгебра

11 класс экстернат 5klass.net

Производная Производной функции f в точке х0 называется число, к которому стремится разностное отношение при Δх, стремящемся к нулю.

Правила дифференцирования

Пример

Производная сложной функции

Пример

Производная тригонометрических функций

Пример

Метод интервалов

Пример

Возрастание (убывание) функции Найти промежутки возрастания и убывания функции:

Пример

Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции

Признак максимума функции Если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума

Признак минимума функции Если в точке х0 производная меняет знак с минуса на плюса, то х0 есть точка минимума

Пример Исследовать на экстремумы функцию

Решение х=2 (меняет знак с плюса на минус) – точка максимума х= 3 (меняет знак с минуса на плюс) – точка минимума

Исследование функций и построение их графиков

Схема исследования функции (10 класс) Найти область определения и значения данной функции Выяснить, обладает ли функция особенностями, облегчающими исследование, т.е. является ли функция: а) четной или нечетной; б) периодической Вычислить координаты точек пересечения графика с осями координат Найти промежутки знакопостоянства функции выяснить, на каких промежутках функция возрастает, а на каких убывает Найти точки экстремума, вид экстремума (max или min) и вычислить значения функции в этих точках Исследовать поведение функции в окрестности характерных точек, не входящих в область определения и при больших (по модулю) значениях аргумента

Исследовать функцию и построить ее график:

Решение Область определения: D (y) = R Четность, нечетность, периодичность тогда функция является ни четной ни нечетной ни периодическая

3. Найдем точки пересечения графика с Ох (у = 0):

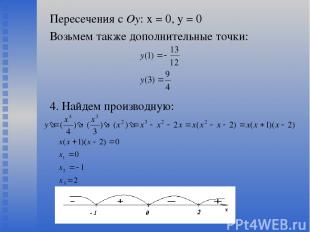
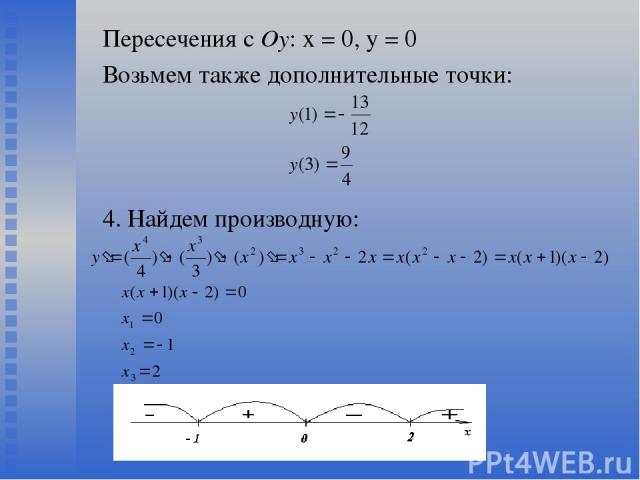
Пересечения с Оу: х = 0, у = 0 Возьмем также дополнительные точки: 4. Найдем производную:

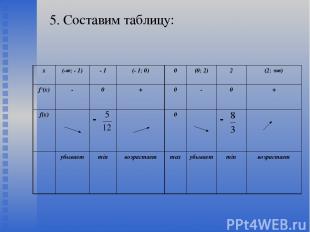
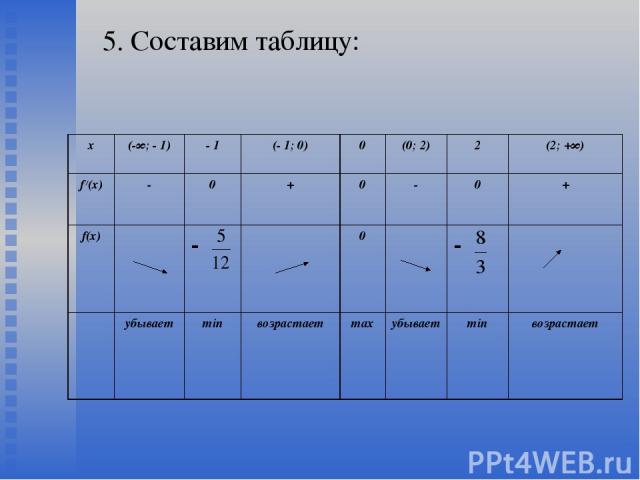
5. Составим таблицу: х (-∞; - 1) - 1 (- 1; 0) 0 (0; 2) 2 (2; +∞) f /(х) - 0 + 0 - 0 + f(х) - 0 - убывает min возрастает max убывает min возрастает

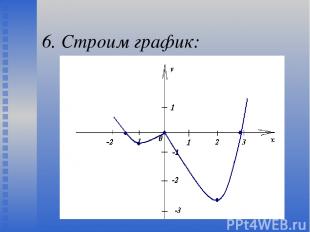
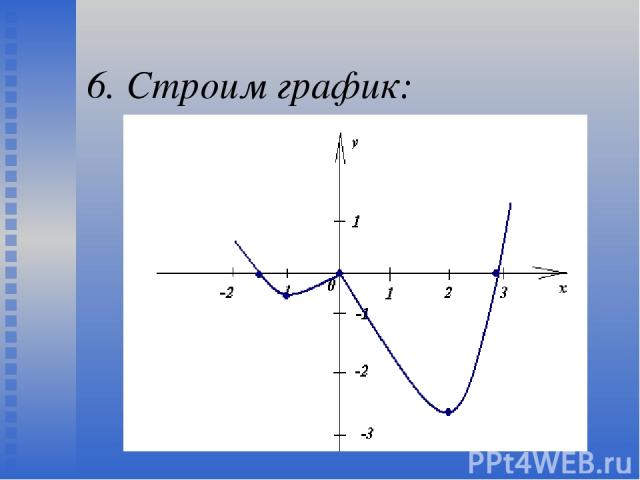
6. Строим график:

Наибольшее и наименьшее значение функции Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезках, а затем из полученных чисел выбрать наибольшее и наименьшее.

Пример Найдем наибольшее и наименьшее значения функции на отрезке

Определение первообразной. Основное свойство первообразной

Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка

Пример № 1 Функция есть первообразная для функции на интервале (- ∞;∞), т.к.

Пример № 2

Решить

Теорема Любая первообразная для функции f на промежутке I может быть записана в виде F(x) + C, где F(x) – одна из первообразных для функции f(x) на промежутке I, а С – произвольная постоянная

Таблица первообразных Функция k (постоянная) sinx cosx Общий вид первообразных для f kx + C -cosx+C sinx + C tgx+C -ctgx+C

Правило № 1 Если F есть первообразная для f, а G – первообразная для g, то F + G есть первообразная для f + g

Пример Найти общий вид первообразных для функции

Правило № 2 Если F есть первообразная для f, а k- постоянная, то функция kF – первообразная для kF

Пример Найдем одну из первообразных для функции

Правило № 3 Если F(х) есть первообразная для f(x), а k и b – постоянные, причем k ≠ 0, то есть первообразная для f(kx + b)

Пример Найдем одну из первообразных для функции

Решить

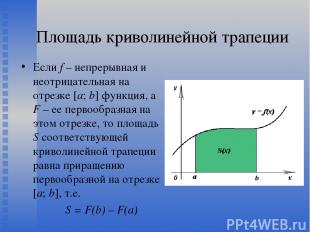
Площадь криволинейной трапеции Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b], т.е. S = F(b) – F(a)

Пример Вычислим площадь S криволинейной трапеции, ограниченной графиком функции , прямыми у = 0, х = 1 и х = 2

Понятие об интеграле Для любой непрерывной на отрезке [a; b] функции f (не обязательно неотрицательной) Sn при n → ∞ стремится к некоторому числу. Это число называется интегралом функции f от a до b и обозначается

Читается: «Интеграл от a до b эф от икс дэ икс» Числа a и b – пределы интегрирования: а – нижний предел, b – верхний предел Функция f – подынтегральная функция х – переменная интегрирования

Формула Ньютона - Лейбница Если F – первообразная для f на [a; b], то

Пример Вычислить