Презентация на тему: Десятичные и натуральные логарифмы

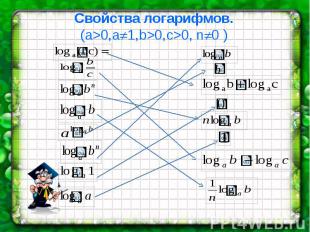
Свойства логарифмов. (а>0,a 1,b>0,c>0, n 0 )

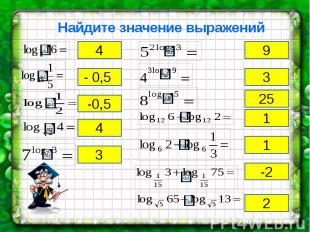
Найдите значение выражений

Решите уравнение

Тренировочный тест 1.Вычислить: 0,3log0,32 – 5 – 4,91; 2) – 4,7; 3) – 3; 4) 2. 2. Найдите значение выражения: log216 + log22 1) 4; 2) 5; 3) 6; 4) 4,5. 3.Найдите значение выражения : log0,39 -2log0,310 1) 2; 2) 1; 3) – 2; 4) 90. 4. Найдите x : lgx = 1/2lg9 – 2/3lg8 1) 3/4; 2) 4/3; 3) 3/2; 4) 6. 5. Упростите выражение: 32+log315 1) 17; 2) 135; 3) 225; 4) 30.

Проблема Обратите внимание - действия с логарифмами возможны только при одинаковых основаниях! А если основания разные!?

Переход к другому основанию Теорема Пусть дан логарифм loga b. Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство: В частности, если положить c = b, получим:

Десятичным логарифмом называется  логарифм по основанию 10. Он обозначается  lg , т.е. log 10 m = lg т Натуральным логарифмом называется  логарифм по основанию  е. Он обозначается  ln , т.е. log e m = ln m. Число е является иррациональным, его приближённое значение 2.718281828.

2) Найдите значение выражения

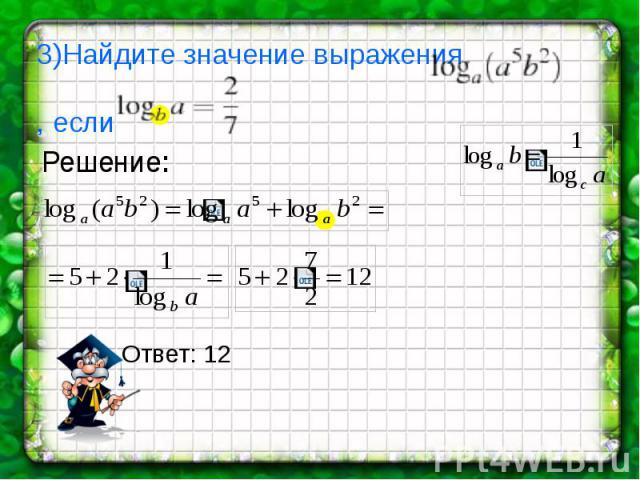
3)Найдите значение выражения , если Решение:

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году, хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой

Происхождение термина натуральный логарифм Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60. loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. .

е=2,718281828459045235360…. Саму константу впервые вычислил швейцарский математик Бернулли в ходе решения задачи о предельной величине процентного дохода. Бернулли показал, что процентный доход в случае сложного процента имеет предел: и этот предел равен 2,71828…

Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой.

Таблицы логарифмов Первые таблицы логарифмов были составлены швейцарским математиком Бюрги в 1590 году. Немного позднее таблицы логарифмов также составил шотландский ученый Непер. Непер брал за основание логарифма число, очень близкое к единице но меньшее, чем единица. Непер опубликовал свои таблицы в 1614, а Бюрги в 1620 году.

1 группа

Домашнее задание 1. Найдите 2. Вычислите:

Источники информации Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений/[Ш.А. Алимов, Ю.М. Колягин]; – М.: Просвещение, 2007. Открытый банк заданий для подготовки к ЕГЭ по математике www.mathege.ru Википедия. Натуральный логарифм. http://ru.wikipedia.org/wiki/%D0%9D%D0%B0%D1%82%D1%83%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BB%D0%BE%D0%B3%D0%B0%D1%80%D0%B8%D1%84%D0%BC ВикипедиЯ. е(число). http://ru.wikipedia.org/wiki/E_%28%D1%87%D0%B8%D1%81%D0%BB%D0%BE%29 Эйлер. http://ru.wikipedia.org/wiki/%D0%AD%D0%B9%D0%BB%D0%B5%D1%80,_%D0%9B%D0%B5%D0%BE%D0%BD%D0%B0%D1%80%D0%B4 Бернулли. http://ru.wikipedia.org/wiki/%D0%91%D0%B5%D1%80%D0%BD%D1%83%D0%BB%D0%BB%D0%B8,_%D0%AF%D0%BA%D0%BE%D0%B1 Неппер. http://a-nomalia.narod.ru/100otkr/45.htm Фон презентации http://tatyana-chulan.ucoz.ru/forum/8-13-2