Презентация на тему: Числовые последовательности

Урок-конференция «Числовые последовательности»

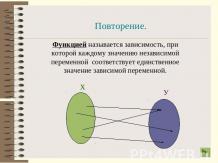
Числовые последовательности Функцию вида y=f(x), где xєΝ, называют функцией натурального аргумента или числовой последовательностью и обозначают y=f(n) или y₁, y₂, y₃ …

Способы задания Аналитическое задание числовой последовательностиСловесное задание последовательностиРекуррентное задание последовательности

Арифметическая прогрессия Числовую последовательность, каждый член которой начиная со второго равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, число d – разностью арифметической прогрессии.

Арифметическая прогрессия а₁, a₂, a₃, … an , …an = an -1 + dаn = а₁ + (n – 1)·dSn = a₁ + a₂ + … + anSn = n·(a₁ + an) / 2Sn = n·(2a₁ + (n1)d) / 2аn = (an1 + an+1) / 2

Геометрическая прогрессия Числовая последовательность, все члены которой отличны от нуля и каждый член которой начиная со второго равен предыдущему члену умноженному на одного и того же числа q, называется геометрической прогрессией, число q – знаменатель геометрической прогрессии.

Геометрическая прогрессия b₁, b₂, b₃, … bn , …bn = bn -1 · q, (b₁≠0, q≠0)bn = b 1 · qⁿ⁻¹Sn = b₁ + b₂ + … + bnSn = b₁ ·(qⁿ 1) ⁄ (q 1)bn²=bn1 · bn+1