Презентация на тему: Исследования по теории показателей А.М. Ляпунова

Исследования по теории показателей А.М. Ляпунова Научная школа В.М. Миллионщикова:И.Н. Сергеев, А.Н. Ветохин, В.В. БыковКафедра дифференциальных уравненийМеханико-математический факультет Московский государственный университет имени М.В.Ломоносова

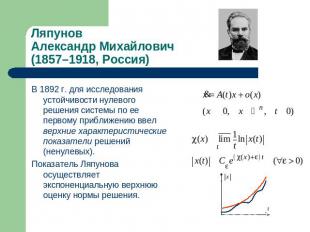
Ляпунов Александр Михайлович (1857–1918, Россия) В 1892 г. для исследования устойчивости нулевого решения системы по ее первому приближению ввел верхние характеристические показатели решений (ненулевых). Показатель Ляпунова осуществляет экспоненциальную верхнюю оценку нормы решения.

А.М. Ляпунов (1857–1918, Россия) Доказал, что в случае правильной (в частности, автономной) системы первого приближения верно следующее: если показатели всех ее решений отрицательны, то имеет место экспоненциальная устойчивость;если показатель хотя бы одного ее решения положителен, то имеет место неустойчивость.

А.М. Ляпунов (1857–1918, Россия) Изучил показатели всех решений n-мерной линеаризованной системы (с ограниченными коэффициентами): всего их оказалось ровно n (с учетом кратности);показатель с номером i отвечает за условную i-устойчивость (с начальными значениями из i-мерного многообразия);если система автономна, то показатели Ляпунова совпадают с действительными частями собственных значений ее матрицы.

Перрон Оскар (1880–1975, Германия) В 1913 г. привел пример точки разрыва старшего показателя Ляпунова системы как функции от ее коэффициентов. В результате встал вопрос об описании точек непрерывности (полунепрерывности сверху или снизу) показателей Ляпунова, рассматриваемых: как функционалы на пространстве линейных систем (с равномерной топологией); как функции параметра, задающего семейство систем (или на пространстве линейных систем с компактно-открытой топологией).

Виноград Роберт Эльюкимович (1924, Россия, Израиль) В 1957 г. ввел (задал формулами) центральные показатели, доказав, что они оценивают сдвиги показателей Ляпунова при равномерно малых возмущениях коэффициентов линейной системы: верхний — оценивает сдвиги вверх старшего показателя Ляпунова;нижний — оценивает сдвиги вниз младшего показателя Ляпунова.

МиллионщиковВладимир Михайлович(1939–2009, Россия ) В 1969 г. с помощью своего метода поворотов:доказал достижимость (обратную оценку) центральных показателей показателями Ляпунова при равномерно малых возмущениях коэффициентов линейной системы;описал все точки непрерывности всех одновременно показателей Ляпунова линейных систем;описал все точки грубой непрерывности (в целой окрестности) всех одновременно показателей Ляпунова линейных систем (это системы с интегральной разделенностью); доказал, что точки грубой непрерывности показателей всюду плотны в пространстве всех систем.

ИзобовНиколай Алексеевич(1940, Белоруссия) Для старшего показателя Ляпунова: в 1976–77 гг. в двумерном случае вычислил его миноранту (аналог нижнего центрального показателя), описав тем самым все точки его полунепрерывности снизу;в 1978 г. в n-мерном случае оценил его миноранту снизу.

СергеевИгорь Николаевич(1954, Россия ) Для каждого показателя Ляпунова в отдельности: в 1980 г. вычислил его мажоранту (аналог верхнего центрального показателя), описав тем самым все точки его полунепрерывности сверху;в 1993 г. в трехмерном случае вычислил его миноранту, описав тем самым и все точки его полунепрерывности снизу.

Бэр Рене-Луи (1874–1932, Франция) В 1899 г. предложил свою классификацию разрывных функций: нулевой класс Бэра состоит из непрерывных функций;если функция представляется, как поточечный предел последовательности функций нулевого класса, то она принадлежит первому классу Бэра;если функция представляется, как поточечный предел последовательности функций первого класса, то она принадлежит второму классу Бэра; и т. д.

В.М. Миллионщиков(1939–2009, Россия ) С 1980 г. начал применять теорию разрывных функций Бэра к показателям линейных систем, доказав принадлежность:каждого показателя Ляпунова — 2-му классу Бэра в равномерной и компактно-открытой топологиях;центральных показателей в компактно-открытой топологии:верхнего — 2-му классу Бэра, нижнего — 3-му классу Бэра(в равномерной топологии оба принадлежат 1-му классу Бэра).

Рахимбердиев Марат Исимгалиевич (1945–2008, Казахстан) В 1982 г. доказал, что показатели Ляпунова не принадлежат 1-му классу Бэра (ни в равномерной, ни тем более в компактно-открытой топологии) — отсюда стало ясно, что они принадлежат в точности 2-му классу Бэра.

Ветохин Александр Николаевич(1971, Россия) В 1995 г.:предложил простые признаки непринадлежности показателей 1-му классу Бэра в разных топологиях;доказал, что для всех показателей Ляпунова в компактно-открытой топологии: мажоранты не принадлежат 1-му классу Бэра,миноранты не принадлежат 2-му классу Бэра.

БыковВладимир Владиславович(1973, Россия) В 1996 г. доказал, что в компактно-открытой топологии миноранта старшего показателя Ляпунова принадлежит 3-му классу Бэра (тем самым — в точности 3-му).Этот результат: ранее был установлен лишь в трехмерном случае (И.Н. Сергеев, 1995 г.) ;позднее был распространен на миноранты всех остальных показателей Ляпунова (Е.Е. Салов, 1999 г.).

О. Перрон (1880–1975, Германия) В 1930 г.: рассмотрел нижние характеристические показатели решений (ненулевых), которые:осуществляют нижние экспоненциальные оценки их нормы, в случае правильной системы совпадают с верхними; обнаружил, что количество различных нижних показателей решений одной n-мерной системы может быть больше n (уже при n=2).

Н.А. Изобов(1940, Белоруссия) Показал, что показатели Перрона (нижние) устроены гораздо сложнее, чем показатели Ляпунова (верхние): количество нижних показателей диагональной системы может достигать 2ⁿ –1 (1964 г.);множество нижних показателей решений двумерной системы может включать целый отрезок (1965 г.);нижние показатели почти всех решений одной системы одинаковы (1968 г.).Впоследствии было получено полное описание всех возможных множеств нижних показателей (Е.А. Барабанов, 1986 г.).

И.Н. Сергеев(1954, Россия) В 2004 г.:регуляризовал по Миллионщикову нижние характеристические показатели, получив ровно n показателей Перрона для любой n-мерной системы; указал мажоранту старшего и миноранту младшего показателей Перрона, которые совпадают с верхним и, соответственно, нижним центральными показателями (нижнепредельными).

И.Н. Сергеев(1954, Россия) В 2004 г. для линейных уравнений n-го порядка:ввел характеристическиечастоты решений (ненулевых), задающие среднее число нулей решения (на промежутке длины π); доказал, что спектр (множество различных значений) частот автономного уравнения 4-го порядка может содержать сколь угодно большое число значений. Оказалось, что спектр частот последнего уравнения может даже заполнять целый отрезок (А.Ю. Горицкий, 2008 г.).

И.Н. Сергеев(1954, Россия) В 2004 г., регуляризовав по Миллионщикову характеристические частоты, получил ровно n значений для любого уравнения n-го порядка и доказал, что они:в случае автономного уравнения совпадают с модулями мнимых частей корней характеристического многочлена;являются разрывными функциями коэффициентов уравнения.

И.Н. Сергеев(1954, Россия) В 2009–10 гг., рассмотрев решения (ненулевые) линейных систем: распространил на них понятие частоты, определив полную частоту решения;ввел показатель блуждаемости решения (связанный со средней скоростью его вращения); доказал, что полные частоты и показатели блуждаемости всех решений автономной системы совпадают с модулями мнимых частей собственных значений ее матрицы.

Различные показатели ляпуновского типа Показатели: верхние (Ляпунов); нижние (Перрон);степенные (Демидович);неправильности (Перрон, Гробман, Миллионщиков);центральные (Виноград);особые (Боль), генеральные (Персидский);экспоненциальные (Изобов);вспомогательные (Миллионщиков); блуждаемости, колеблемости (Сергеев).

Классы линейных систем Системы с ограниченными коэффициентами (основной класс).Системы с неограниченными коэффициентами.Постоянные, периодические.Приводимые, почти приводимые.Правильные, бирегулярные.Системы с интегральной разделенностью.Системы, отвечающие уравнениям.Управляемые, с обратной связью.Гамильтоновы.

Топологии и классы возмущений Топологии (на полуоси): равномерная;сходимости на компактах (компактно-открытая);интегральная;сходимости в среднем.Возмущения:экспоненциальные;бесконечно малые;заданного порядка малости;не выводящие из заданного класса систем.

Возможные темы научных работ по линейным системам Найти формулу для мажоранты старшего показателя Ляпунова двумерной системы с неограниченными коэффициентами.Предъявить двумерную систему без интегральной разделенности, но с грубо устойчивым старшим показателем Ляпунова.Существует ли такая трехмерная система, что для любой пары двумерных подпространств ее решений наибольший показатель Перрона в первом из них больше наименьшего ― во втором?Описать все возможные спектры полных частот или показателей блуждаемости произвольного уравнения третьего порядка. Существует ли характеристика вектор-функции, принимающая на решениях любой n-мерной системы не более n значений, совпадающих в случае автономной системы с мнимыми частями (по модулю) собственных значений ее матрицы?

Возможные темы научных работ по классам Бэра Какому классу Бэра принадлежит миноранта старшего показателя Ляпунова, рассматриваемая как функционал на пространстве систем с неограниченными коэффициентами с компактно-открытой топологией?Существует ли такое семейство систем, коэффициенты которых непрерывно зависят от вещественного параметра, что старший показатель Ляпунова, как функция параметра, не является полунепрерывным снизу ни в одной точке?Какому классу Бэра принадлежат частоты уравнения (не считая младшей)?Какому классу Бэра принадлежат показатели Перрона (не считая старшего)?

Учебники и монографии по теории показателей Ляпунова