Презентация на тему: Числовые функции и способы их задания

Числовые функциии способы их задания

Содержание: ВведениеЧисловые функцииКусочное задание функцииГрафик функции

Введение Явления природы тесно связаны друг с другом. В большинстве случаев законы, управляющие взаимозависимостью явлений, весьма сложны из-за тесного переплетения различных факторов. Но среди громадного многообразия явлений ученые выделили такие, в которых взаимосвязь величин настолько тесна, что, зная значение одной из них, можно узнать значение другой величины. Простейшие примеры таких взаимозависимостей дает гео-метрия. Например, зная дли-ну стороны квадрата или ра-диус круга, можно найти пло-щади этих фигур, зная длину стороны куба можно вычис-лить его объем, и т. д.

В физике также встречаются зави-симости между величинами, в ко-торых значение одной величины однозначно определяет значение другой величины. Например, зная промежуток времени, протекший с начала свободного падения, можно найти путь, пройденный за этот промежуток времени падающим телом.Будем называть зависимость величины у от величины х функциональной, если каждому рассматриваемому значению величины х соответствует определенное значение величины у. Поскольку после выбора единиц измерения значения величин выражаются числами, для изучения функциональных зависимостей между величинами применяют понятие числовой функции, т. е. изучают определенного вида зависимости между числами.

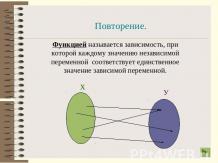
Числовые функции ОпределениеПусть Х – числовое множество. Правило, сопоставляющее каждому числу х из Х некоторое число у, называют числовой функцией, заданной на Х. Переменную, пробегающую множество Х, называют аргументом функции.Обычно аргумент функции обозначается буквой х.Сами числовые функции обозначаются буквами f, φ, g и т. д.Число b, которое функция f сопоставляет числу а Х , называют ее значением при х = а и обозначают f(a), b = f (a).С каждой функцией связано множество {f (x)|x X}. Его называют областью значений (или множеством значений) функции f и обозначают E (f).

Чтобы задать функцию f, надо указать ее область задания Х и правило, по которому каждому х Х сопоставляется число f (x). Обычно это правило дается в виде некоторого выражения, показывающего, какие операции нужно выполнить над х, чтобы получилось f (x). Для простоты функция, заданная на множестве Х некоторым выражением, обозначается тем же выражением с указанием множества Х. Если функция задана выражением на всей области существования этого выражения, ее обозначают лишь указанием выражения.Пример 1.Каждому b R и числовому множеству Х соответствует функция, зна-чение которой для любого х Х равно b. Такую функцию называют постоянной на Х.

Кусочное задание функцийИногда функции задают различными выражениями на разных участках.Пример 1.Парашютист прыгает из «зависшего» вертолета. Первые t1 секунд он падает свободно, а затем раскрывается пара-шют и t2 секунд падает до приземления с постоянной скоростью v. Выразите расстояние s парашютиста от вертоле-та как функцию времени t.

График функции Для наглядного изображения числовых функций используют ее графики. Каждой паре чисел (х; f (x)), х Х ставят в соответствие точку М (х; f (x)) координатной плоскости. Получившееся при этом множество точек называют графиком функции. Определение.Графиком числовой функции f, заданной на числовом проме-жутке Х, называют множество Г всех точек координатной плос-кости, имеющих вид М (х; f (x)), где х Х

Чаще всего графиком функции является некоторая линия на плоскости, быть может, распадающаяся на несколько кусков. Однако не всякая линия является графиком некоторой функции. Например, окружность не может быть графиком никакой функции, так как, зная абсциссу точки окружности, мы получаем, вообще говоря, два значения ординаты, а функция сопоставляет каждому

Для того чтобы линия Г была графиком некоторой функции, необходимо и достаточно, чтобы всякая прямая, параллельная оси ординат, либо не пересекалась с этой линией, либо пересекала ее в одной точке.Если функция f задана некоторым выражением, то для построения ее графика выбирают из Х несколько значений аргумента х1, … , хn, находят соответствующие значения функции f (х1), … , f (хn) и строят точки М1 (х1, f (х1)), … , Мn (xn, f (хn)). Эти точки принадлежат графику данной функции. Если графиком функции является более или менее гладкая линия, то соединяя полученные точки гладкой линией, получаем приближенное изображение (эскиз) искомого графика.

Не всегда график функции состоит из одного куска. Например, график функции [x] состоит из бесконечного множества промежутков единичной длины. Левый конец этих промежутков принадлежит им, а правый – нет.График очень удобное средство, чтобы получить общее представление о ходе изменения функции. Во многих случаях зависимость между физи-ческими величинами непосредственно задается с помощью графика, вы-черченного самопишущим прибором. Например, прибор термограф дает кривую, показывающую изменение температуры воздуха с течением времени.