Презентация на тему: Множественный регрессионный анализ

необъясненная часть значения у (или возмущение) Множественная регрессия – это уравнение связи с несколькими независимыми переменными: Множественный регрессионный анализ часть значения у, которая объяснена уравнением регрессии с несколькими факторами

Построение уравнения регрессии 1. Постановка задачи Данные наблюдений xpn … x2n x1n yn n … … … … … … xp2 … x22 x12 y2 2 xp1 … x21 x11 y1 1 xp … x2 x1 y По имеющимся данным n наблюдений за совместным изменением параметров y, xj и ((yi,xj,i); j=1, 2, ..., p; i=1, 2, ..., n) необходимо определить аналитическую зависимость ŷ = f(x1,x2,...,xp), наилучшим образом описывающую данные наблюдений. Критерий качества выбранной зависимости:

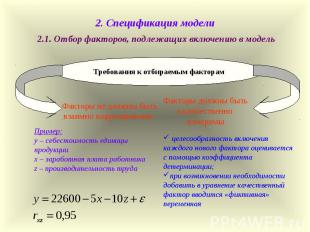
2.1. Отбор факторов, подлежащих включению в модель Требования к отбираемым факторам Факторы не должны быть взаимно коррелированы Факторы должны быть количественно измеримы целесообразность включения каждого нового фактора оценивается с помощью коэффициента детерминации; при возникновении необходимости добавить в уравнение качественный фактор вводится «фиктивная» переменная Пример: y – себестоимость единицы продукции x – заработная плата работника z – производительность труда 2. Спецификация модели

Парная коллинеарность и мультиколлинеарность Две переменные считаются явно коллинеарными, т.е. находятся между собой в линейной зависимости, если коэффициент интеркорреляции (корреляции между двумя объясняющими переменными) ≥ 0,7. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из уравнения. Мультиколлинеарность – линейная зависимость между более чем двумя переменными, т.е. совокупное воздействие факторов друг на друга.

Включение в модель мультиколлинеарных факторов нежелательно по следующим причинам: затрудняется интерпретация параметров множественной регрессии; параметры линейной регрессии теряют экономический смысл; оценки параметров не надежны, имеют большие стандартные ошибки и меняются с изменением количества наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Оценка мультиколлинеарности Для оценки мультиколлинеарности используется определитель матрицы парных коэффициентов интеркорреляции: (!) Если факторы не коррелируют между собой, то матрица коэффициентов интеркорреляции является единичной, поскольку в этом случае все недиагональные элементы равны 0. Например, для уравнения с тремя переменными

(!) Если между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0. Чем ближе к 0 определитель матрицы коэффициентов интеркорреляции, тем сильнее мультиколлинеарность и ненадежнее результаты множественной регрессии. Чем ближе к 1 определитель матрицы коэффициентов интеркорреляции, тем меньше мультиколлинеарность факторов.

Способы преодоления мультиколлинеарности факторов: исключение из модели одного или нескольких факторов; переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Например, если , то можно построить следующее совмещенное уравнение: переход к уравнениям приведенной формы (в уравнение регрессии подставляется рассматриваемый фактор, выраженный из другого уравнения).

2. Спецификация модели 2.2. Выбор формы уравнения регрессии Линейная регрессия Линеаризуемые регрессии Степенная регрессия Экспоненциальная регрессия Гиперболическая регрессия

Например, зависимость спроса на товар (Qd) от цены (P) и дохода (I) характеризуется следующим уравнением: Qd = 2,5 - 0,12P + 0,23 I. Коэффициенты данного уравнения говорят о том, что при увеличении цены на единицу, спрос уменьшится в среднем на 0,12 единиц, а при увеличении дохода на единицу, спрос возрастет в среднем 0,23 единицы. Например, зависимость выпуска продукции Y от затрат капитала K и труда L: говорит о том, что увеличение затрат капитала K на 1% при неизменных затратах труда вызывает увеличение выпуска продукции Y на 0,23%. Увеличение затрат труда L на 1% при неизменных затратах капитала K вызывает увеличение выпуска продукции Y на 0,81%.

или Отсюда получаем систему уравнений: 3. Оценка параметров модели 3.1. МНК

где ∆ – определитель системы: ∆a, ∆b1, ∆bp – частные определители (∆j) , которые получаются из основного определителя путем замены j-го столбца на столбец свободных членов Решение системы уравнений с помощью метода определителей:

3. Оценка параметров модели 3.2. Метод оценки параметров через стандартизованные коэффициенты β Уравнение регрессии в стандартизованном (нормированном) масштабе: где , - стандартизованные переменные β - стандартизованные коэффициенты регрессии. β-коэффициенты показывают, на сколько сигм (средних квадратических отклонений) изменится в среднем результат за счет изменения соответствующего фактора xi на одну сигму при неизменном среднем уровне других факторов.

или Параметр a определяется как: Коэффициенты β определяются при помощи МНК из следующей системы уравнений методом определителей: Взаимосвязь bi и β Связь коэффициентов «чистой» регрессии bi с коэффициентами βi описывается соотношением:

yi = ŷi + εi D(y) = D(ŷ) + D(ε) (остаточная) сумма квадратов отклонений, не объясненная регрессией + сумма квадратов отклонений, объясненная регрессией = полная (общая) сумма квадратов отклонений 4. Проверка качества уравнения регрессии Н0: уравнение статистически не значимо

где m – число независимых переменных в уравнении регрессии; n – число единиц совокупности. Если Fфакт > Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения. Если Fфакт < Fтабл, то Н0 не отклоняется и признается статистическая незначимость уравнения регрессии. F-критерий Фишера:

Частный F-критерий: - оценивает статистическую значимость присутствия каждого из факторов в уравнении.