Презентация на тему: Орнаменты. Уравнения орнаментов

Орнаменты. Уравнения орнаментов Презентацию выполнил Ученица 11 «А» класса МОУ СОШ №2 с.Нартан Канимготова Хусейна

Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математике. Герман Вейль (известный математик)

Орнамент – это узор, состоящий из ритмически упорядоченных элементов для украшения каких – либо предметов или архитектурных сооружений. Орнаменты с давних времен применяются в декоративном искусстве.

С другой стороны, при исследовании геометрического строения кристаллов выявилось, что их атомы расположены очень правильным образом, образуя как бы пространственный орнамент. На рисунке изображены проекции пространственных решеток граната, кварца и каменной соли.

Бесконечная плоская фигура Ф называется плоским орнаментом, если выполнены следующие условия: (1) среди перемещений, отображающих Ф на себя, существуют неколлинеарные параллельные переносы.(2) среди всех векторов (параллельных переносов), отображающих Ф на себя, существует вектор наименьшей длины.Если плоский орнамент Ф отображается сам на себя при поворотах вокруг точки А на углы, только кратные 360°/п, где п — натуральное число, большее 1, то точка А называется центром симметрии порядка п этого орнамента Ф.

Линейные орнаменты.Если плоская фигура отображается сама на себя при параллельных переносах только одного направления (и противоположному ему), причем среди этих переносов существует перенос наименьшей длины, то такая фигура называется линейным орнаментом - бордюром.

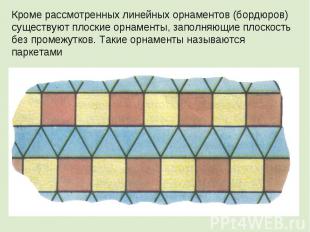
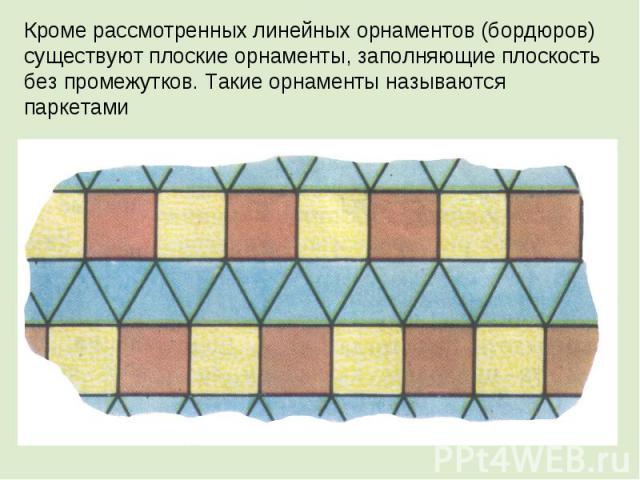
Кроме рассмотренных линейных орнаментов (бордюров) существуют плоские орнаменты, заполняющие плоскость без промежутков. Такие орнаменты называются паркетами

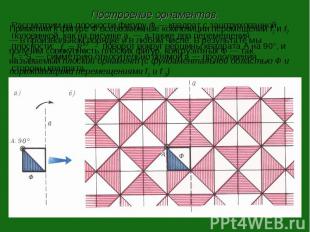
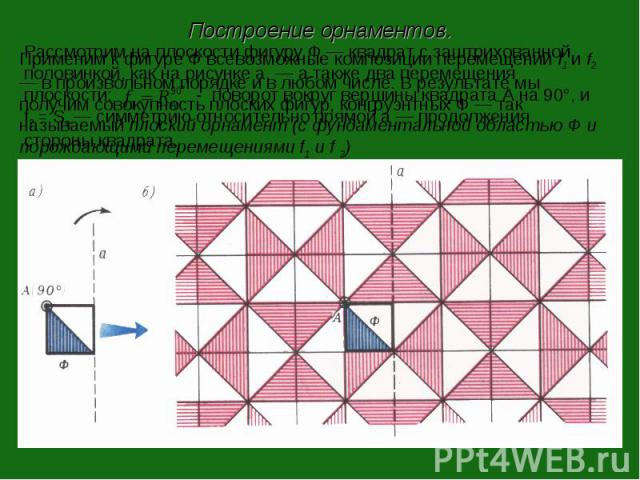
Построение орнаментов.Применим к фигуре Ф всевозможные композиции перемещений f1 и f2 — в произвольном порядке и в любом числе. В результате мы получим совокупность плоских фигур, конгруэнтных Ф — так называемый плоский орнамент (с фундаментальной областью Ф и порождающими перемещениями f1 и f 2)

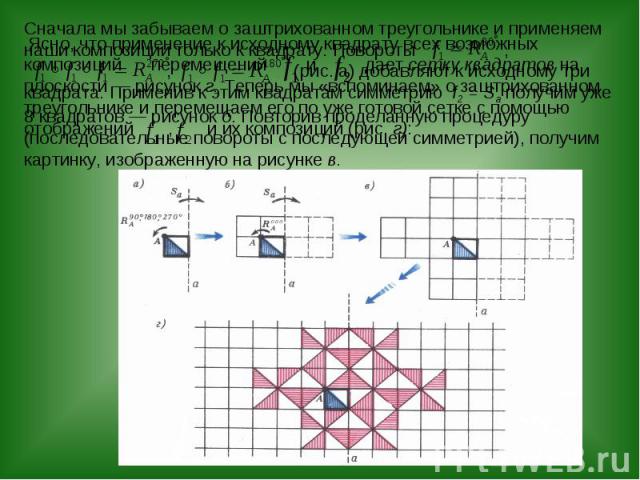
Ясно, что применение к исходному квадрату всех возможных композиций перемещений и дает сетку квадратов на плоскости — рисунок г. Теперь мы «вспоминаем» о заштрихованном треугольнике и перемещаем его по уже готовой сетке с помощью отображений , и их композиций (рис. г): Сначала мы забываем о заштрихованном треугольнике и применяем наши композиции только к квадрату. Повороты , , (рис. а) добавляют к исходному три квадрата. Применив к этим квадратам симметрию f2 = Sa получим уже 8 квадратов — рисунок б. Повторив проделанную процедуру (последовательные повороты с последующей симметрией), получим картинку, изображенную на рисунке в.

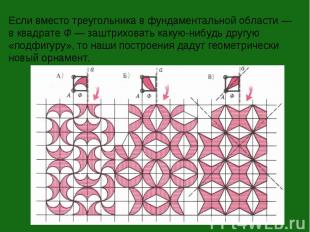
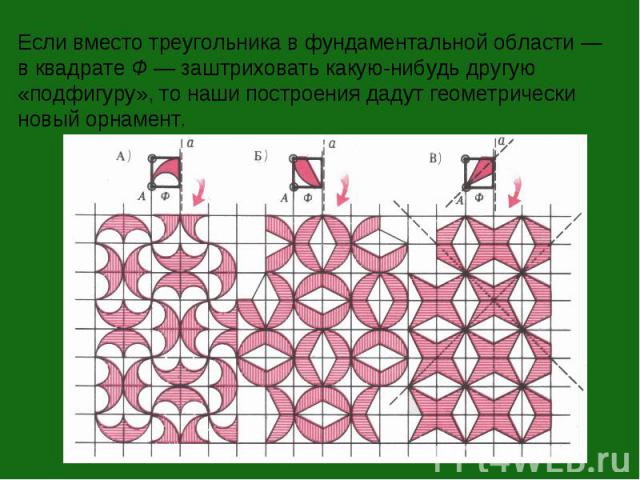
Если вместо треугольника в фундаментальной области — в квадрате Ф — заштриховать какую-нибудь другую «подфигуру», то наши построения дадут геометрически новый орнамент.

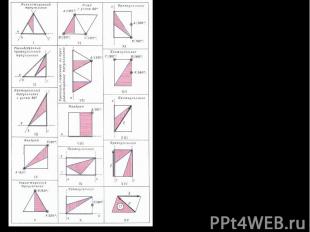
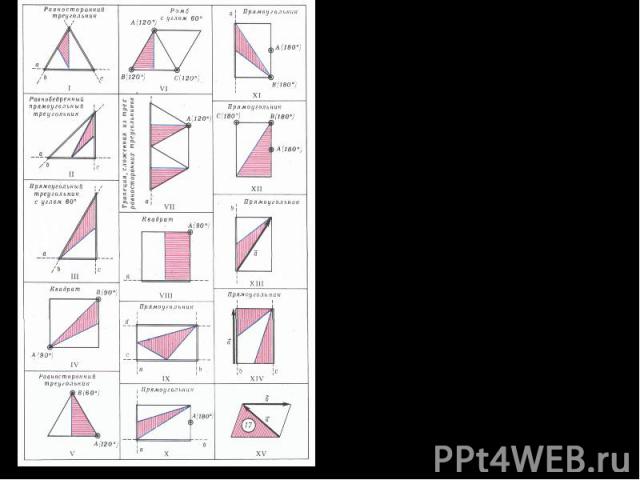
Это орнаменты разных типов: их группы симметрии устроены по-разному (имеют разные сетки осей симметрии или разные наборы порядков центров симметрии — разные «скелеты», — или же разные множества переносов). Начертив эти 15 орнаментов и их скелеты, можно подметить много интересных закономерностей.

Если добавить к этим орнаментам еще два, то получится полный «атлас» плоских орнаментов! Оказывается, существует только 17 различных типов орнаментов, или ровно 17 различно устроенных групп симметрии плоских орнаментов.

Уравнения орнаментов.Под математическим орнаментом мы будем понимать рисунок, характеризуемым каким – либо уравнением или неравенством (а может быть системой уравнений или системой неравенств), в котором многократно повторяется тот или иной узор.

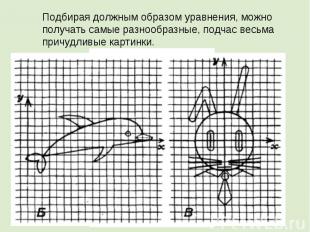
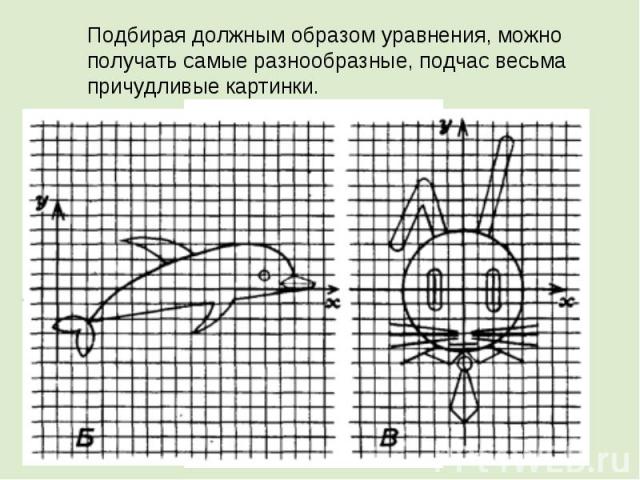
Подбирая должным образом уравнения, можно получать самые разнообразные, подчас весьма причудливые картинки.

Посмотрим как они получаются. Линейный орнамент получается с помощью переносов некоторой основной фигуры вдоль некоторого направления. Если сам линейный орнамент считать основной фигурой и произвести над ним серию переносов вдоль нового направления, то мы получим двумерный орнамент. Повороты основной фигуры на углы, кратные , приводят к круговому орнаменту.

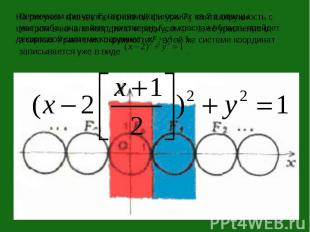
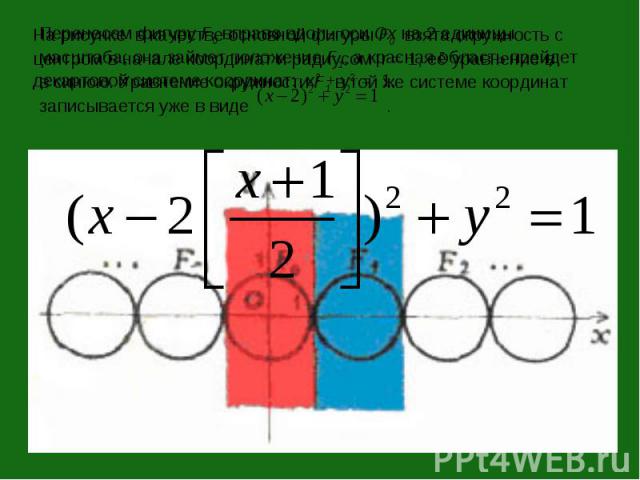
Перенесем фигуру F0 вправо вдоль оси Ox на 2 единицы масштаба; она займет положение F1, а красная область прейдет в синюю. Уравнение окружности F1 в той же системе координат записывается уже в виде .