![[α;b] – отрезок [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал](https://fs1.ppt4web.ru/images/95341/124520/640/img1.jpg "[α;b] – отрезок [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал")
![Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), такая, что Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), …](https://fs1.ppt4web.ru/images/95341/124520/640/img4.jpg "Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), такая, что Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), …")
![Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) , Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (…](https://fs1.ppt4web.ru/images/95341/124520/640/img6.jpg "Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) , Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (…")
Презентация на тему: Возрастание и убывание функции
![[α;b] – отрезок [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - по](https://fs1.ppt4web.ru/images/95341/124520/310/img1.jpg "[α;b] – отрезок [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - по")
[α;b] – отрезок [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал
x1 > x2 f(x1 ) > f(x2) x1 > x2 f(x1 ) > f(x2)
x1 > x2 f(x1 ) < f(x2) x1 > x2 f(x1 ) < f(x2)
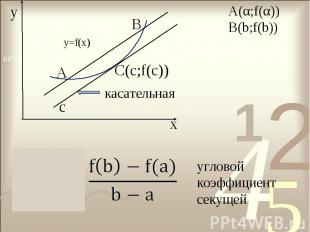
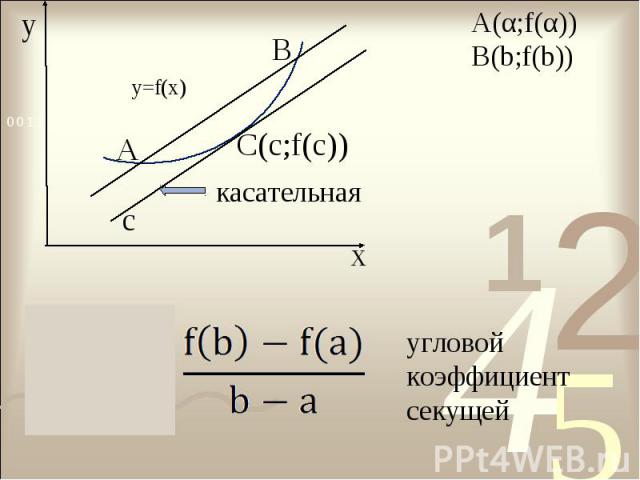
![Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α](https://fs1.ppt4web.ru/images/95341/124520/310/img4.jpg "Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α")
Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), такая, что Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), такая, что f(b) – f(α) = f ′(c) (b - α)
![Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α](https://fs1.ppt4web.ru/images/95341/124520/310/img6.jpg "Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α")
Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) , Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) , то функция f(x) возрастает на отрезке [α;b] , а если f′(x)<0 для всех х € (α;b) , то функция f(x) убывает на отрезке [α;b] .
