Презентация на тему: Возрастание убывание функции

Возрастание убывание функции Степенная функция Учитель математики Голубкова Елена ЮрьевнаГБОУ школа №135 Выборгского района г.Санкт-Петербурга 267-872-921

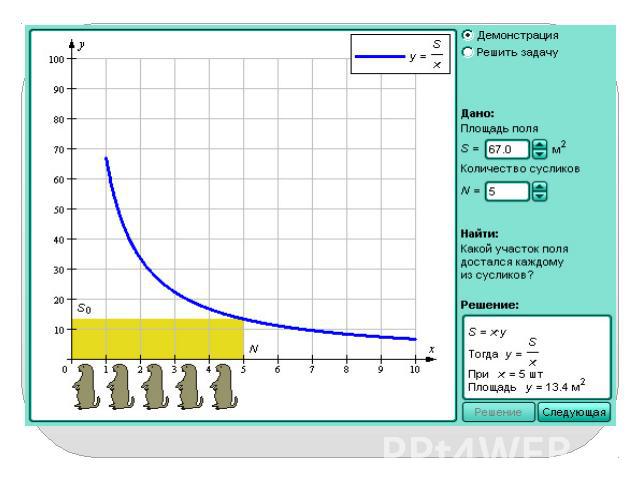
Цели и задачи урока1) Ввести понятие возрастающей, убывающей, постоянной функции. Привести примеры таких графиков2)Показать некоторые степенные функции3)Исследовать графики разных функций на возрастание и убывание4) Показать связь данных понятий с жизнью

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).

Функция называется постоянной (Const) если она не меняет значения функции при изменении аргумента

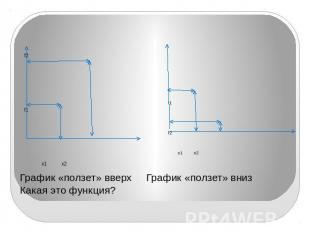
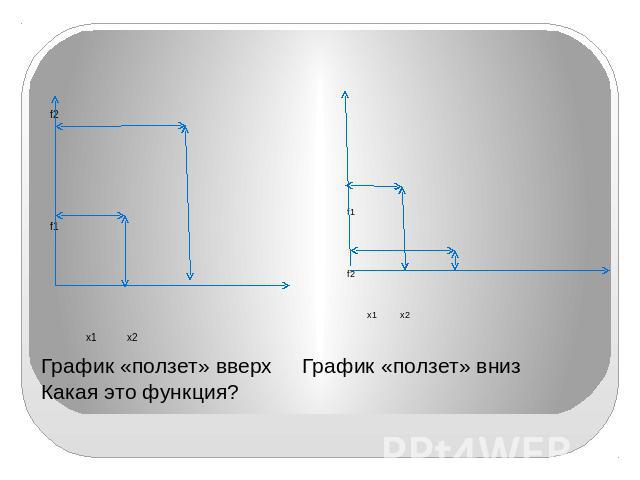
График «ползет» вверх График «ползет» вниз Какая это функция?

График расположен параллельно оси абсцисс

Промежутки возрастания и убывания функции. На показанном на рисунке графике функция y = f (x), возрастает на каждом из промежутков [a; x1] и [x2; b] и убывает на промежутке [x1; x2]. Обратите внимание, что функция возрастает на каждом из промежутков [a; x1] и [x2; b], но не на объединении их.

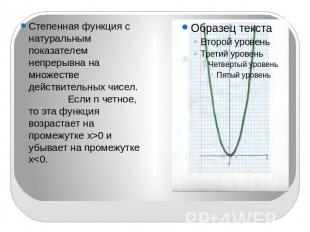
Степенная функция с натуральным показателем непрерывна на множестве действительных чисел. Если n четное, то эта функция возрастает на промежутке x>0 и убывает на промежутке x<0.

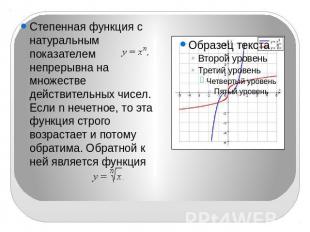
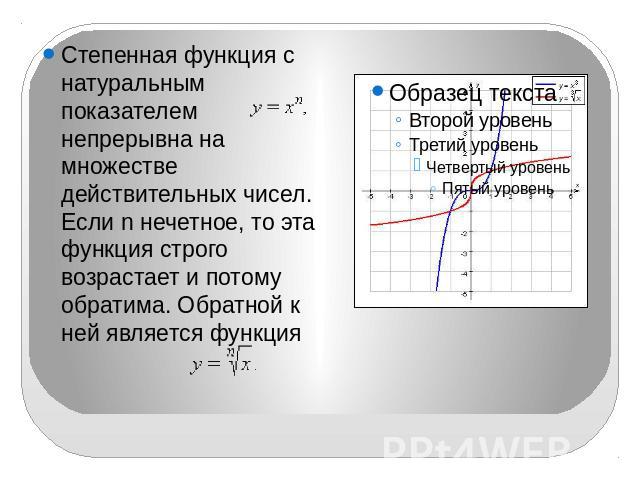
Степенная функция с натуральным показателем непрерывна на множестве действительных чисел. Если n нечетное, то эта функция строго возрастает и потому обратима. Обратной к ней является функция

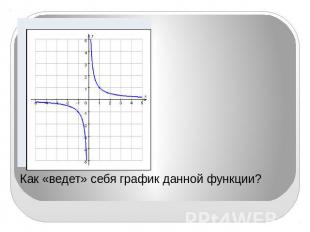
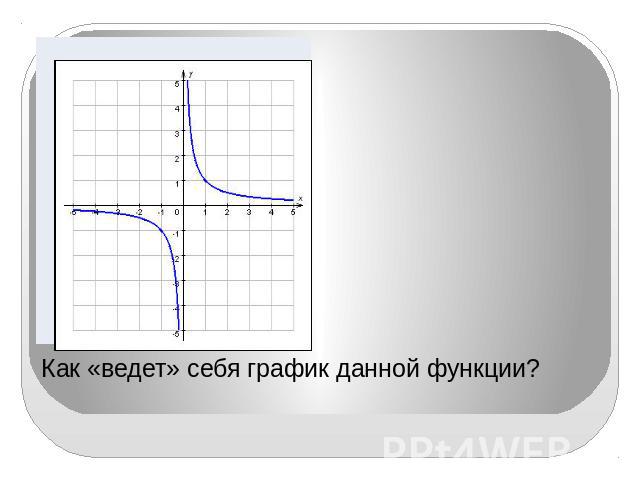
Как «ведет» себя график данной функции?

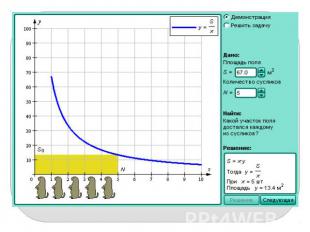
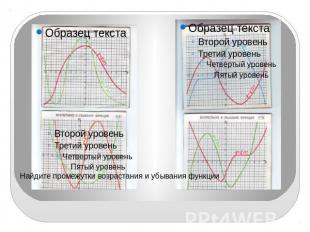
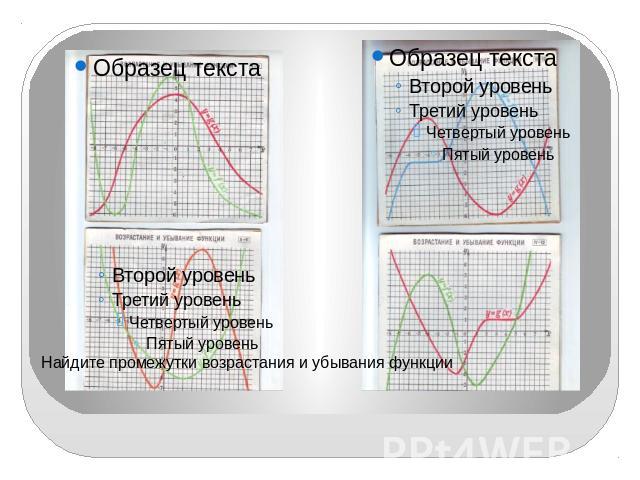
Найдите промежутки возрастания и убывания функции

1)С какими функциями мы «познакомились» ?2)Определите поведение изученных ранее функций (прямой, параболы, прямой пропорциональности)

Домашнее заданиеНачертите произвольный график функции и исследуйте его с точки зрения возрастания и убывания, свяжите его с конкретной жизненной ситуацией.

Спасибо всем.