Презентация на тему: Урок одной задачки

Кузьмина Н.А. заместитель директора по УВР, учитель математики ГБОУ Лицея № 387 имени Н.В.Белоусова Кировского района Санкт-Петербурга

Мотивация Система знаний Психологическая готовность

поиск разных способов решения этой задачи

Содержание задачи должно допускать вариативность решения. К уроку готовится общий для всех способов решения справочный материал. Данный прием наиболее эффективен на уроках обобщения и систематизации знаний, т.к. позволят не только закрепить новый материал, но и ещё раз вспомнить пройденный. Урок решения одной задачи не следует проводить слишком часто, проведение таких уроков наиболее оправдано раз в четверть, или в полугодие, а так же во время итогового повторения, т.к. именно тогда можно подобрать комбинированную задачу, при решении которой применялся бы большой объем знаний.

4. По окончании урока необходимо подвести итог, проанализировав какой из предложенных способов был наиболее рациональным, какой способ был более понятен каждому ученику, какие возникли проблемы, почему и т.д. 5. Данный прием с некоторыми изменениями можно использовать для организации самостоятельной работы дома. 6. Структура урока может меняться.

Постановка проблемы. Мозговой штурм. Распределение на группы. Работа в группах. Представление решений. Рефлексия. Домашнее задание.

Не все согласны, что важно научиться решать задачи несколькими способами, а как думаете вы?

1.Геометрический способ (определение угла между плоскостями) 2.Аналитический способ (метод координат) 3.Геометрический способ (свойство ортогональной проекции)

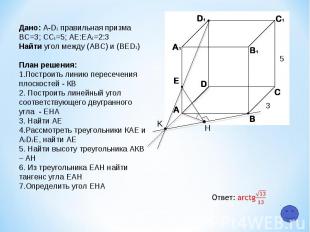
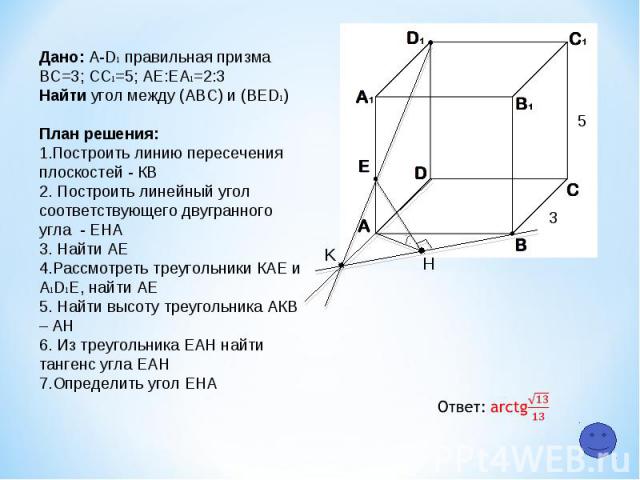
K H 5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС) и (ВЕD1) План решения: Построить линию пересечения плоскостей - КB 2. Построить линейный угол соответствующего двугранного угла - ЕНА 3. Найти АЕ 4.Рассмотреть треугольники КАЕ и А1D1E, найти АЕ 5. Найти высоту треугольника АКВ – AH 6. Из треугольника ЕАН найти тангенс угла ЕАН 7.Определить угол ЕНА

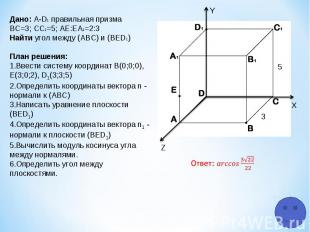
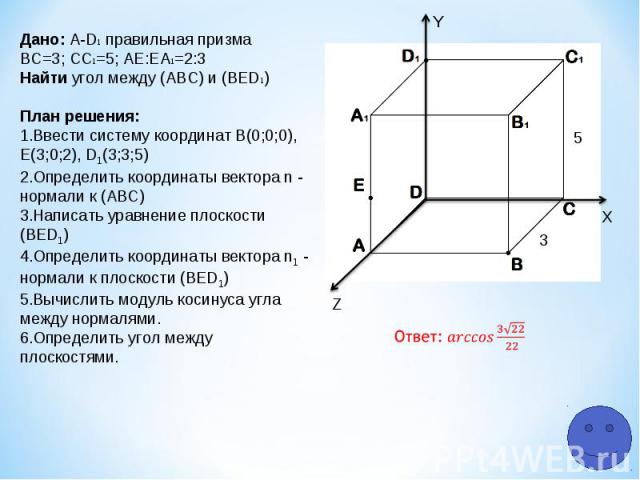
Z Y X 5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС) и (ВЕD1) План решения: Ввести систему координат В(0;0;0), Е(3;0;2), D1(3;3;5) Определить координаты вектора n - нормали к (АВС) Написать уравнение плоскости (ВЕD1) Определить координаты вектора n1 - нормали к плоскости (ВЕD1) Вычислить модуль косинуса угла между нормалями. Определить угол между плоскостями.

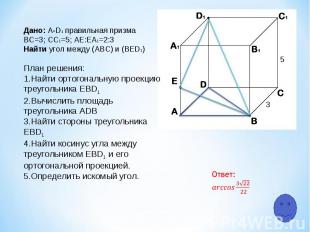
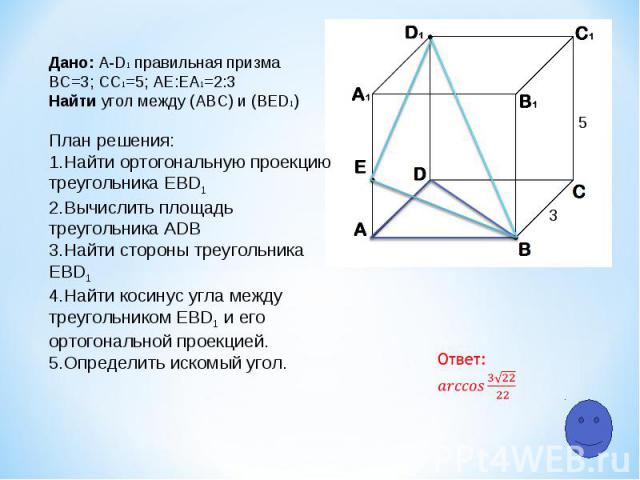
5 3 Дано: A-D1 правильная призма ВС=3; СC1=5; АЕ:ЕA1=2:3 Найти угол между (АВС) и (ВЕD1) План решения: Найти ортогональную проекцию треугольника ЕВD1 Вычислить площадь треугольника ADB Найти стороны треугольника ЕВD1 Найти косинус угла между треугольником ЕВD1 и его ортогональной проекцией. Определить искомый угол.

Отобрать необходимый теоретический материал (подсказка 1 уровня) Составить план решения задачи (подсказка 2 уровня) Оформить подробное решение задачи (подсказка 3 уровня)

Какой из представленных путей решения вам показался наиболее рациональным, почему? Какой способ, по-вашему наиболее понятен? Какие возникли затруднения при решении задачи?

Обязательный уровень: Записать подробное решение задачи тремя способами Тренировочный уровень: Решить задачу несколькими способами: В правильной треугольной призме ABCDA1B1C1D1 все рёбра которой равны 1, найти тангенс угла между плоскостями ABC и CA1B1. (ответ 2√3/3)

Творческое задание: Решить задачу. Создать к задаче подсказки трёх уровней: 1.ВСПОМНИ (перечень необходимых теоретических фактов) 2.РЕШИ (План решения) 3.ПРОВЕРЬ (Подробное решение задачи) Оформить творческое задание в виде презентации