Презентация на тему: Угол между плоскостями

Угол между плоскостями Решение задач уровня С.


Аргументы 1. Определение куба. 2. Определение правильной призмы. 3. Свойства правильной призмы. 4. Свойство средней линии треугольника. 5. Признак параллельности плоскостей. 6. Определение угла между плоскостями. 7. Линейный угол двугранного угла. 8. Теорема Пифагора. 9. Теорема косинусов.
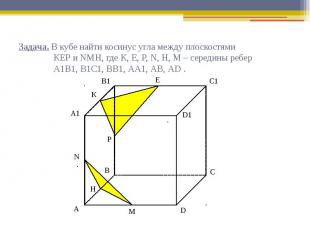
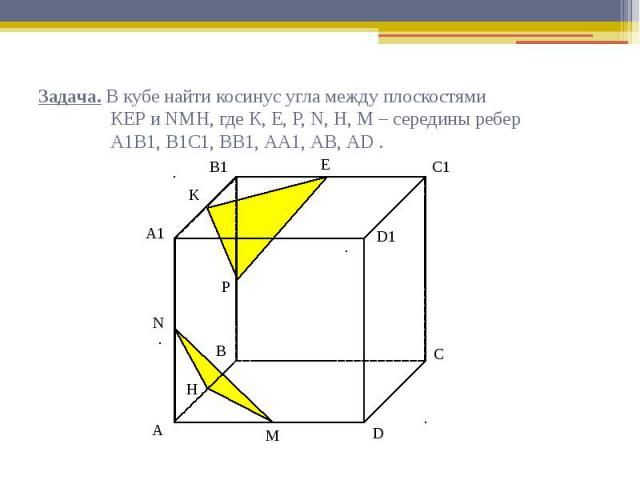
Задача. В кубе найти косинус угла между плоскостями КЕР и NМН, где К, Е, Р, N, Н, М – середины ребер А1В1, В1С1, ВВ1, АА1, АВ, АD .
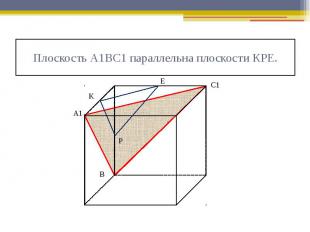
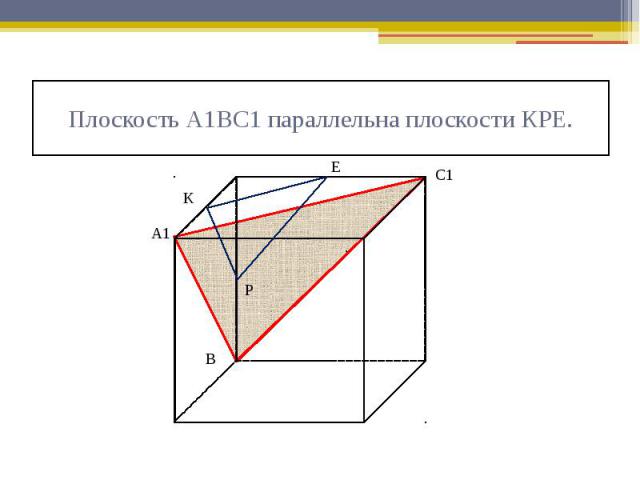
Плоскость А1ВС1 параллельна плоскости КРЕ.

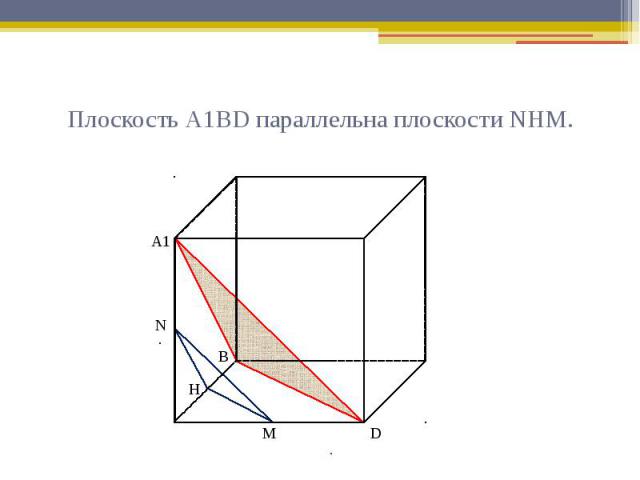
Плоскость А1ВD параллельна плоскости NНМ.

А1ВС1 пересекается с А1ВD1 по прямой А1В.

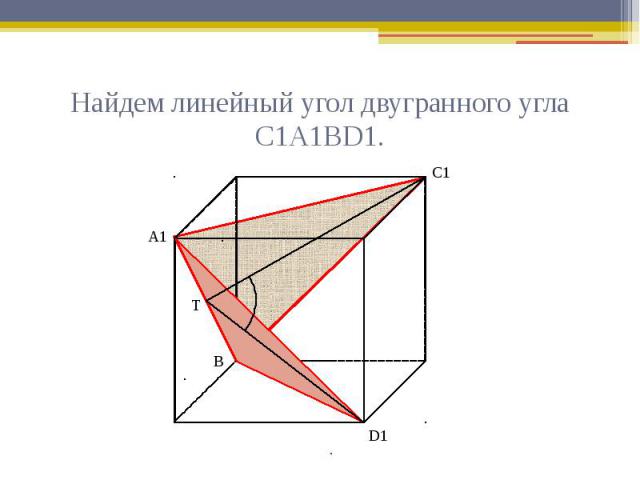
Найдем линейный угол двугранного угла С1А1ВD1.
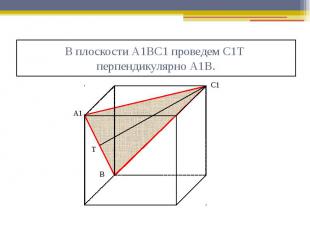
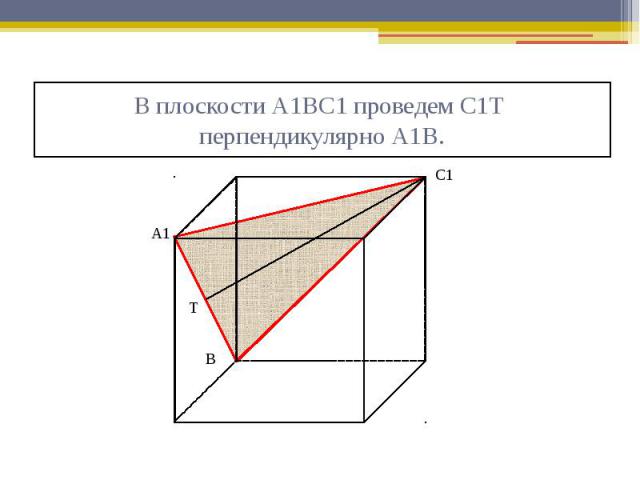
В плоскости А1ВС1 проведем С1Т перпендикулярно А1В.

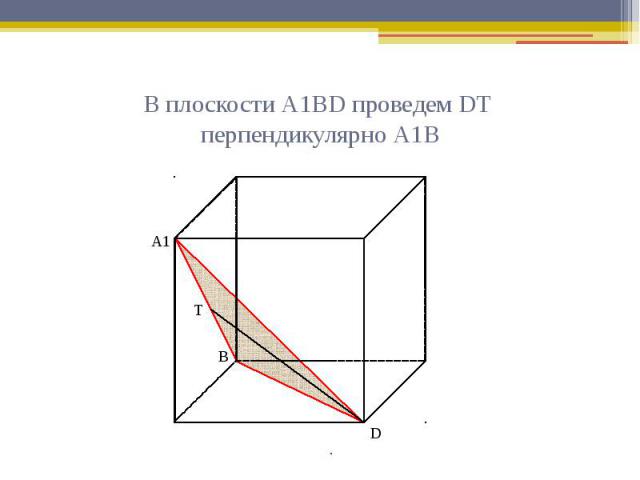
В плоскости А1ВD проведем DТ перпендикулярно А1В
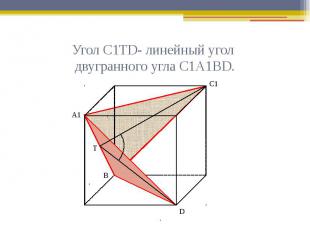
Угол С1ТD- линейный угол двугранного угла С1А1ВD.

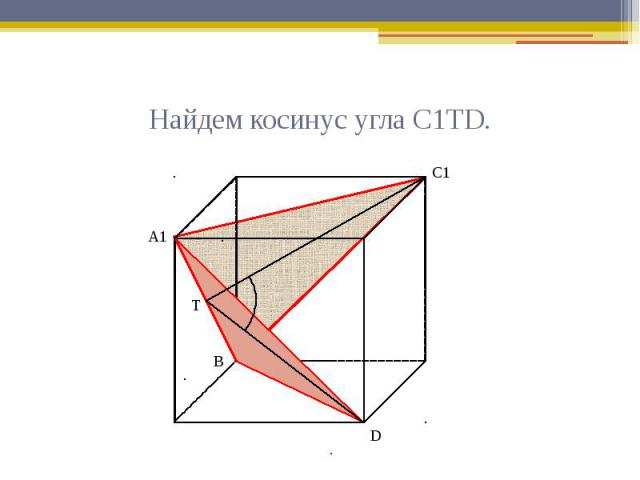
Найдем косинус угла С1ТD.
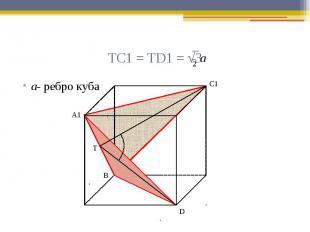
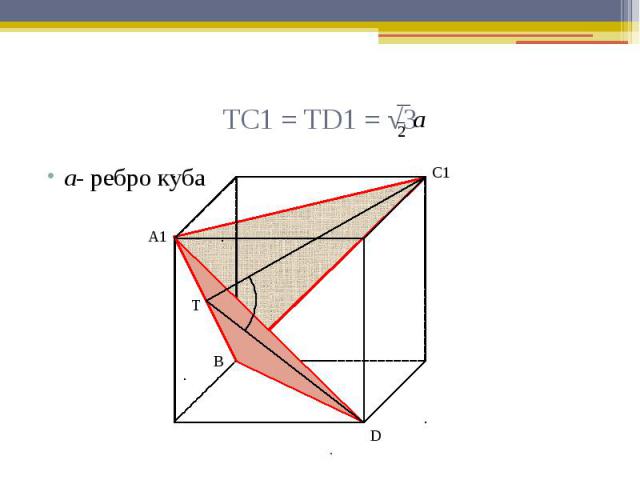
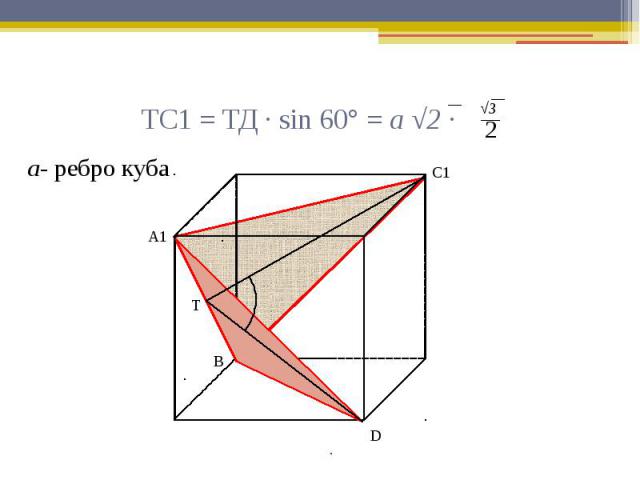
ТС1 = ТD1 = √3 а- ребро куба
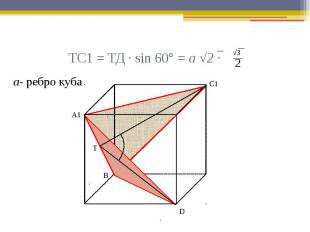
ТС1 = ТД · sin 60° = а √2 ·
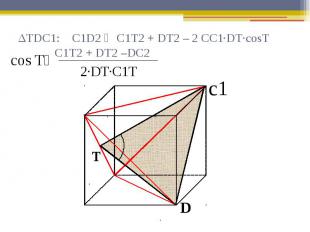
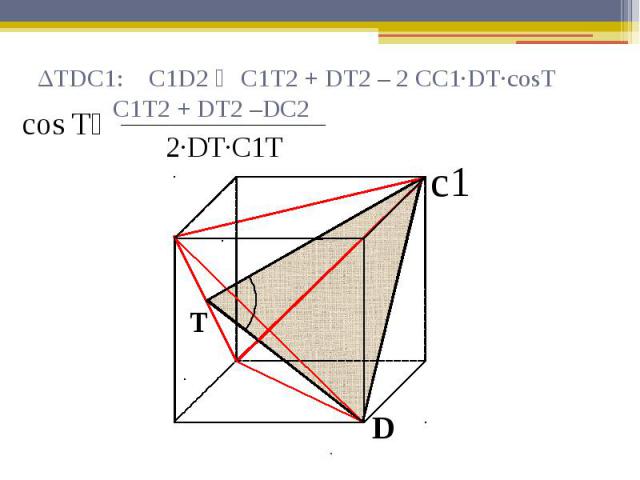
ΔTDC1: C1D2 ₌ C1T2 + DT2 – 2 CC1∙DT∙cosT C1T2 + DT2 –DC2

Находим cos T: сosT₌

Спасибо за внимание.