Презентация на тему: Транспортные задачи и задачи о назначениях

Лекция 5. Транспортные задачии задачи о назначениях Содержание лекции:Формулировка транспортной задачиМетод потенциаловОсобенности решения открытой транспортной задачиЗадача о назначениях

Литература Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — раздел 3.2.Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – 2-е изд. М.: Финансы и статистика, 2005. — раздел 2.2.6.Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.

5.1. Формулировка транспортной задачи Дано:Множество I, включающее m пунктов отправления груза, имеющегося в количествах ai (i=1…m)Множество J, включающее n пунктов потребления, в каждом из которых имеется спрос на данный груз в количестве bj (j=1…n)Затраты cij на перевозку единицы груза между пунктами i и jНайти:План перевозок X = (xij), согласно которому груз из пунктов отправления перевозится в пункты потребления с минимальными издержками, а спрос удовлетворяется полностьюОбычно предполагается, что общий размер запасов груза равен спросу (закрытая транспортная задача).При этом условии задача всегда имеет оптимальное решение.

Математическая запись

Получившаяся задача имеет форму задачи линейного программированияЕё можно решить симплексным методомОднако есть более эффективные способы её решения

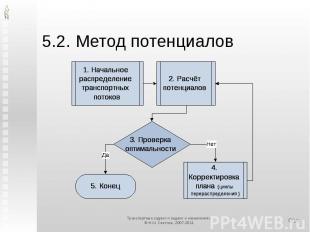
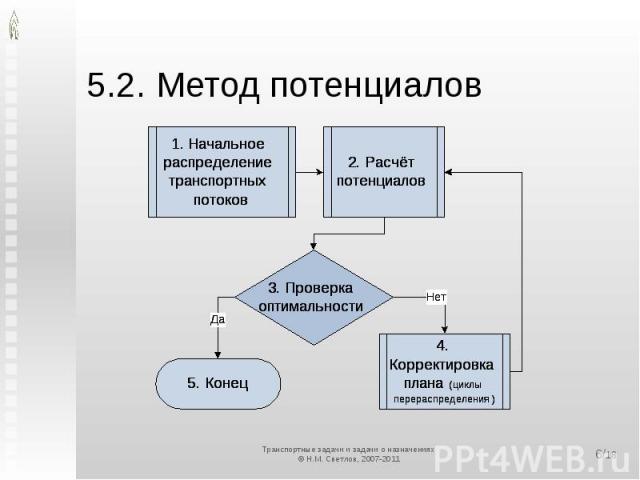
5.2. Метод потенциалов

5.2.1. Начальное распределение транспортных потоков Теоретическая основаРанг матрицы ограничений транспортной задачи равен n+m–1 В оптимальном плане все переменные, кроме n+m–1, будут свободнымиСледовательно, равными нулюМетод северо-западного углаНе использует данных о затратахОбычно приводит к распределению, требующему много корректировокЗато самый простой

Начальное распределение получено!

5.2.2. Расчёт потенциалов Теоретическая основаПотенциалы приписываются поставщикам (ui) и потребителям (vj).Уравнение потенциаловcij = vj – ui Расчёт потенциалов:подобрать такие vj и ui, чтобы уравнение потенциалов выполнялось для всех базисных клеток (перевозок)

5.2.2 i = 1; ui = 0В строке i находим множество столбцов J’ с ненулевыми перевозками и нерассчитанными потенциаламиДля всех j J’ выполняемvj ui + cijВ столбце j находим множество строк I’ с ненулевыми перевозками и нерассчитанными потенциалами.Для всех i I’ выполняемui vj – cijВыполняем (2)Процесс закончен, когда I’ или J’ оказывается пустымРасчёт потенциалов завершён!

5.2.3. Проверка оптимальности Теоретическая основаПо используемым перевозкам cij разница в «ценах» (потенциалах) у потребителя j и у поставщика i равна стоимости перевозкиэто следует из способа расчёта потенциаловНеиспользуемая перевозка cij выгодна, если разница в «ценах» (потенциалах) у потребителя j и у поставщика i больше стоимости перевозкиУсловие оптимальностиРазница в потенциалах потребителя и поставщика по всем неиспользуемым перевозкам не больше стоимости перевозки

5.2.3 Условие оптимальностиРазница в потенциалах потребителя и поставщика по всем неиспользуемым перевозкам не больше стоимости перевозкиВ нашем примере выполняется не по всем неисп. перевозкамВыполняется только для 1 2.Значит, требуется переход к п.4. – корректировка плана

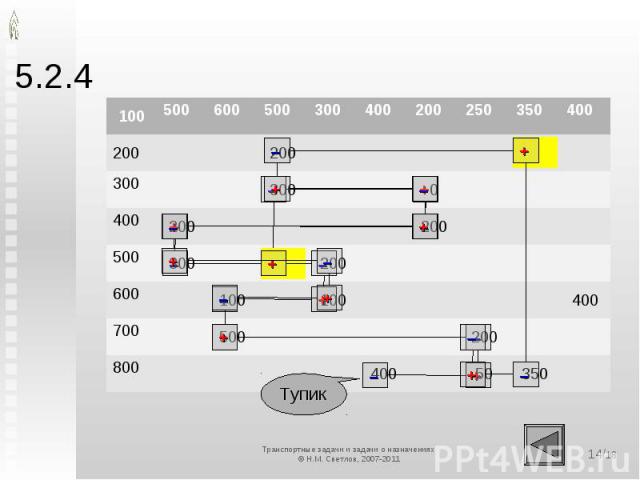
5.2.4. Корректировка плана Выбираем клеткус превышением разности потенциалов потребителя и поставщика над стоимостью транспортировкикак правило, с наибольшимСтроим контур (см. схему), начиная с данной клеткиПомечаем вершины контура знаками + и –начинаем со знака + в выбранной свободной клеткеНаходим наименьшую из величин в клетках со знаком –Вычитаем её из всех клеток «–» и прибавляем ко всем клеткам «+»Одну из клеток, в которых оказался нуль, объявляем свободной.Переходим к проверке критерия оптимальности

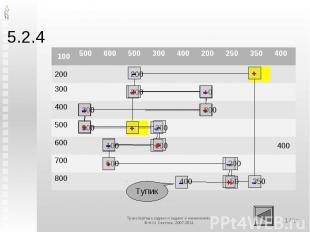
5.2.4

5.2.4 ОСОБЕННОСТИКонтур можно построить всегда, но не всегда удаётся угадать правильный путьВ больших задачах отыскание циклов вручную может оказаться проблематичнымДля компьютерных программ это не составляет проблемыКонтур может оказаться вырожденнымТак случается, если наименьшим значением в клетке со знаком – оказывается нульПересчёт по такому циклу не улучшает план, вследствие чего метод может зациклитьсяв этом случае выбирают другую свободную клетку в качестве начальнойЕсли после пересчёта получились нули в нескольких клетках, в качестве свободной можно выбрать любую из нихОстальные считаются базисными с нулевым объёмом перевозки

5.3. Особенности решения открытой транспортной задачи

5.4. Задача о назначениях Дано:n работниковn работдобавленная стоимость, создаваемая работником i на работе jНайти:оптимальное назначение работников на работы, максимизирующее добавленную стоимость

5.4 Переформулируется в транспортную задачу по следующему правилу:имеется n поставщиков, располагающих единичными ресурсами работникиимеется n потребителей с единичным спросом работыстоимость перевозок равна добавленной стоимости, взятой со знаком «минус»это делается для того, чтобы добавленная стоимость максимизироваласьРешается методом потенциалов, как обычно«Перевозки единичного объёма груза» интерпретируются как назначение работника i на работу jВсе базисные переменные в этом случае могут принимать только единичные значения