Презентация на тему: Стратегия игры. Решение задач методом «ГРАФЫ»

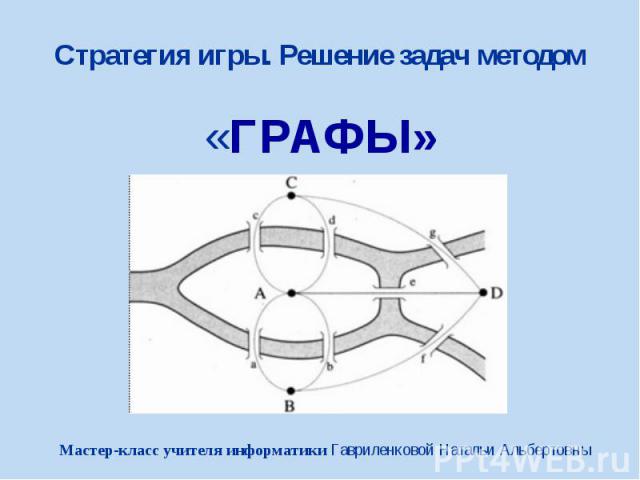
Стратегия игры. Решение задач методом «ГРАФЫ»

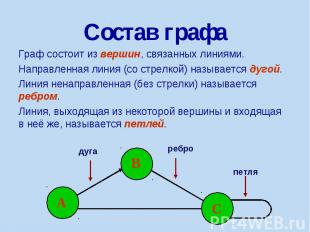
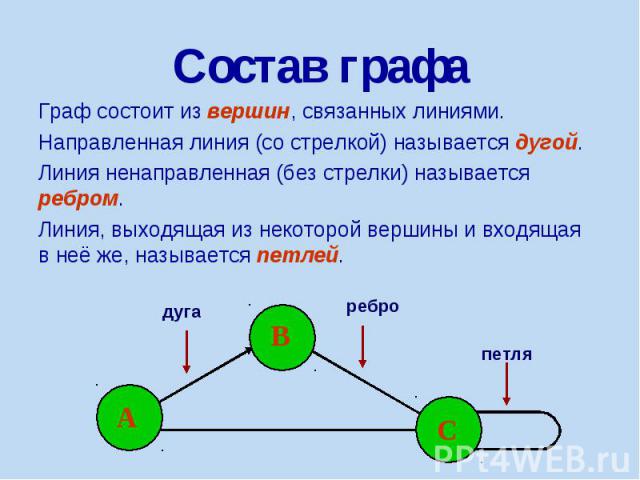
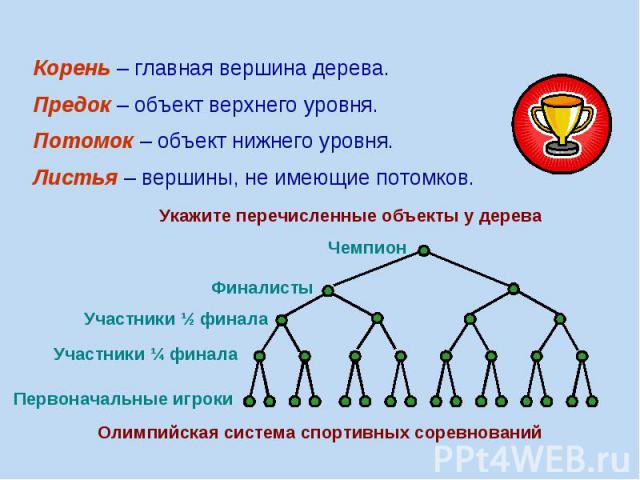
Состав графа Граф состоит из вершин, связанных линиями. Направленная линия (со стрелкой) называется дугой. Линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в неё же, называется петлей.

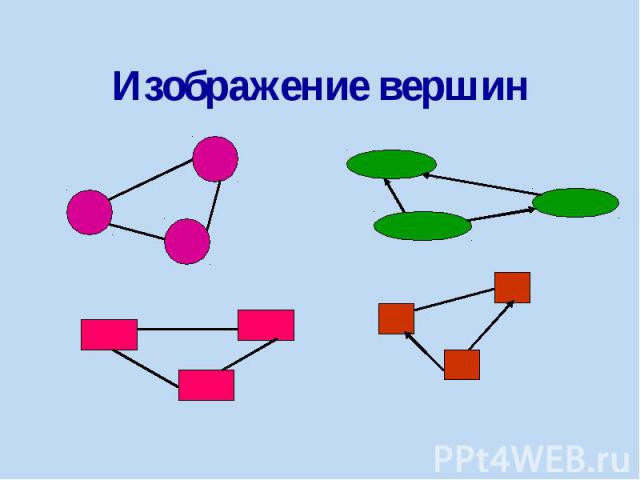
Изображение вершин

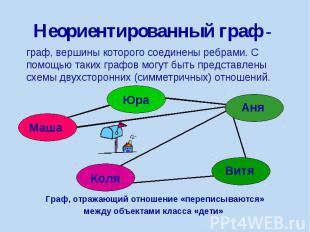
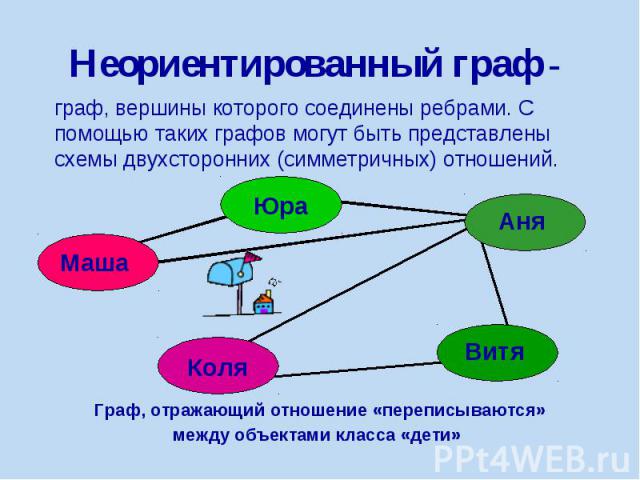
Неориентированный граф - граф, вершины которого соединены ребрами. С помощью таких графов могут быть представлены схемы двухсторонних (симметричных) отношений.

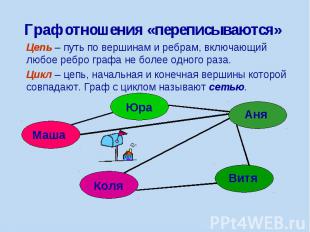
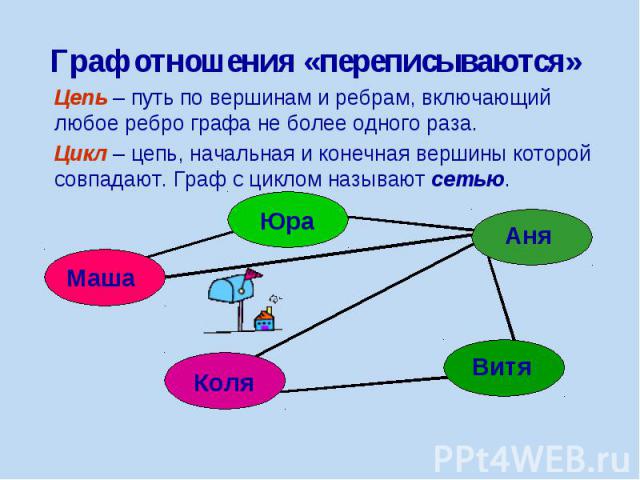
Граф отношения «переписываются» Цепь – путь по вершинам и ребрам, включающий любое ребро графа не более одного раза. Цикл – цепь, начальная и конечная вершины которой совпадают. Граф с циклом называют сетью.

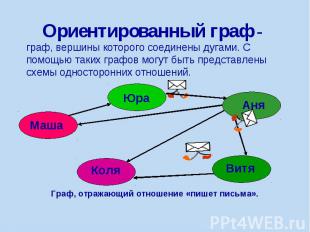
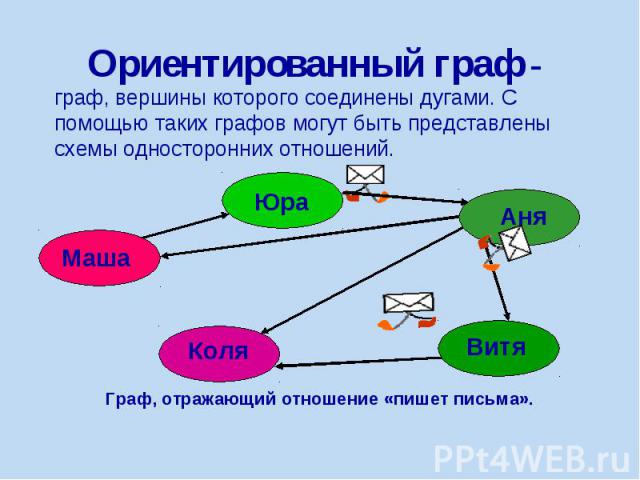
Ориентированный граф - граф, вершины которого соединены дугами. С помощью таких графов могут быть представлены схемы односторонних отношений.

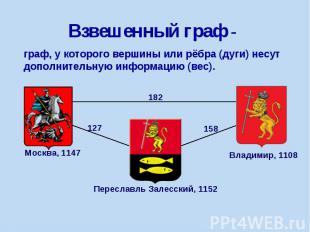
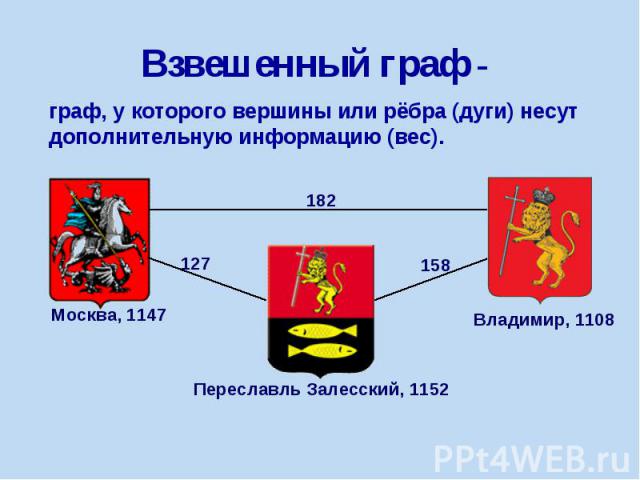
граф, у которого вершины или рёбра (дуги) несут дополнительную информацию (вес).

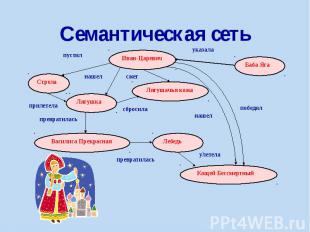
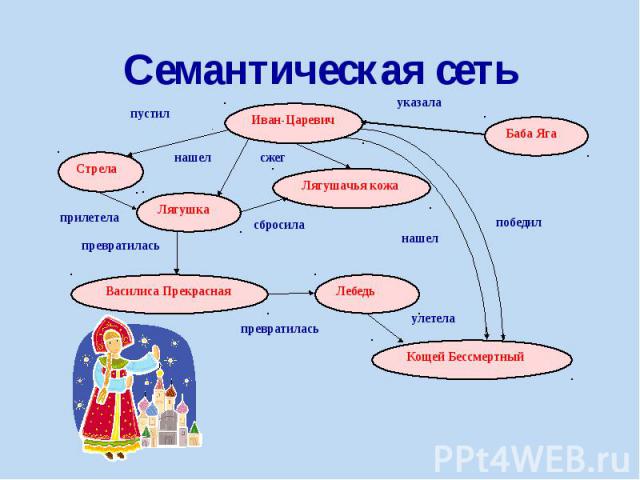
Семантическая сеть

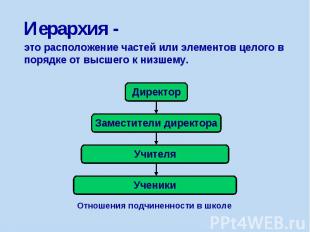
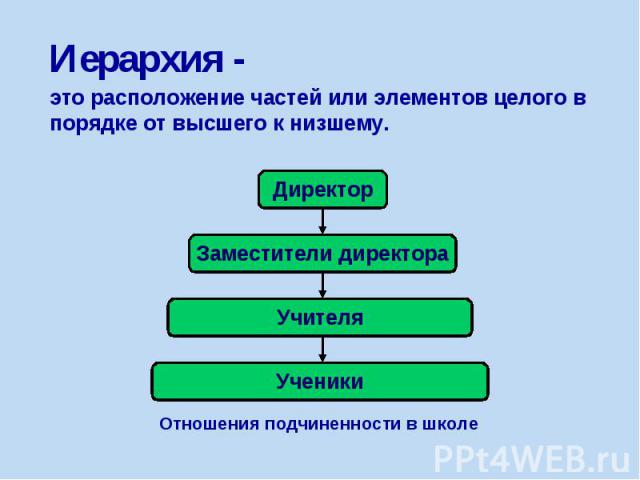
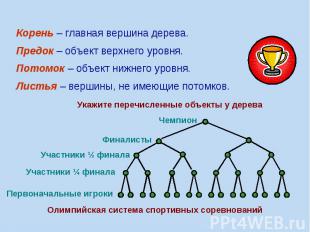
Иерархия -

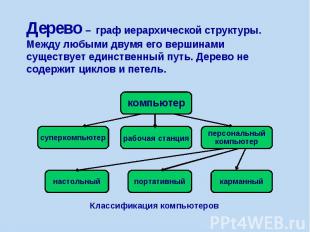
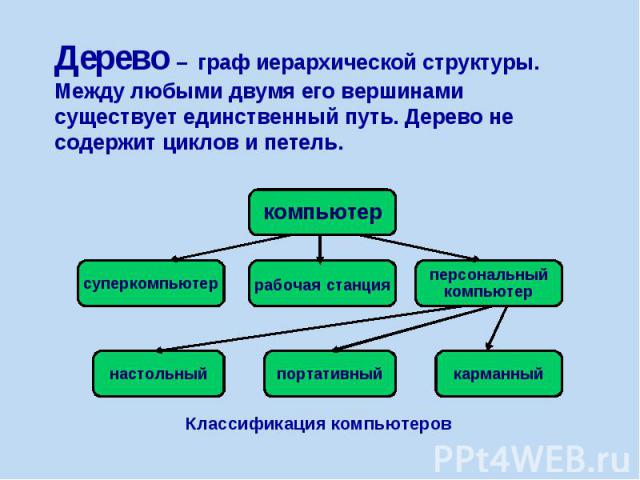
Дерево – граф иерархической структуры. Между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.

Файловая структура

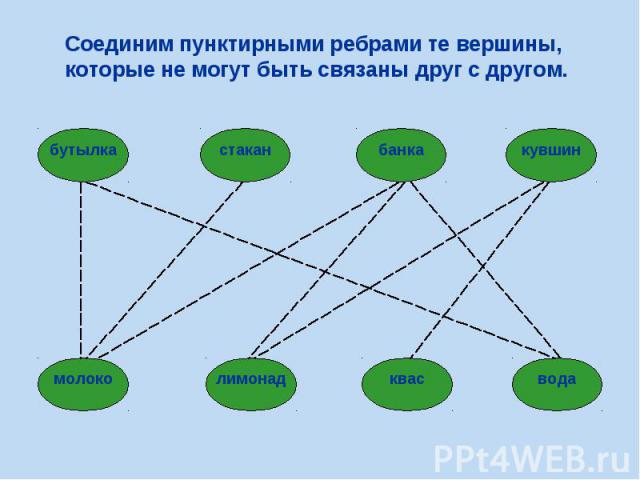
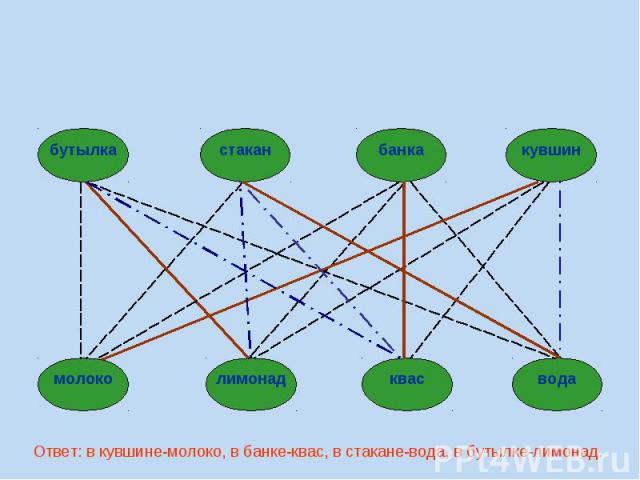
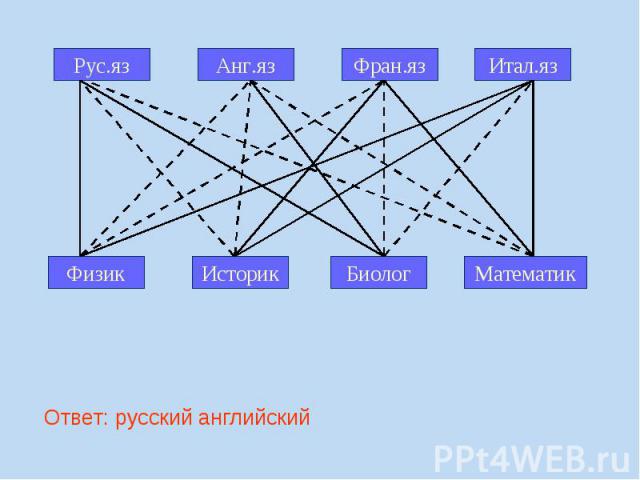
Задача:

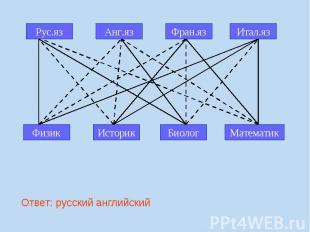
A10 (базовый уровень, время – 2 мин) Тема: Использование информационных моделей (таблицы, диаграммы, графики). Перебор вариантов, выбор лучшего по какому-то признаку. Что нужно знать: в принципе, особых дополнительных знаний, кроме здравого смысла и умения перебирать варианты (не пропустив ни одного!) здесь, как правило, не требуется полезно знать, что такое граф (это набор вершин и соединяющих их ребер) и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки

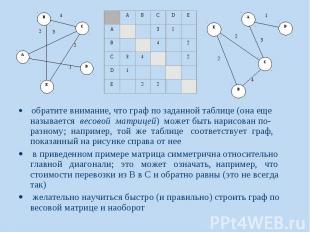
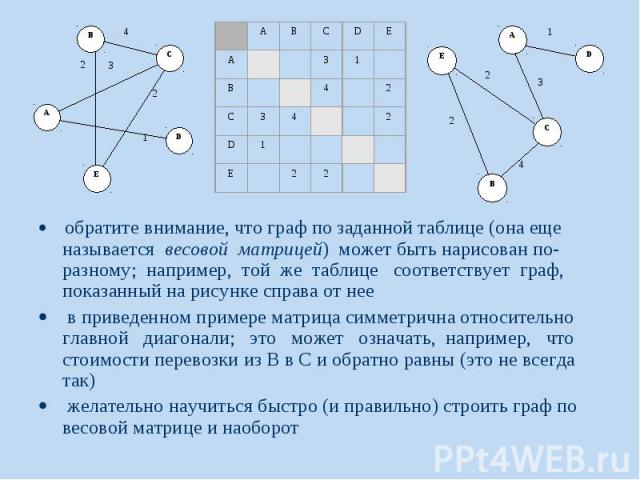
    обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее     обратите внимание, что граф по заданной таблице (она еще называется весовой матрицей) может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее     в приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так)     желательно научиться быстро (и правильно) строить граф по весовой матрице и наоборот

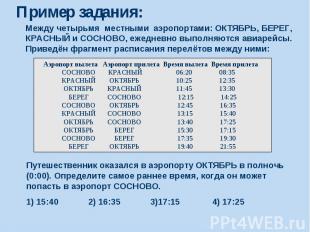
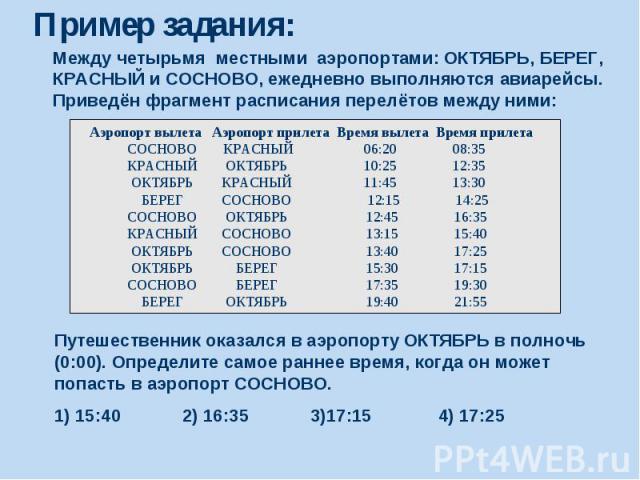
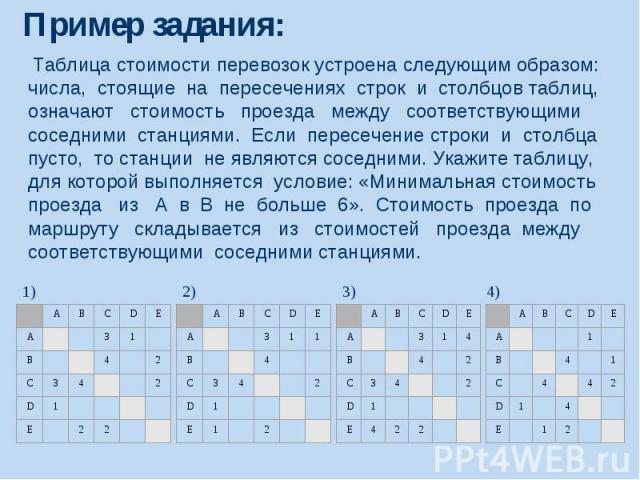
Пример задания:

Решение: 1)  есть прямой рейс из аэропорта ОКТЯБРЬ в СОСНОВО с прибытием в 17:25: ОКТЯБРЬ СОСНОВО 13:40 17:25 2)  сможет ли путешественник оказаться в СОСНОВО раньше этого времени, если полетит через другой аэропорт, с пересадкой 3)   можно лететь, через КРАСНЫЙ, но, как следует из расписания, ОКТЯБРЬ КРАСНЫЙ 11:45 13:30 … КРАСНЫЙ СОСНОВО 13:15 15:40 путешественник не успеет на рейс КРАСНЫЙ – СОСНОВО, который улетает в 13:15 4)   можно лететь через БЕРЕГ, БЕРЕГ СОСНОВО 12:15 14:25 … ОКТЯБРЬ БЕРЕГ 15:30 17:15 но рейс БЕРЕГ – СОСНОВО вылетает даже раньше, чем рейс ОКТЯБРЬ – БЕРЕГ 5)  правильный ответ – 4 (прямой рейс).

Возможные ловушки и проблемы: можно не заметить, что путешественник не успеет на пересадку в КРАСНОМ (неверный ответ 15:40) можно перепутать аэропорты вылета и прилета (неверный ответ 16:35)

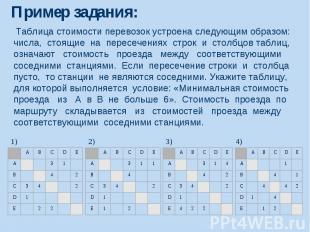
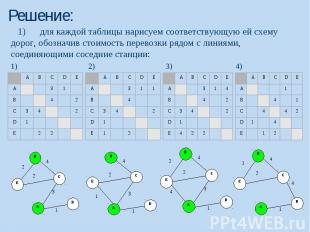
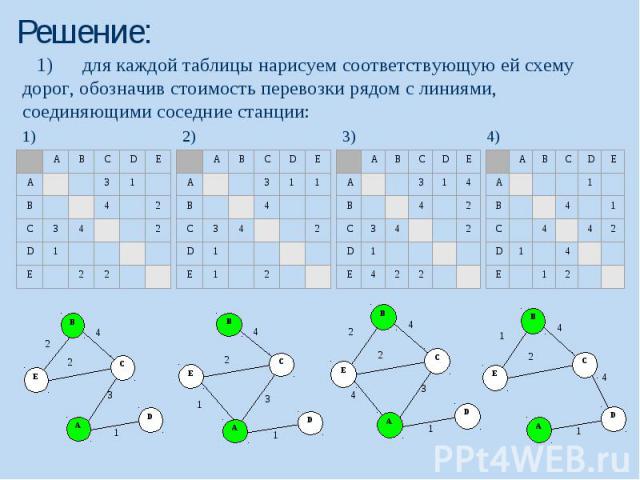
Решение:

Возможные ловушки и проблемы:

C3 (высокий уровень, время – 30 мин)

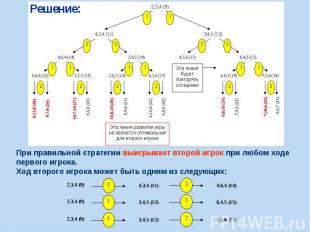
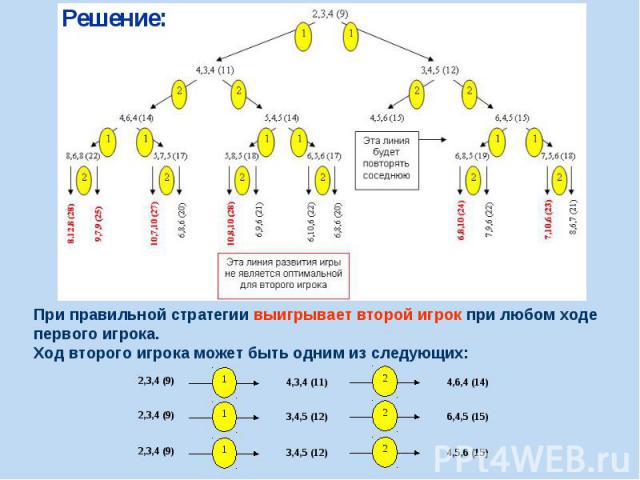
Решение:

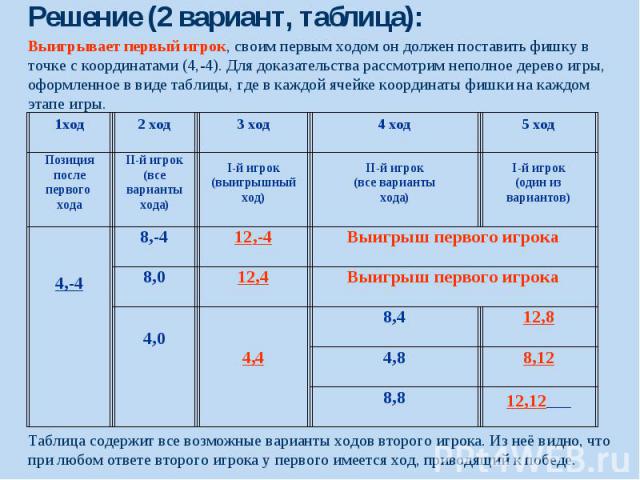
Решение (2 вариант, таблица):

Задача (ЕГЭ 2009г.):

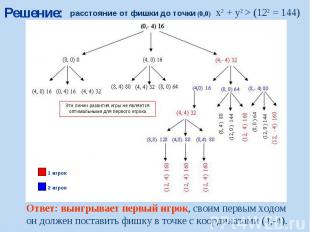
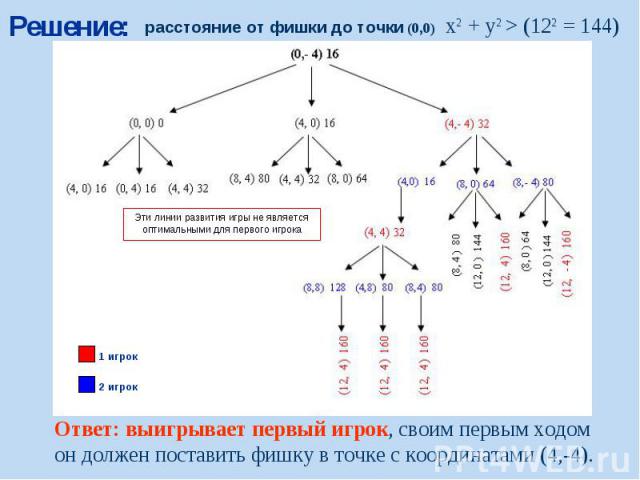
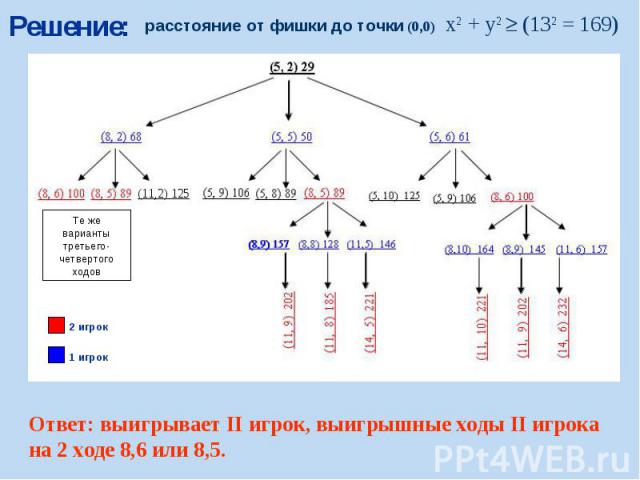
Решение:

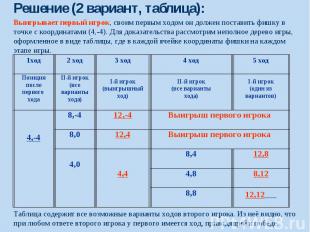
Решение (2 вариант, таблица):

Задача (ЕГЭ 2008г.):

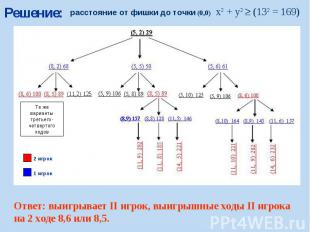
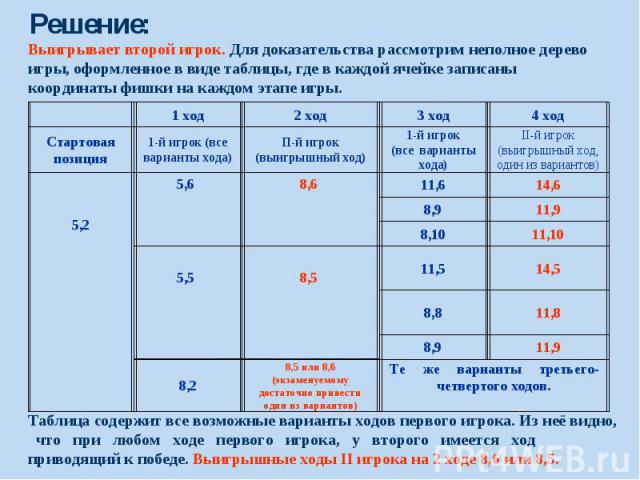
Решение:

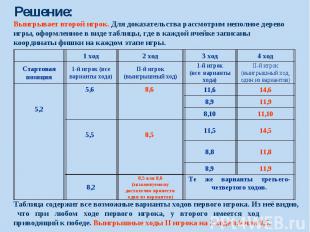
Решение:

Семенов А.Л., Рудченко Т.А. Информатика. 4 класс. Семенов А.Л., Рудченко Т.А. Информатика. 4 класс. Учебник. Рабочая тетрадь. Тетрадь проектов Л.Л. Босова. Информатика и ИКТ. Учебник для 7 класса. Рабочая тетрадь Тема: «Моделирование» в 11 классе. Семакин И. Задачник – практикум. 1 том

Приложение: