Презентация на тему: Решение текстовых задач «на работу»

Подготовка к ЕГЭ по математикеРешение текстовых задач «на работу»

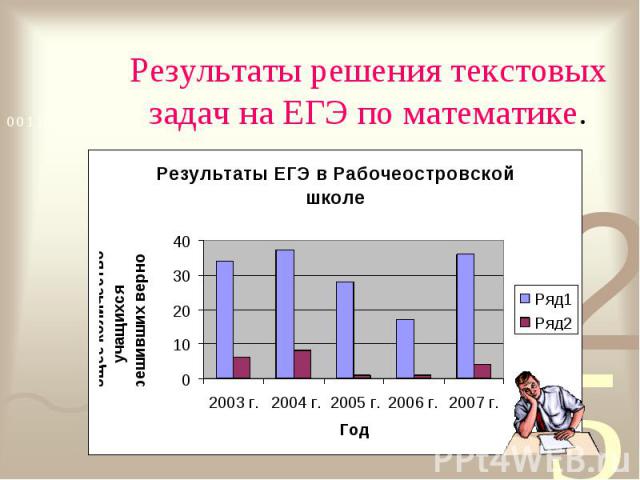
Результаты решения текстовых задач на ЕГЭ по математике.

Особенности решения задач «на работу». А=Р*t, где А-работа Р- производительность труда t- времяР=А/tt=А/РЕсли в условии не дана вся работа, то её можно принять за 1Общая производительность равна сумме производительностей.

Пример 1 Для наполнения плавательного бассейна водой имеются три насоса. Первому насосу для наполнения бассейна требуется времени в три раза меньше, чем второму, и на 2 ч больше, чем третьему. Три насоса, работая вместе, наполнили бы бассейн за 3ч, но по условиям эксплуатации одновременно должны работать только два насоса. Определите минимальную стоимость наполнения бассейна, если 1ч работы любого из насосов стоит 140 рублей. Решение: Эту задачу удобно решать с помощью таблицы.

Алгоритм решения задачи 1. Внесем в таблицу известные величины ( работу примем за 1) 2. Одну из неизвестных величин обозначим за х. 3. Остальные неизвестные величины выразим через х, используя условие задачи или формулы.. 4Составим уравнение. 5. Решим уравнение и ответим на главный вопрос задачи.

Уравнение 1/х+2 + 1/3(х+2) + 1/х = 1/3Решив уравнение, мы найдем х=66ч- время наполнения бассейна третьим насосом.Тогда время первого насоса 8ч, второго 24ч.Значит минимальное время работы двух насосов – это время работы 1 и3 насосов ,т.е. 14чОпределим минимальную стоимость наполнения бассейна двумя насосами.140*14=1960(руб.) Ответ: 1960 руб.

Реши сам! Два маляра, работая вместе, могут за 1ч покрасить стену площадью 40 кв.м. Первый маляр, работая отдельно, может покрасить 50 кв. м стены на 4ч быстрее, чем второй покрасит 90 кв.м такой же стены. За сколько часов первый маляр сможет покрасит 100 кв. м стены?Ответ: 4ч

Пример 2

Пример 3 Бак заполняют керосином за 2часа 30 минут с помощью трех насосов, работающих вместе. Производительности насосов относятся как 3:5:8. Сколько процентов объёма будет заполнено за 1час 18 минут совместной работы второго и третьего насосов?

Решение задачи Так как объём бака не указан, то примем объём бака за 1. Пусть коэффициент пропорциональности равен х, тогда производительности насосов соответственно равны 3х, 5х, 8х. И время наполнения бака при совместной работе всех трех насосов равно 1/3х+5х+8х = 1/ 16х или, по условию задачи, 2ч 30 мин. Решим уравнение 1/16х = 2,5Х =1/ 40Производительность второго насоса равна 1/ 40 * 5 = 1/ 8Производительность третьего насоса равна 1/ 40 * 8 = 1/ 5.Совместная производительность второго и третьего насосов равна 1/ 8 + 1/ 5 =13/40За 1ч 30мин второй и третий насосы наполнят 13/ 40 * 78/ 60 = 13/ 40 * 1,3 = 16,9/ 40 = 0,4225 объёма бака. Итак, при совместной работе 2 и 3 насосов за 1ч 18 мин будет заполнено 0,4225 *100% =42,25% объёма бака.

Реши сам ! Два фермера, работая вместе могут вспахать поле за 25 ч. Производительности труда первого и второго фермеров относятся как 2:5. Фермеры планируют работать поочередно. Сколько времени должен проработать второй фермер, чтобы это поле было вспахано за 45,5 ч?Ответ: 28 ч.