Презентация на тему: решение неравенств

Системы неравенств X2+13 14X X2+45 18X

Что это такое? Несколько неравенств с одной переменной х образуют систему неравенств, если ставится задача найти все такие значения переменной, при которых каждое из данных неравенств с переменной обращается в верное числовое неравенство. Любое такое значение х называют решением (или частным решением) системы неравенств.

Решение системы неравенств Рассмотрим систему неравенств 2х -1 3, 3х-2 11.

Можно подобрать несколько её частных решений, например х=3, х=4, х=3,2. В самом деле, при х=3 первое неравенство принимает вид 5 3, а второе – 7 11.Получилось два верных числовых неравенства, т.е. х=3 – частное решение данной системы. В то же время х=5 – не является частным решением, т.к первое неравенство принимает вид 9 3,т.е. вид верного числового неравенства, а второе – 13 11, это неверное числовое неравенство.

Решить систему неравенств – значит найти все ее частные решения. f(x) 0 g(x) 0 Пусть х1 – решение первого неравенства, а х2 – второго. Нас интересуют только те значения х, которые принадлежат и множеству х1 , и множеству х2. Значит нас интересует множество х1 х2 – это пересечение и является решением заданной системы неравенств.

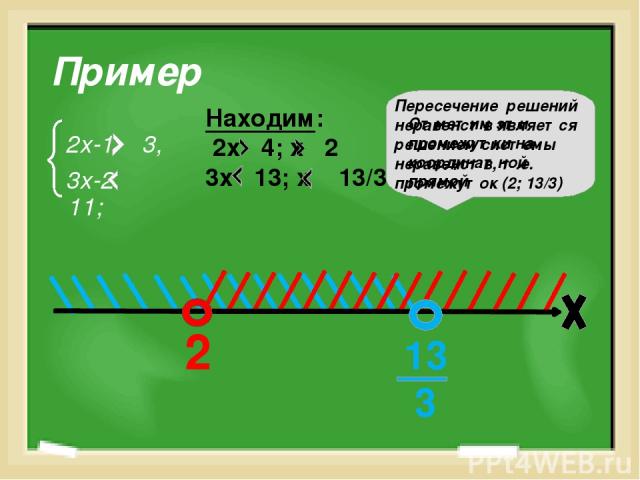
Пример 2х-1 3, 3х-2 11; Находим: 2х 4; х 2 3х 13; х 13/3 Отметим эти промежутки на координатной прямой 2 13 3 Пересечение решений неравенств является решением системы неравенств, т.е. промежуток (2; 13/3)

Вывод: Чтобы решить любую систему неравенств, нужно для каждого из неравенств найти множества значений х, при которых данное неравенство выполняется, а затем найти пересечение этих множеств, и это и будет являться ответом. Решением может являться как промежуток так и число и т.п.