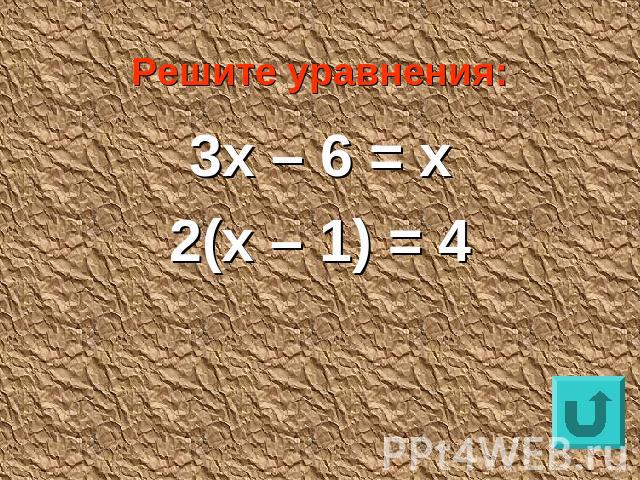Презентация на тему: Рациональные числа

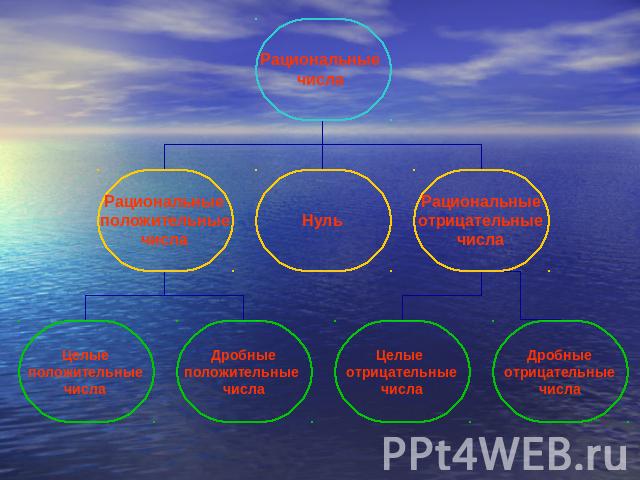
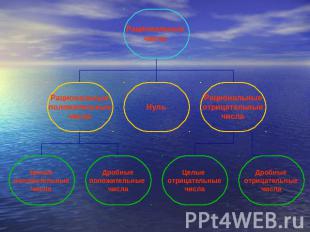
Рациональные числа

Проверка теоретических знаний.Устные упражнения.Историческая страничка. Отрицательные числа.Практические упражнения.Конкурс художников.Историческая страничка. Уравнения.Решение задач.Самостоятельная работа.

Проверка теоретических знаний

Ответьте на вопросы:Где на координатной прямой располагаются отрицательные числа и где положительные?Какие два числа называются противоположными? Какое число противоположно самому себе?Что называется модулем числа?Как сравнить два отрицательных числа?

Ответьте на вопросы:Как сравнить два числа с разными знаками?Сколькими числами определяется положение точки на: координатной плоскости? на координатной прямой? Как называются эти числа?Чему равна сумма противоположных чисел?

Ответьте на вопросы:Сформулируйте правило сложения двух отрицательных чисел.Сформулируйте правило сложения двух чисел с разными знаками.Сформулируйте правило раскрытия скобок, перед которыми стоит знак «+».

Ответьте на вопросы:Сформулируйте правило раскрытия скобок, перед которыми стоит знак «-».Сформулируйте правило умножения двух отрицательных чисел.Сформулируйте правило умножения двух чисел с разными знаками.

Ответьте на вопросы:Сформулируйте правило деления двух отрицательных чисел.Какие слагаемые называются подобными?Сформулируйте правило приведения подобных слагаемых.

Устные упражнения

Найдите значение выражения:- 56 + 67; - 19,1 – 13,1; - 0,2 ∙ 4; - 8 ∙ (- 0,125)

Найдите значение выражения:100 : (- 2,5); 20 : (- 0,1); (- 7 – 3) ∙ (- 16 : 4)

Упростите выражение:- (3а – 7)5 + (3 – 2х)

Сравните:

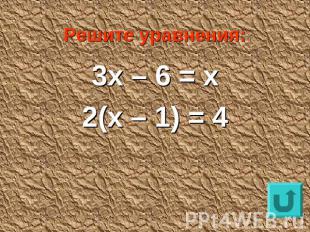
Решите уравнения:3х – 6 = х2(х – 1) = 4

Историческая страничка

Когда и где появились отрицательные числа? Ни египтяне, ни вавилоняне, ни даже древние греки чисел этих не знали. Впервые с отрицательными числами столкнулись китайские учёные (II в. до н. э.) в связи с решением уравнений.

Однако знаки «+» или «-» тогда не употребляли, а изображали положительные числа красным цветом, а отрицательные – чёрным, называя их «фу».

Индийские математики Брахмагупта (VII в.) и Бхаскара (XII в.) с помощью положительных чисел выражали «имущество», а с помощью отрицательных – «долг». Они составили правила действий для этих чисел.

Однако долгое время отрицательные числа считали ненастоящими, фиктивными, абсурдными. Даже Бхаскара, который пользовался этими числами, писал: «Люди не одобряют отрицательные числа».

В Европе к отрицательным числам в XIII в. обращается итальянский математик Леонардо Фибоначчи, но в учении об отрицательных числах значительно далее продвинулся М. Штифель (XVI в.)

Отрицательные числа он называл как «меньше, чем ничто» и говорил, что «нуль находится между истинными и абсурдными числами». И только после работ выдающегося учёного Р. Декарта (XVII в.) и других учёных XVII-XVIII в. отрицательные числа приобрели «права гражданства».

Практические упражнения

Расположите результаты в порядке убывания:- 0,8 ∙ (1,7 – 5,1) – 6,3 : (- 0,9) + 1,1 Р3,5 ∙ (- 5,6 + 4,9) + 7,2 : (- 0,8) - 5,4 О- 1,4 ∙ (3,1 – 7,2) – 0,64 : (- 1,6) + 1,5 Е4,1 ∙ (- 9,2 + 7,9) + 0,16 : (- 0,2) – 6,1 З- 1,1 ∙ (- 6,9 – 2,1) – 1,21 : (- 11) + 3,2 Т7,3 ∙ (- 4,2 – 3,9) + 0,81 : (- 0,03) – 7,9 К- 2,5 ∙ (- 4 – 8,4) – 14,4 : (- 1,2) + 1,8 О

Конкурс художников

О чём мечтают большинство мальчишек в детстве? A (0; 9) B(2; 6) C (2; - 3) D (3; - 5) E (3; - 10) F (2; - 8) K(- 2; - 8) M (- 3; - 10) N (- 3; - 5) O (- 2; - 3) P (- 2; 6) A (0; 9).R (- 1; 5) S (1; 5) Т (1; 3) Z (- 1; 3) R (- 1; 5).Q (- 1; 1) Х (1; 1) Y (1; - 1) Z (- 1; - 1) Q ( - 1; 1).

Красивая птица, живущая в Африке, которая не умеет летать.A(2; - 8) B(1; - 7) C(2; 0) D(4;5) E(4; 9) F(6; 10) K(2; 11) M(2; 5) N(0; 8) Y(- 4; 6) P(- 3; 3) R(- 2; 3) Q(- 3; 1) X(- 1; 1) O(0; 0) Z(0; - 8) A(2; - 8).

Историческая страничка

Когда и какие народы начали первыми использовать уравнения? Ещё 3-4 тыс. лет до н. э. египтяне и вавилоняне, пользуясь таблицами и готовыми разработанными рецептами, умели решать некоторые уравнения.

Разумеется, приёмы решения у них были вовсе не такие, как теперь. Греки, унаследовавшие математические знания египтян и вавилонян, пошли дальше.

Наибольших успехов в решении уравнений добился греческий учёный Диофант (III в).О нём писали:Посредством управлений, теорем Он уйму всяких разрешил проблем: И засуху предсказывал, и ливни -Поистине его познанья дивны.

Стройное учение об уравнениях разработал среднеазиатский учёный Мухамед-аль-Хорезми (IX в.). В дальнейшем проблема решений уравнений занимала умы всех математиков.

Решение задач

- Скажите мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?- Вот сколько,- ответил Пифагор,- половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении и, кроме того, есть ещё три женщины.

Летела стая гусей, а навстречу им гусь. - Здравствуйте, сто гусей – говорит он им. - Нас не сто, - отвечают они ему. - Вот если бы нас было столько, сколько есть, да еще раз столько, да полстолько, да четверть столько, да ты с нами, тогда было бы сто. Сколько было гусей в стае?

В школе №1 обучается учащихся в два раза больше, чем в школе №18. Если после заселения нового микрорайона из школы №1 перейдёт по месту нового жительства 411 учеников в школу №18, то в обеих школах учащихся будет поровну. Сколько учащихся в данный момент обучается в каждой из школ?

Самостоятельная работа

Решите уравнения:а) 3(x – 5) = -(-x – 3); б) 9(x – 3) = 5(x + 5); в) -6a + 16 = 4a – 6a – 24; г) 2x + 3 = 7; д) 3x – 7 = 5x – 9; е) 2(x – 1) = 3x – 1.

Найдите ошибку:а) 2x + 15 = 7, 2x = 15 – 7, 2x = 8, x = 4.

Найдите ошибку:в) 6 – 12a = 4, - 12a = - 6 + 4, - 12a = - 2, a = 6.