Презентация на тему: Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач

ОРГАНИЗАЦИЯ ПОИСКОВОЙ И РЕФЛЕКСИВНОЙДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ ПРИ РЕШЕНИИПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ Директор гимназии № 3, Заслуженный учитель России Т.Ю.Пупанова,доктор педагогических наук. заведующий кафедрой МОМ и ИТ И.Е. Малова,Брянск, 2010

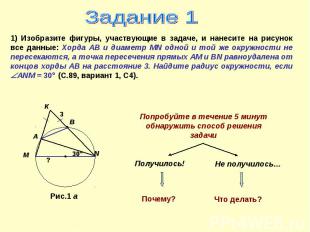
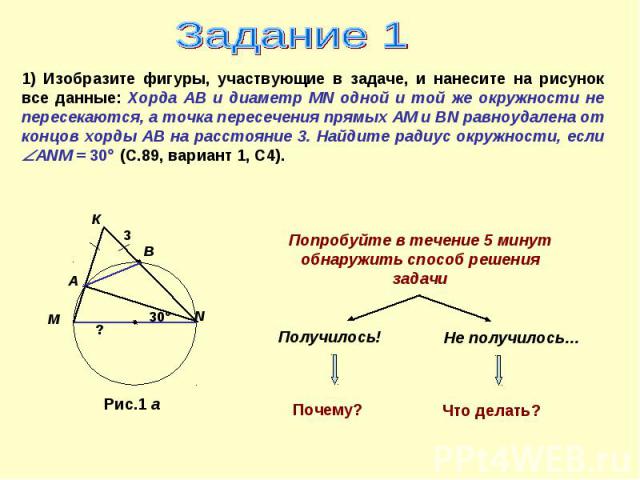
Задание 1 1) Изобразите фигуры, участвующие в задаче, и нанесите на рисунок все данные: Хорда АВ и диаметр MN одной и той же окружности не пересекаются, а точка пересечения прямых АМ и ВN равноудалена от концов хорды АВ на расстояние 3. Найдите радиус окружности, если АNМ = 30 (С.89, вариант 1, С4). Попробуйте в течение 5 минут обнаружить способ решения задачи

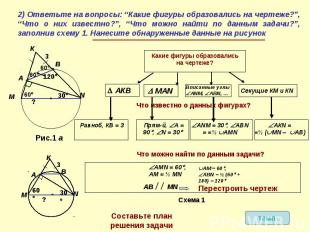
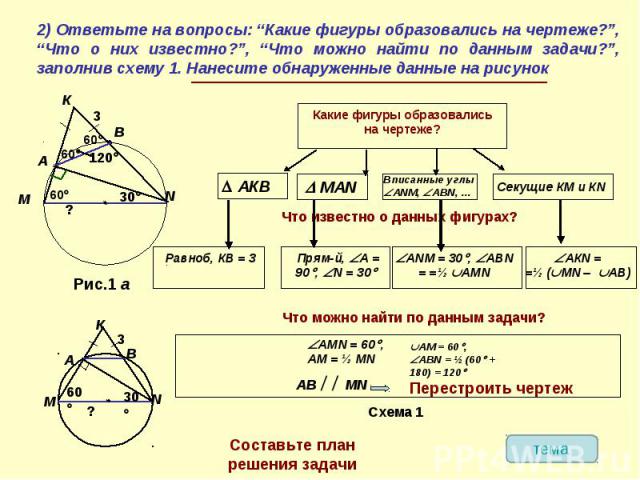
2) Ответьте на вопросы: “Какие фигуры образовались на чертеже?”, “Что о них известно?”, “Что можно найти по данным задачи?”, заполнив схему 1. Нанесите обнаруженные данные на рисунок

Рассмотрите еще один способ доказательства того, что треугольник МКN – равносторонний.В МКN проведена высота NА. Из соображений симметрии, выполним дополнительное построение, соединив точки М и В.Аналогично тому, что NА высота, можно доказать, что МВ – высота МКN. Из планиметрии известно, что треугольник, образованный основаниями двух высот остроугольного треугольника и его вершиной, подобен данному. Значит, МКN подобен АКВ. По условию АКВ равнобедренный, значит, МКN – равнобедренный. Но в МКN угол АМN = 600, значит, МКN – равносторонний.

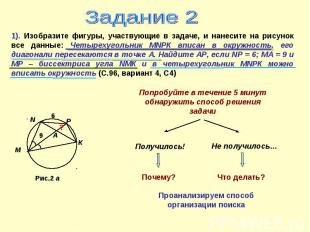
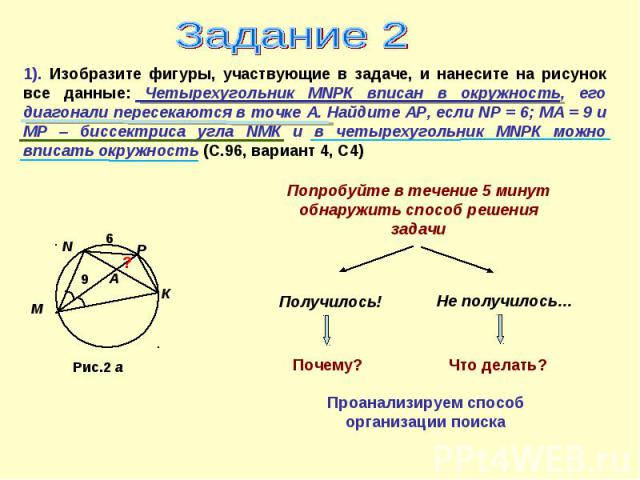
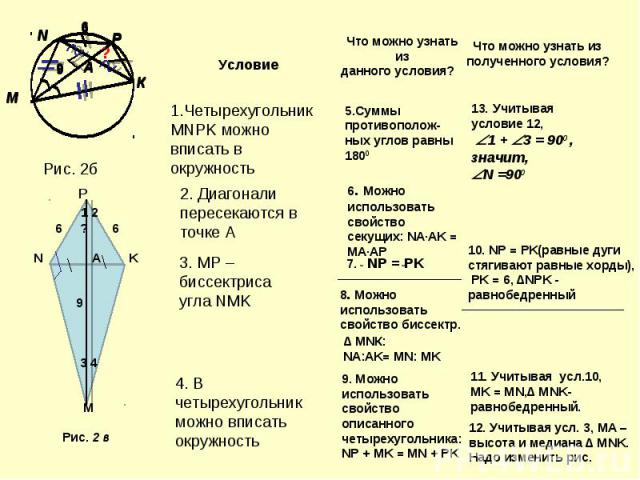
Задание 21). Изобразите фигуры, участвующие в задаче, и нанесите на рисунок все данные: Четырехугольник МNРК вписан в окружность, его диагонали пересекаются в точке А. Найдите АР, если NР = 6; МА = 9 и МР – биссектриса угла NМК и в четырехугольник МNРК можно вписать окружность (С.96, вариант 4, С4) Попробуйте в течение 5 минут обнаружить способ решения задачи

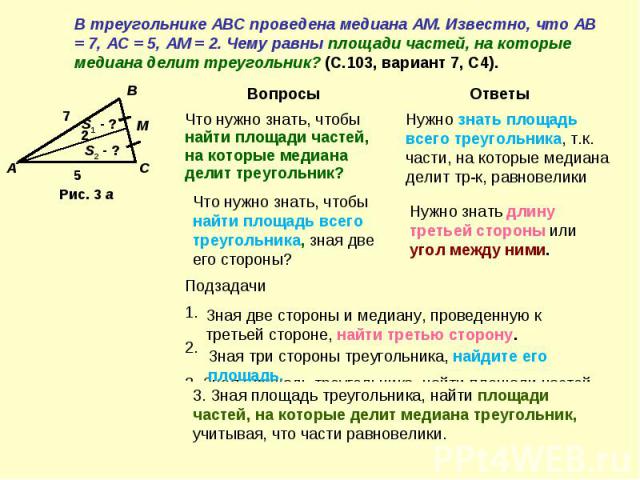
Задание 31). Изобразите фигуры, участвующие в задаче, и нанесите на рисунок все данные: В треугольнике АВС проведена медиана АМ. Известно, что АВ = 7, АС = 5, АМ = 2. Чему равны площади частей, на которые медиана делит треугольник? (С.103, вариант 7, С4). Попробуйте в течение 5 минут обнаружить способ решения задачи

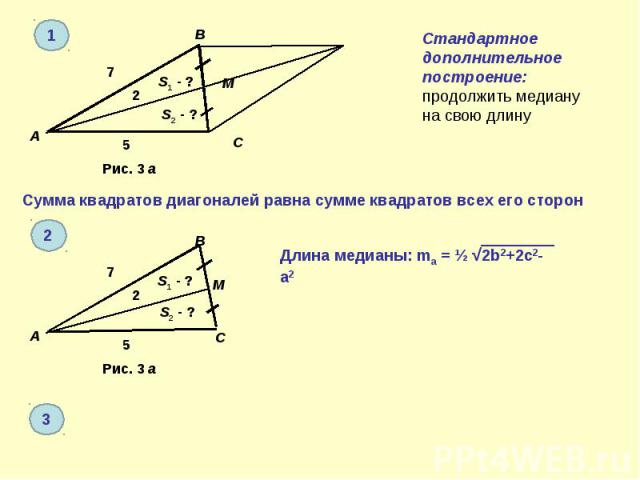
В треугольнике АВС проведена медиана АМ. Известно, что АВ = 7, АС = 5, АМ = 2. Чему равны площади частей, на которые медиана делит треугольник? (С.103, вариант 7, С4).

Стандартное дополнительное построение: продолжить медиану на свою длинуСумма квадратов диагоналей равна сумме квадратов всех его сторон

Задание 4 1). Прочитайте задачу: В треугольнике АВС высота СН и медиана СК делят угол АСВ на три равных угла. Длина отрезка СО, где О – центр вписанной окружности, равна . Найдите площадь треугольника АВС. (С.119, вариант 13, С4).Поскольку величина не является привычной, обозначьте ее какой-нибудь буквой и временно отбросьте. Изобразите фигуры, участвующие в задаче без этой величины, и нанесите на рисунок оставшиеся данные. Выясните свойства треугольника, у которого высота и медиана, проведенные из одной и той же вершины треугольника, делят его угол на три равные части ( №349, уч-к Л.С.Атанасян, 7 – 9 кл), отвечая на вопросы: “Какие фигуры образовались на чертеже?”, “Что о них известно?”, “Что можно узнать по данным задачи?”, “Что можно узнать по полученным условиям?”. (Вопросы и ответы занесите в таблицу).

В треугольнике АВС высота СН и медиана СК делят угол АСВ на три равных угла. Длина отрезка СО, где О – центр вписанной окружности, равна . Найдите площадь треугольника АВС.

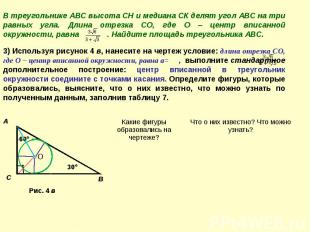
В треугольнике АВС высота СН и медиана СК делят угол АВС на три равных угла. Длина отрезка СО, где О – центр вписанной окружности, равна . Найдите площадь треугольника АВС. 3) Используя рисунок 4 в, нанесите на чертеж условие: длина отрезка СО, где О – центр вписанной окружности, равна а= , выполните стандартное дополнительное построение: центр вписанной в треугольник окружности соедините с точками касания. Определите фигуры, которые образовались, выясните, что о них известно, что можно узнать по полученным данным, заполнив таблицу 7.

Задачи про вневписанную окружность Учитель высшей категории СОШ №3 г. Стародуба И.А. Коваленко г.Стародуб2010

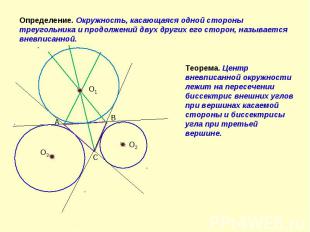
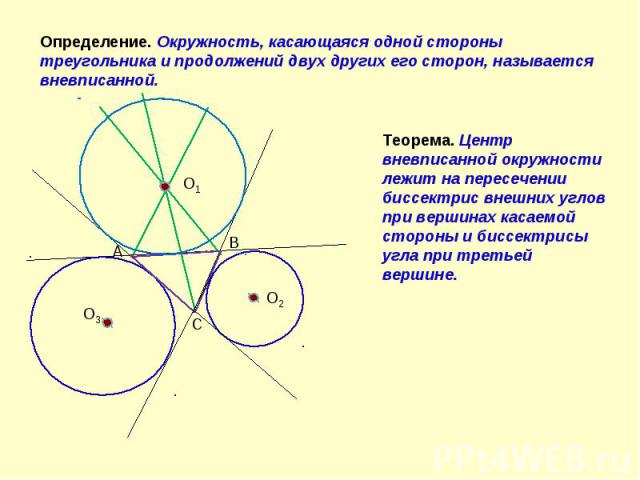
Определение. Окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон, называется вневписанной. Теорема. Центр вневписанной окружности лежит на пересечении биссектрис внешних углов при вершинах касаемой стороны и биссектрисы угла при третьей вершине.

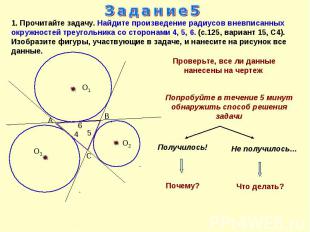
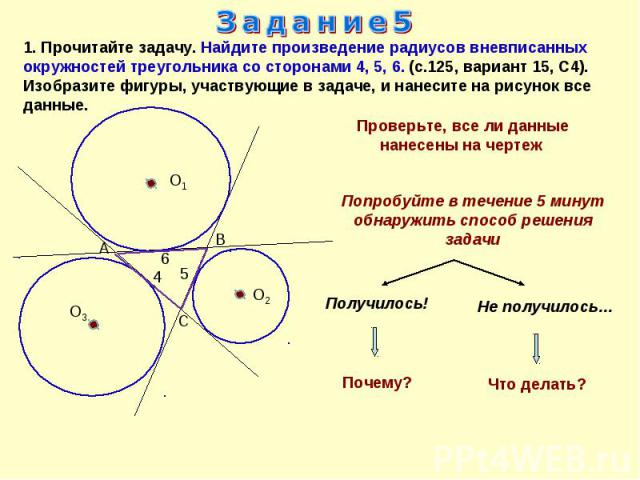
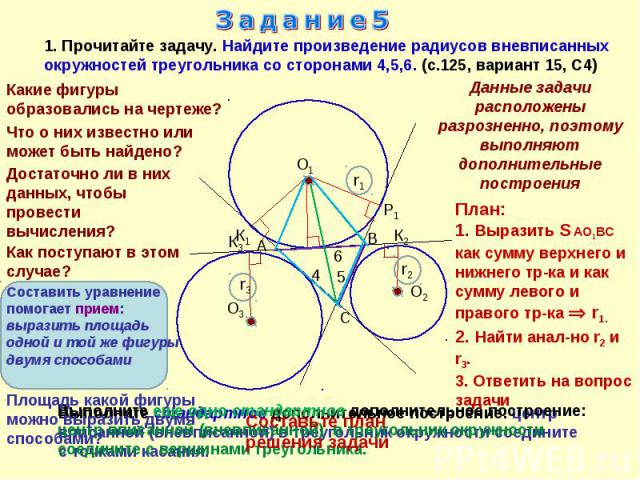
Задание5 1. Прочитайте задачу. Найдите произведение радиусов вневписанных окружностей треугольника со сторонами 4, 5, 6. (с.125, вариант 15, С4). Изобразите фигуры, участвующие в задаче, и нанесите на рисунок все данные.Проверьте, все ли данные нанесены на чертеж Попробуйте в течение 5 минут обнаружить способ решения задачи

Задание51. Прочитайте задачу. Найдите произведение радиусов вневписанных окружностей треугольника со сторонами 4,5,6. (с.125, вариант 15, С4)Какие фигуры образовались на чертеже?Что о них известно или может быть найдено? Достаточно ли в них данных, чтобы провести вычисления?Как поступают в этом случае?Составить уравнение помогает прием: выразить площадь одной и той же фигуры двумя способамиПлощадь какой фигуры можно выразить двумя способами?Данные задачи расположены разрозненно, поэтому выполняют дополнительные построенияПлан:1. Выразить S АО1ВС как сумму верхнего и нижнего тр-ка и как сумму левого и правого тр-ка r1.2. Найти анал-но r2 и r3.3. Ответить на вопрос задачи

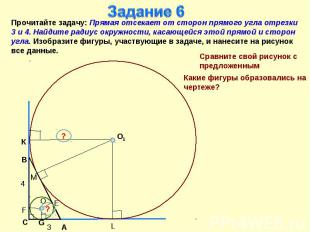
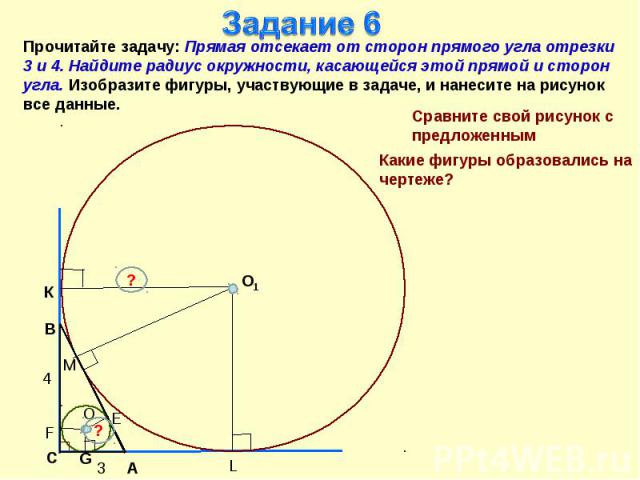
Задание 6Прочитайте задачу: Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите радиус окружности, касающейся этой прямой и сторон угла. Изобразите фигуры, участвующие в задаче, и нанесите на рисунок все данные.Сравните свой рисунок с предложеннымКакие фигуры образовались на чертеже?

План решения задачи1. Найти площадь и полупериметр тр-ка АВС ⇒ радиус вписанной окружности.2. Используя метод площадей, найти радиус вневписанной окружности.3. Ответить на вопрос задачи.