Презентация на тему: Кейс-технологии на уроках математики

Кейс-метод Кейс-метод реальный случай, который можно перевести из статуса «жизненной ситуации» в статус задачи, и затем решать с последующей рефлексией хода и ресурсов решения. Название метода происходит от англ.case – случай, ситуация и от понятия «кейс» - чемоданчик для хранения различных бумаг, документов, журналов и пр.

Одной из новых форм эффективных технологий обучения является проблемно-ситуативное обучение с использованием кейсов. Внедрение учебных кейсов в практику российского образования в настоящее время является весьма актуальной задачей. Кейс представляет собой описание конкретной реальной ситуации, подготовленное по определенному формату и предназначенное для обучения учащихся анализу разных видов информации, ее обобщению, навыкам формулирования проблемы и выработки возможных вариантов ее решения в соответствии с установленными критериями. Одной из новых форм эффективных технологий обучения является проблемно-ситуативное обучение с использованием кейсов. Внедрение учебных кейсов в практику российского образования в настоящее время является весьма актуальной задачей. Кейс представляет собой описание конкретной реальной ситуации, подготовленное по определенному формату и предназначенное для обучения учащихся анализу разных видов информации, ее обобщению, навыкам формулирования проблемы и выработки возможных вариантов ее решения в соответствии с установленными критериями. Кейсовая технология (метод) обучения – это обучение действием. Суть кейс–метода состоит в том, что усвоение знаний и формирование умений есть результат активной самостоятельной деятельности учащихся по разрешению противоречий, в результате чего и происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.

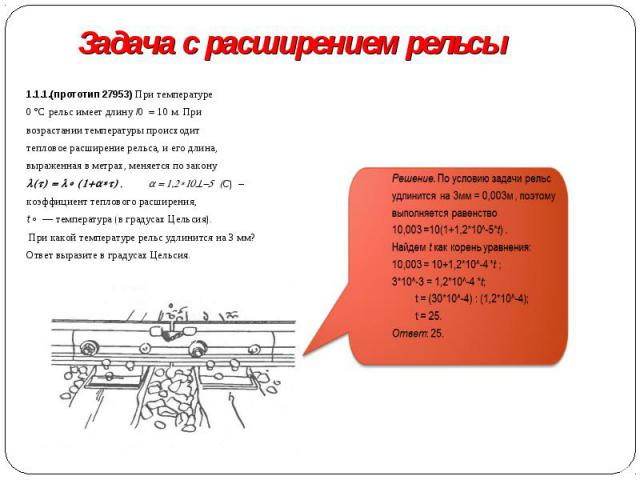
1.1.1.(прототип 27953) При температуре 1.1.1.(прототип 27953) При температуре 0 °C рельс имеет длину l0 = 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(t) = lo (1+a*t) , где a = 1,2*10^-5 (C) – коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

5.3.1.(прототип 27958) Если достаточно быстро вращать ведерко с водой на веревке в вертикальной плоскости, то вода не будет выливаться. При вращении ведерка сила давления воды на дно не остается постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила ее давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P = m( u^2 : L – g) , где m – масса воды в килограммах, u — скорость движения ведерка в м/с, L – длина веревки в метрах, g – ускорение cвободного падения (считайте g = 10 м / с2 ). С какой наименьшей скоростью надо вращать ведерко, чтобы вода не выливалась, если длина веревки 5.3.1.(прототип 27958) Если достаточно быстро вращать ведерко с водой на веревке в вертикальной плоскости, то вода не будет выливаться. При вращении ведерка сила давления воды на дно не остается постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила ее давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна P = m( u^2 : L – g) , где m – масса воды в килограммах, u — скорость движения ведерка в м/с, L – длина веревки в метрах, g – ускорение cвободного падения (считайте g = 10 м / с2 ). С какой наименьшей скоростью надо вращать ведерко, чтобы вода не выливалась, если длина веревки равна 40 см? Ответ выразите в м/с.

7.2.1.(прототип 27971) Перед отправкой тепловоз издал гудок с частотой f0 = 400 Гц. 7.2.1.(прототип 27971) Перед отправкой тепловоз издал гудок с частотой f0 = 400 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону f(u) = fo : (1 - u:c) (Гц) где c – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Опреде- лите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а c = 315 м/с. Ответ выразите в м/с.

7.1.1.(прототип 27970) Для получения на 7.1.1.(прототип 27970) Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана – в пределах от 150 до180 см. Изображение на экране будет четким, если выполнено соотношение (1 : d1 )+ (1 : d2) = 1 : f . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.

1) Прочитать задачу. 2) Прочитать внимательно, что нужно найти. 3) Подставить данные задачи в формулу и проанализировать. 4) Вычислить. 5) Записать ответ.

Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q (единиц в месяц) от её цены p (тыс. руб.) задаётся формулой q = 255 -15p. Определите максимальный уровень цены p (тыс. руб.) при котором значение выручки предприятия за месяц r = qp составит не менее 990 тыс. руб. Для одного из предприятий-монополистов зависимость объёма спроса на продукцию q (единиц в месяц) от её цены p (тыс. руб.) задаётся формулой q = 255 -15p. Определите максимальный уровень цены p (тыс. руб.) при котором значение выручки предприятия за месяц r = qp составит не менее 990 тыс. руб.

Определите максимальный уровень цены p (тыс. руб.) при котором значение выручки предприятия за месяц r = qp составит не менее 990 тыс. руб. Определите максимальный уровень цены p (тыс. руб.) при котором значение выручки предприятия за месяц r = qp составит не менее 990 тыс. руб.

q=255-15p, r =qp, r =(255-15p)p q=255-15p, r =qp, r =(255-15p)p По условию задачи p не должно быть меньше 990. Составим неравенство: 255p-15 p 2 = 990

Решим квадратное неравенство: p принадлежит отрезку [6;11] ; выберем наибольший корень p=11. Решим квадратное неравенство: p принадлежит отрезку [6;11] ; выберем наибольший корень p=11. Значит максимальный уровень цены равен 11 тыс. руб. 4) Запишем ответ. Ответ: p=11.

1)Внимательно прочитать условие задачи. 2)Выписать все данные для каждого случая. 3)Посчитать. 4)Выбрать оптимальный из 2 (3) вариантов 5)Записать готовый ответ в требуемых единицах измерения.

 В таблице даны тарифы на услуги трех фирм такси.  В таблице даны тарифы на услуги трех фирм такси. Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки. Нужно выбрать фирму, в которой поездка длительностью 60 минут будет стоить дешевле всего. Сколько рублей будет стоить этот заказ? 3) Первая фирма – 920 руб. Вторая фирма – 1100 руб. Третья фирма – 1095 руб. 4) Оптимальный вариант – стоимость проезда у первой фирмы. 5) Ответ: 920 руб.

    Интернет провайдер-I   Интернет-провайдер-I (компания, оказывающая услуги по подключению к сети Интернет) предлагает тарифный План"0". Абонентская плата 0,00руб. Плата за 1 Мb трафика составляет 2,5 руб.     Интернет провайдер-II   Интернет-провайдер-II (компания, оказывающая услуги по подключению к сети Интернет) предлагает тарифный План"500". Абонентская плата 850 р. за 500 Мb трафика в месяц. Плата за 1 Мb трафика составляет 2 руб сверх 500 Мb.      Интернет провайдер-III   Интернет-провайдер-III (компания, оказывающая услуги по подключению к сети Интернет) предлагает тарифный План"800". Абонентская плата 1100 р. за 800 Мb трафика в месяц. Плата за 1 Мb трафика составляет 1,5 руб сверх 800 Мb