Презентация на тему: ШАГ ЗА ШАГОМ №1 к ОГЭ 2014

1.6.68. Решить уравнение 3х³-5х²-х-2=0 Решение. Корни кубического уравнения 3х³-5х²-х-2=0 находятся среди делителей свободного члена -2. А это числа: -2; -1; 1; 2. Проверим эти числа: -2: -24-20+2-2 ≠ 0 => -1: -3-5+1-2 ≠ 0 => 1: 3-5-1-2 ≠ 0 => 2: 24-20-2-2 = 0 => корень

1.6.67. Решить уравнение 4х³+х²-3х=2 Решение. Корни кубического уравнения 4х³+х²-3х-2=0 находятся среди делителей свободного члена -2. А это числа: -2;-1;1;2. Проверим каждое число: -2: -32 +4+6-2 ≠ 0 => не корень -1: -4+1+3-2 ≠ 0 => не корень 1: 4+1-3-2 = 0 => корень 2: 32 +4 -6-2 ≠ 0 => не корень

2-ой способ решения уравнения 4х³+х²-3х=2 4х³+х²-3х-2=0 Разложим левую часть уравнения на множители (4х³+х²)-(3х+2)=0 (4х³+х²)-(3х+2-х+х)=0 (4х³+х²)-(4х+1-х+1)=0 х²(4х+1)-(4х+1)+х-1=0 (х²(4х+1)-(4х+1)) +(х-1)=0

продолжение (х²(4х+1) - (4х+1))+(х-1)=0 (4х+1)(х²-1)+(х-1)=0 (4х+1)(х-1)(х+1)+(х-1) =0 (х-1)((4х+1)(х+1) +1)=0 (х-1)(4х²+4х+х+1 +1)=0 (х-1)(4х²+5х+2)=0, произведение равно нулю, значит х-1=0 или 4х²+5х+2=0 х=1 или D=25 -4·4·2<0 => нет корней. Ответ:1

1.6.70. Решите неравенство - 3х³ +7х +2х² +2 <0 Решение. Решим соответствующее уравнение - 3х³ +7х +2х² +2 =0. Разложим левую часть уравнения на множители способом группировки (- 3х³ +2х²) + (7х +2)=0 -х²(3х-2)+(3х-2 +2 +4х+2)=0 -х²(3х-2)+(3х-2) +2+4х+2=0 (-х²(3х-2)+(3х-2)) +(4х+4)=0 (-х²(3х-2)+(3х-2)) +4(х+1)=0

продолжение ((3х-2)(-х²+1)) +4(х+1)=0 ((3х-2) (1- х²)) +4(х+1)=0 ((3х-2) (1- х)(1+х)) +4(1+х) =0 (1+х)((3х-2)(1- х)+4)=0 (1+х)(3х-3х²-2+2х +4)=0 (1+х)(-3х²+5х+2)=0, тогда 1+х=0 или -3х²+5х+2=0 х=-1 или D=25- 4·(-3)·2=49 => х1=(5+7):6=2 и х2=(5-7):6=- 1/3

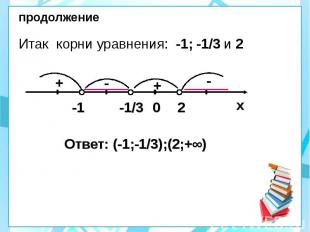
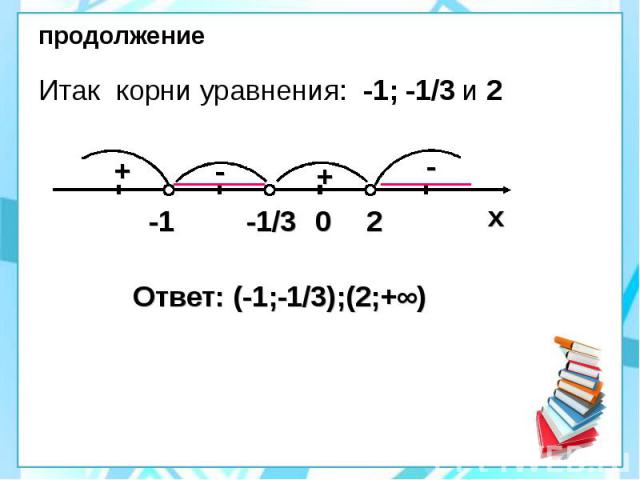
продолжение Итак корни уравнения: -1; -1/3 и 2 Ответ: (-1;-1/3);(2;+∞)

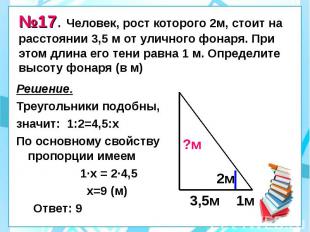
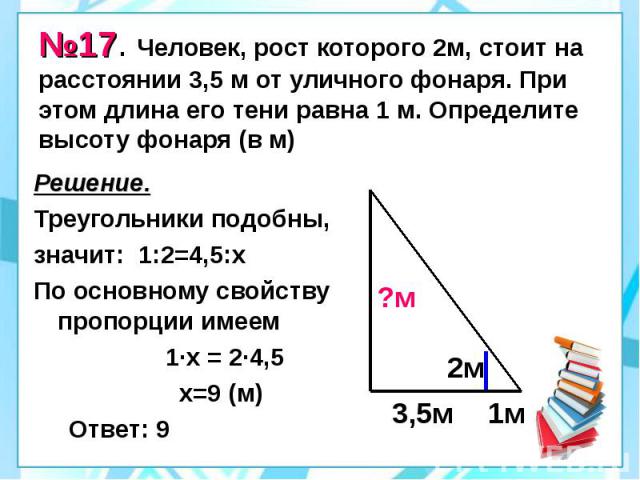
№17. Человек, рост которого 2м, стоит на расстоянии 3,5 м от уличного фонаря. При этом длина его тени равна 1 м. Определите высоту фонаря (в м) Решение. Треугольники подобны, значит: 1:2=4,5:х По основному свойству пропорции имеем 1·х = 2·4,5 х=9 (м) Ответ: 9

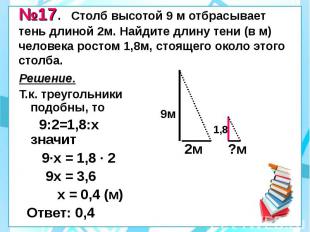
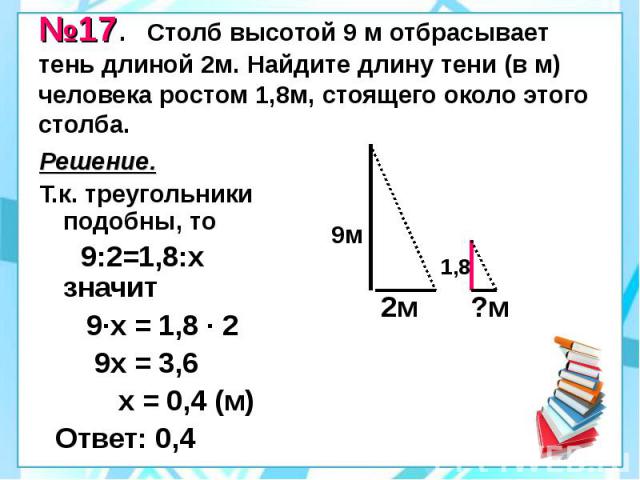
№17. Столб высотой 9 м отбрасывает тень длиной 2м. Найдите длину тени (в м) человека ростом 1,8м, стоящего около этого столба. Решение. Т.к. треугольники подобны, то 9:2=1,8:х значит 9·х = 1,8 · 2 9х = 3,6 х = 0,4 (м) Ответ: 0,4

№17. Самостоятельно Человек, рост которого 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина его тени равна 2 м. Определите высоту фонаря. Ответ:4

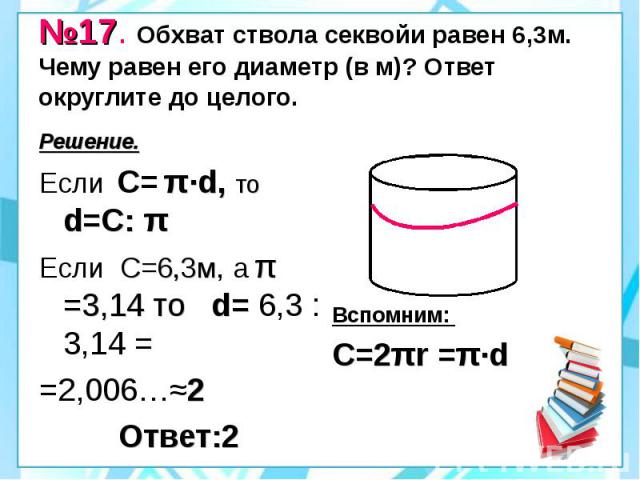
№17. Обхват ствола секвойи равен 6,3м. Чему равен его диаметр (в м)? Ответ округлите до целого. Решение. Если С= π·d, то d=С: π Если С=6,3м, а π =3,14 то d= 6,3 : 3,14 = =2,006…≈2 Ответ:2

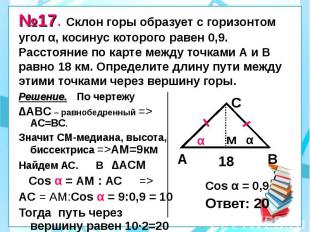
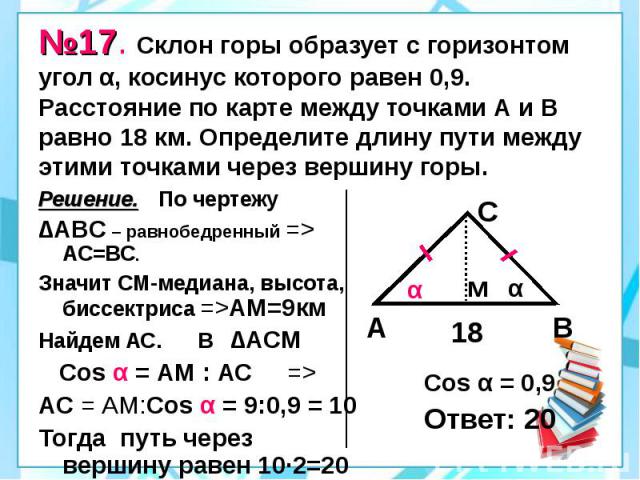
№17. Склон горы образует с горизонтом угол α, косинус которого равен 0,9. Расстояние по карте между точками А и В равно 18 км. Определите длину пути между этими точками через вершину горы. Решение. По чертежу ∆АВС – равнобедренный => АС=ВС. Значит СМ-медиана, высота, биссектриса =>АМ=9км Найдем АС. В ∆АСМ Cos α = АМ : АС => АС = АМ:Cos α = 9:0,9 = 10 Тогда путь через вершину равен 10·2=20 (км)

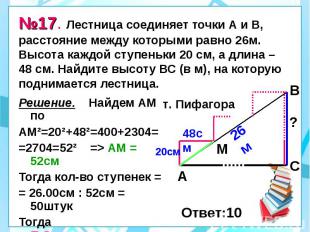
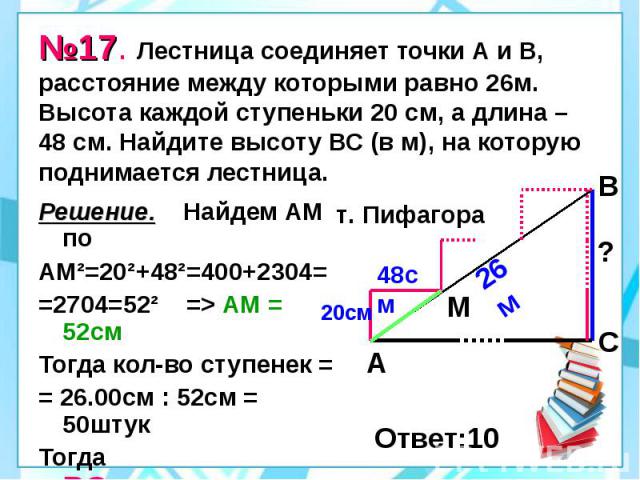
№17. Лестница соединяет точки А и В, расстояние между которыми равно 26м. Высота каждой ступеньки 20 см, а длина – 48 см. Найдите высоту ВС (в м), на которую поднимается лестница. Решение. Найдем АМ по АМ²=20²+48²=400+2304= =2704=52² => АМ = 52см Тогда кол-во ступенек = = 26.00см : 52см = 50штук Тогда ВС=50·20см=1000см= =10м.

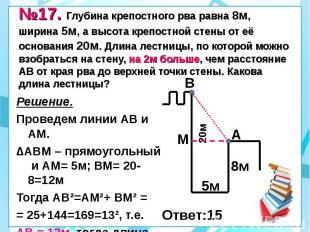
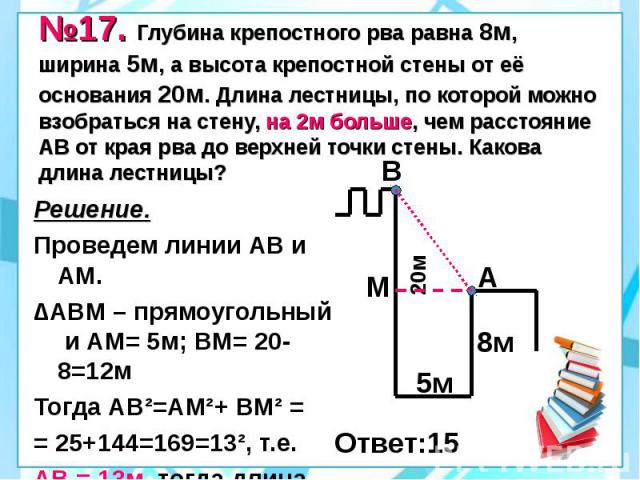
№17. Глубина крепостного рва равна 8м, ширина 5м, а высота крепостной стены от её основания 20м. Длина лестницы, по которой можно взобраться на стену, на 2м больше, чем расстояние АВ от края рва до верхней точки стены. Какова длина лестницы? Решение. Проведем линии АВ и АМ. ∆АВМ – прямоугольный и АМ= 5м; ВМ= 20-8=12м Тогда АВ²=АМ²+ ВМ² = = 25+144=169=13², т.е. АВ = 13м, тогда длина лестницы = 13+2=15м

№ 21. Упростить выражение Решение. Ответ:0,5

№ 21. Решить в парах 1) 2)

№ 22. Один из корней уравнения 4х² - х +3m = 0 равен 1. Найдите второй корень Решение. Если 1-корень уравнения, то можем подставить его в уравнение, т.е. 4·1² - 1 +3m = 0 => 3 +3m = 0 => 3m = - 3 => m = - 1. И данное уравнение примет вид: 4х² - х - 3 = 0 Решим его. т.к. а+в+с=0, то х1=1; х2= -3/4=-0,75 Ответ: второй корень данного уравнения 0,75

№ 22. Решить в парах Один из корней уравнения 5х² - 2х +3р = 0 равен 1. Найдите второй корень. Ответ: - 0,6 Один из корней уравнения 3х² +5х +2m = 0 равен - 1. Найдите второй корень Ответ: - 2/3

Используемые ресурсы