Презентация на тему: Системы счисления

Учитель информатики ГБОУ СОШ № 684 Демяшкевич Надежда Семеновна Системы счисления

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Система счисления: даёт представления множества чисел (целых и/или вещественных); даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление); отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на позиционные непозиционные смешанные

Позиционные системы счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам. В более поздний период такая нумерация была развита индусами и имела неоценимые последствия в истории цивилизации. К числу таких систем относится десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов.

Наиболее употребляемыми в настоящее время позиционными системами являются: 2 — двоичная (в дискретной математике, информатике, программировании); 3 — троичная; 8 — восьмеричная; 10 — десятичная (используется повсеместно); 12 — двенадцатеричная (счёт дюжинами); 13 — тринадцатеричная; 16 — шестнадцатеричная (используется в программировании, информатике); 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты). В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

Примеры систем счисления

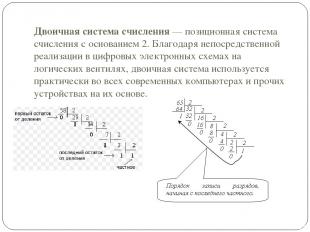
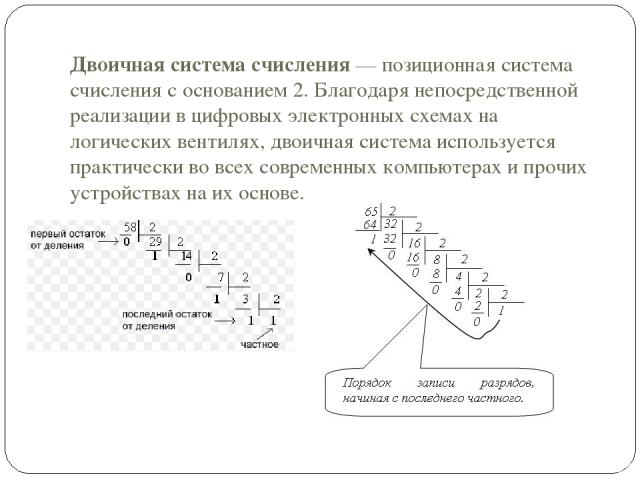
Двоичная система счисления — позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих устройствах на их основе.

В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».

Троичная система счисления Это  позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная. Примером представления чисел в несимметричной троичной системе счисления может служить запись в этой системе целых положительных чисел:

Восьмеричная система счисления Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7. Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

Шестнадцатеричная система счисления Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16 . Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

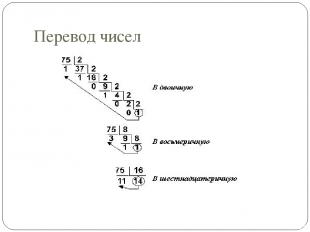
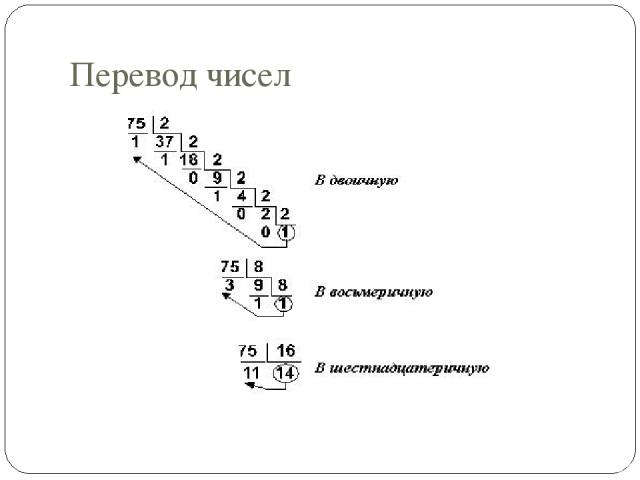
Перевод чисел