Презентация на тему: Древние системы счисления

Как люди считают? Древние системы счисления.

Оглавление Введение Цели и задачи Актуальность I. Возникновение чисел Как люди научились считать? Пальцевой счет Появление систем счисления. Древние системы счисления Системы счисления . Простая система счисления Непозиционные системы счисления Древнеегипетская десятичная Римская пятеричная Древнегреческая аттическая пятеричная Древнегреческая ионийская десятеричная Славянская десятеричная Древнеиндийские системы счисления Недостатки непозиционной системы счисления Позиционные системы счисления Вавилонская десятеричная/ шестидесятеричная Древнекитайская десятеричная Система счета у древних майя Двоичная система счисления Десятичная система счисления «История арабских чисел» Исследовательская работа «Главное число» Вывод

Цели и задачи Цель моего исследования: Исследовать происхождение чисел, древние системы счисления для того, чтобы объяснить учащимся. Для этого я решила поставить для себя несколько задач: Задачи моего исследования: Узнать происхождение цифр с самых древних времен. Как появились цифры, которыми пользуемся мы. Найти материал о каждой цифре. Какие системы счисления использовались в разные исторические периоды? Почему системы счисления актуальны сейчас и почему мы с ними знакомимся? Почему мы используем больше одной системы счисления? Как мы считаем? Где мы используем разные системы счисления?  

Современному человеку трудно представить себе математику без обозначений чисел и арифметических действий. Но ведь когда-то же этих обозначений не существовало. А тогда откуда они взялись? И почему именно такие, а не иначе? И вообще много ли их существовало? Ни для кого не секрет, что всюду и повсеместно каждое мгновение наша жизнь наполнена цифрами и числами: день недели, номер автомобиля, магазинный ценник, штрих-код на книжной обложке, количество калорий в пирожном и сколько дней осталось до каникул?.. Вся наша бытность состоит из арифметики, простой или сложной, у нас есть счастливые числа и памятные даты и мы не мыслим свою жизнь без количественной системы счисления. Мы никогда не задумываемся о значимости чисел в нашей культуре, общении и о том, что этим нехитрым знакам можно подчинить все на свете.

Как люди научились считать? Так говорили пифагорейцы ,подчеркивая необычно важную роль чисел в практической деятельности. Современный человек каждый день запоминает номера машин, телефонов, в магазине подсчитывает стоимость покупок, ведет семейный бюджет и т.д. Числа, цифры …они с нами везде. Люди всегда считали и записывали числа, даже пять тысяч лет назад. Но записывали они их совершенно по-другому, по другим правилам. Но в любом случае число изображалось с помощью любого или нескольких символов, которые называются числами. Лозунг «Все есть число»

Давным- давно, многие тысячи лет назад, наши далёкие предки жили небольшими племенами. Они бродили по полям, лесам, по долинам рек и ручьёв, разыскивая себе пищу. Питались листьями, плодами и корнями различных растений. Иногда ловили рыбу, собирали ракушки или охотились. Одевались в шкуры убитых зверей. Жизнь первобытных людей мало чем отличалась от жизни животных. Да и сами люди отличались от животных только тем, что … они владели речью и умели пользоваться простейшими орудиями труда: палкой или камнем, привязанным к палке. Первобытные люди, так же как и современные маленькие дети, не знали счёта. Но теперь детей учат считать родители и учителя, старшие братья и сёстры, товарищи. А первобытным людям не у кого было учится. Их учителем была сама жизнь. Поэтому и обучение шло медленно.

Наблюдая окружающую природу, от которой полностью зависела его жизнь, наш далекий предок из множества различных предметов сначала научился выделять отдельные предметы. Из стаи волков – вожака стаи. Из стада оленей – одного оленя. Поначалу они определяли это соотношение как «один» и «много». Частые наблюдения пары предметов, таких как: глаза, уши, рога, крылья, руки привели человека к представлению о числе. Наш далекий предок, рассказывая о том, что видел двух уток, сравнивал их с парой глаз. А если он видел их больше, то говорил: «много». Лишь постепенно человек научился выделять три предмета, ну а затем четыре, пять, шесть и т.д.

Учиться считать требовала жизнь. Добывая пищу, людям приходилось охотиться на крупных зверей: лося, медведя, зубра. Охотились наши предки большими группами, иногда всем племенем. Чтобы охота была удачной, нужно было уметь окружить зверя. Обычно старший ставил двух охотников за берлогой медведя, четырех с рогатинами – против берлоги для этого он должен был уметь считать, а так как названий чисел тогда еще не было, он показывал число на пальцах. Специальные названия чисел имелись поначалу только для одного и двух. Числа же больше двух называли с помощью сложения: 5 – это два, еще два и один.

Развитие счёта пошло значительно быстрее, когда человек догадался обратиться к самому близкому ему, самому естественному счётному аппарату – к своим пальцам. Быть может, первым актом счёта по пальцам было оказание предмета, указательным пальцем; тут палец сыграл роль единицы. Участие пальцев в счёте помогло человеку переступить за число четыре, так как когда все пальцы на одной руке стали считаться равноценными единицами, это сразу позволило довести счёт до пяти. Дальнейшее развитие счёта потребовало усложнения счётного аппарата, и человек нашёл выход, привлекая к счёту сначала пальцы второй руки, а затем распространяя свой приём на пальцы ног: для племён, не носивших обуви, использование пальцев ног было вполне естественным. При этом такое расширение счётных этапов, очевидно, произошло в следствии возможности привести в однозначное соответствие пальцы рук и ног, что и отмечается у некоторых народов.

II. Появление систем счисления. Древние системы счисления Переход человека к пальцевому счету привел к созданию нескольких различных систем счисления. Самой древней из пальцевых систем счисления считается пятеричная. Эта система, как полагают, зародилась и наибольшее распространение получила в Америке. Её создание относится к этой эпохе, когда человек считал по пальцам одной руки. Очевидно, при таком способе счета делался какой-нибудь всякий раз, когда заканчивался отсчет всех пальцев одной руки. До последнего времени у некоторых племен пятеричная система сохранилась еще в чистом виде (например, у жителей Полинезии и Меланезии). .

Дальнейшее развитие систем счисления пошло по двум путям. Племена, не остановившиеся на счете по пальцам на одной руке, перешли к счету по пальцам второй руки и далее – по пальцам ног. При этом часть племен остановилась на счете пальцев только на руках и этим положило основу для десятичной системы счисления, а другая часть племен, вероятно большая, распространила счет на пальцы ног и тем самым создало предпосылки на основание системы с основанием 20. Такая система получила распространение главным образом среди значительной части индейских племен Северной Америки и Туземных обитателей Центральной и Южной Америки, а так же в северной части Сибири и в Африке. Десятичная система счисления является преобладающей у народов Европы. Однако это не означает, что в Европе эта система всегда была единственной: некоторые народы перешли к десятичной системе уже в более поздние времена, а ранние пользовались другой системой.

Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр) вес цифры не зависит от её позиции в числе вес каждой цифры изменяется в зависимости от её положения Системы счисления непозиционные позиционные Единичная Двадцатеричная народов племени Майя Римская Вавилонская (цифры I, V, X, L, C, D, M) Древнеегипетская Древнекитайская десятеричная Древнегреческая Двоичная Славянская Десятичная кириллическая (0 1 2 3 4 5 6 7 8 9)

Единичная ("палочная”, “унарная”) система счисления НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

Унарные системы Число образуется путем повторения одного знака, символизирующего единицу. = Единичная система счисления 10 - 11 тыс. лет до н. э.

Древнеегипетская система счисления = 1205 НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ = 23029 Примерно  в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.  Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной. назад

,

Римская пятеричная НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века. В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число:MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника. Римскими цифрами  пользовались  очень долго.  Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами  (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.

9 = 10 -1 НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 12 = 10 + 1 + 1 Римская система счисления - для записи чисел используются буквы латинского алфавита Для записи чисел используются два правила: 1- каждый меньший знак, поставленный слева от большего, вычитается из него; 2- каждый меньший знак, поставленный справа от большего, прибавляется к нему. IX XII

Древнегреческие системы счисления НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Древнегреческая аттическая пятеричная = 256 = 2051 = 382 Древнегреческая ионийская десятеричная алфавитная = 265 = 503 = 731

Древнегреческая нумерация В V веке до н.э. появилась алфавитная нумерация.

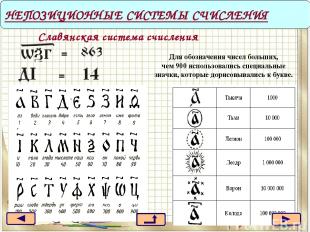
Славянская система счисления НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве.

НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Древнеиндийские системы счисления Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево. Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми, было то, что цифры от 4 до 90, были представлены только одним знаком.

Недостатки непозиционных системы счисления 1.    Существует постоянная  потребность введения новых знаков для записи больших чисел. 2.    Невозможно представлять дробные и отрицательные числа. 3.    Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов. Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.

Основание системы – это количество различных знаков, используемых для изображения чисел в данной системе. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Троичная 0, 1, 2 Пятеричная 0, 1, 2, 3, 4 Двенадцатеричная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B Позиция цифры в числе называется разрядом.

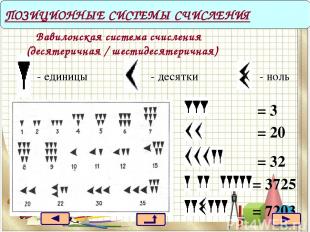
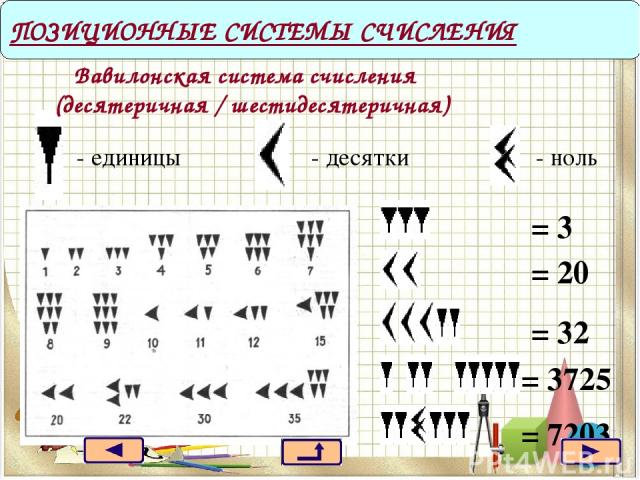
- единицы ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ - десятки - ноль Вавилонская система счисления (десятеричная / шестидесятеричная) = 3 = 20 = 32 = 7203 = 3725

Расцвет вавилонского государства относится ко второй половине XVIII в. до н.э. Продукты сельского хозяйства (зерно, фрукты, скот) являлись предметами вывоза в соседние страны. Торговле благоприятствовало центральное положение Вавилона на берегу судоходных рек. Расцвет торговли повлек за собой развитие денежной системы мер. В Вавилоне была создана система мер аналогичная нашей метрической, только в основе её лежало не число 10, а число 60. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.

Древнекитайская десятеричная система счисления Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде 1*1 000 = 1000 5 * 100+4* 10+8 = 548

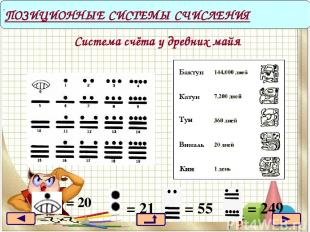
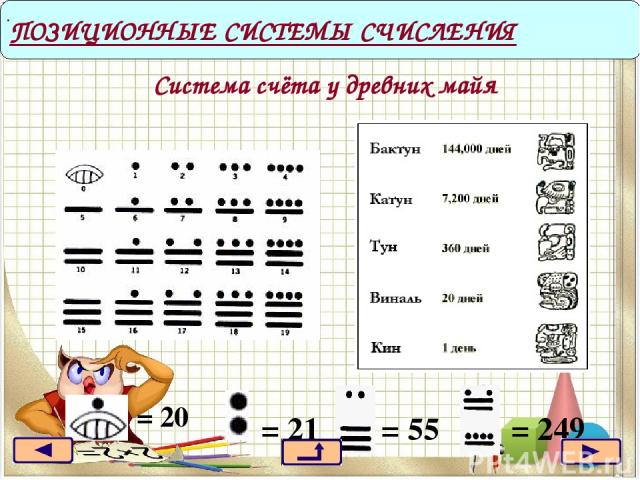
Система счёта у древних майя = 20 ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ . = 21 = 55 = 249

Двоичная система счисления 1 0 1 1 Используются две цифры – 0 и 1 Применяются в технических устройствах 1703г. – великий немецкий математик Лейбниц ввел в математику двоичную систему счисления. 1936-1938гг. – американский инженер и математик Клод Шеннон предложил использовать двоичную систему счисления для конструирования электрических схем.

ОБРАЗОВАНИЕ ЧИСЕЛ В ПСС 0 Первые десять целых чисел Десятичная система 0 1 2 3 4 5 6 7 8 9 Троичная система 0 1 2 10 11 12 20 21 22 100 Двенадцатеричная система 0 1 2 3 4 5 6 7 8 9 Пятеричная система 0 1 2 3 4 10 11 12 13 14 1 2… 9 1 1 1 2 2 0 1 … 9 0 1

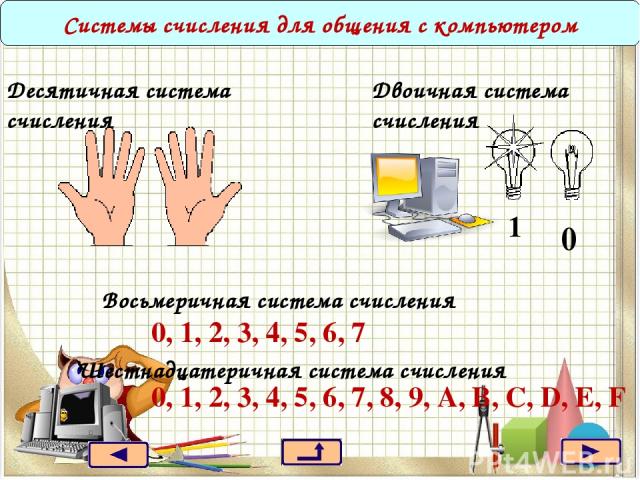
Системы счисления для общения с компьютером 1 0 Десятичная система счисления Двоичная система счисления Восьмеричная система счисления Шестнадцатеричная система счисления 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Десятичная система счисления Цифры 1234567890 сложились в Индии около 400 г. н. э. Арабы стали пользоваться подобной нумерацией около 800 г. н. э. Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.

Десятичная система счисления ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

История «арабских» чисел. История привычных «арабских» чисел запутана и возникла благодаря древним астрономам, их точным расчетам. Примерно во II веке до н.э. греческие астрономы познакомились с наблюдениями вавилонян, переняли их позиционную систему счисления. Целые числа они записывали не с помощью клиньев, а в своей алфавитной нумерации. Для обозначения нуля использовали первую букву греческого слова Ouden - ничто. Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией, переняв шестидесятеричную систему и круглый греческий нуль, соединили греческую нумерацию с десятичной мультипликативной системой взятой из Китая. Арабы, в свою очередь первыми оценили, усвоили и и перенесли ее в Европу, упростили знаки, и они приобрели вид , получив название арабской. В XII веке нашей эры она распространилась по всей Европе, так как была удобнее и проще. Слово «цифра» тоже перешло к нам от арабов по наследству нуль или «пусто», называли «сифра». Сейчас цифрами называются все десять знаков для записи чисел. История «арабских» чисел.

Первым по времени крупным математиком был у народов входивших в состав халифата, мы назовем великого узбекского (хорезмийского) математика и астролога IX в. Мухаммеда бен Мусса аль-Хорезми (2-я половина VIII в. – между 830-840).

Значение чисел по Пифагору Пифагор, его ученики и последователи сократили все числа до цифр от 1 до 9 включительно, так как они являются исходными числами, из которых могут быть получены все другие. Знаменитый Корнелиус Агриппа в своём труде "Оккультная философия", вышедшем в 1533 году, назвал эти числа и их значения.

Значение чисел по Пифагору Число 1 - число цели, которое проявляется в форме агрессивности и амбиции. Число 2 - число с крайностями. Оно поддерживает равновесие, смешивая позитивные и негативные качества. Число 3 - означает неустойчивость. Оно объединяет талант и весёлость и символизирует приспособляемость.

Значение чисел по Пифагору Число 4 - число означает устойчивость и прочность. Число 5 -символизирует риск. Это число является и самым счастливым, и самым непредсказуемым. Число 6 - символ надёжности. Оно находится в гармонии с природой. Это идеальное число.

Значение чисел по Пифагору Число 7 - число символизирует тайну, а так же изучение и знание. Число 8 - число материального успеха. Оно означает надёжность, доведённую до совершенства, равновесие. Число 9 - символ всеобщего успеха. Оно объединяет черты целой группы.

У каждого человека есть свое главное число. Мы решили сосчитать «главные числа» для всех учеников нашего класса и провели маленькое исследование. Свое «главное число» можно вычислить по дню, месяцу и году своего рождения. Например, я родилась 12 декабря 1979 года (12.12.1979). Складываем между собой все эти цифры: 1+2+1+2+1+9+7+9 и получаем 32. Две эти цифры тоже надо сложить между собой: 3+2= 5. «Пять» – это и есть мое главное число. Так мы сосчитали «главные числа» всех учащихся 6 класса. Исследования

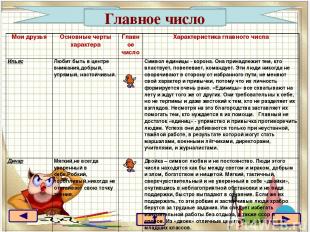
Главное число Мои друзья Основные черты характера Главное число Характеристика главного числа Ильяс Любит быть в центре внимания,добрый, упрямый, настойчивый. Символ единицы - корона. Она принадлежит тем, кто властвует, повелевает, командует. Эти люди никогда не сворачивают в сторону от избранного пути, не меняют свой характер и привычки, потому что их личность формируется очень рано. «Единицы» все схватывают на лету и ждут того же от других. Они требовательны к себе, но не терпимы и даже жестокий к тем, кто не разделяет их взглядов. Несмотря на это благородства заставляет их помогать тем, кто нуждается в их помощи. Главный не достаток «единиц» - упрямство и привычка противоречить людям. Успеха они добиваются только при неустанной, тяжёлой работе, в результате которой могут стать маршалами, военными лётчиками, директорами, учителями, и журналистами. Динар Мягкий,не всегда уверенный в себе.Робкий, торопливый,никогда не отстаивает свою точку зрения. Двойка – символ любви и не постоянство. Люди этого числа находятся как бы между светом и мраком, добрым и злом, богатством и нищетой. Мягкий, тактичный, сверхчувствительный и не уверенный в себе «двойки», очутившись в неблагоприятной обстановки и не видя поддержки, быстро выпадают в отчаяние. Если же их поддержать, то эти робкие и застенчивые люди храбро берутся за трудные задания. Им следует избегать изнурительной работы без отдыха, а также ссор и споров. Из «двоек» отличные целители, врачи,учителя младших классов.

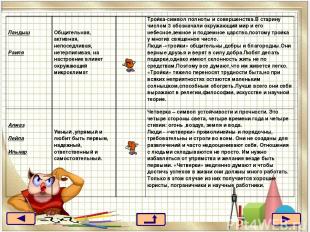
Ландыш Раиля Общительная, активная, непоседливая, нетерпиливая, на настроение влияет окружающий микроклимат Тройка-символ полноты и совершенства.В старину числом 3 обозначали окружающий мир и его небесное,земное и подземное царство,поэтому тройка у многих священное число. Люди -«тройки» общительны,добры и благородны.Они верные друзья и верят в силу добра.Любят делать подарки,однако имеют склонность жить не по средствам.Поэтому все думают,что им живется легко. «Тройки» тяжело переносят трудности быта,но при всяких неприятностях остаются маленьким солнышком,способным обогреть.Лучше всего они себя выражают в релегии,философии, искусстве и научной теорие. Алмаз Лейла Ильнар Умный ,упрямый и любит быть первым, надежный, ответственный и самостоятельный. Четверка – символ устойчивости и прочности. Это четыре стороны света, четыре времени года и четыре стихии: огонь ,воздух, земля и вода. Люди - «четверки» прямолинейны и порядочны, требовательны и строги во всем. Они не созданы для развлечений и часто недооценивают себя. Отношения с людьми складываются не просто. Им нужно избавляться от упрямства и желания везде быть первыми. «Четверки» медленно думают и чтобы достичь успехов в жизни они должны много работать. Только в этом случае из них получается хорошие юристы, пограничники и научные работники.

Гульнара Очень любит путешествовать, «загорается» новыми идеями. Он смелый, сильный и не боится трудностей,у него много друзей. Пятерка- символ власти. Путь этих людей труден и полон случайностей. Их постоянно влекут новые места,события и идеи.Они быстры ,сметливы,не боятся трудностей,но не переносят однообразия ,поэтому любят начинать новые дела. «Пятерки» доброжелательны и у них много друзей, и везде они себя чувствуют как дома.Однако главный недостаток неумение и нетерпение слушать других. Они любят рисковать и хорошо проявляют себя будучи предпринимателями,журналистами. Настя Трудолюбивый,добрый, самостоятельный, имеет свое мнение, стараясь его отстоять к лидерству не стремится. Шестерка- символ гармонии. Это число независимых, трудолюбивых людей. У них тонкий вкус,они понимают и ценят прекрасное, а богатое воображение делает их жизнь красочной и насыщенной.Прощая слабость другим,они нередко идут по жизни легким путем,получая как можно больше удовольствий. У них всегда есть свое мнение,но они не стремятся стать лидерами, потому что не переносят конфликтов и споров.Если слова не будут расходиться с делом, «шестерки» станут известными в обществе. Ляля Спокойная, мечтательная, старательная, любит похвалу, любознательная. Семерка- символ загадочности и тайны.У людей этого числа повышенная духовность.Им снятся фантастические сны, чудятся неведомые запахи, и все это они толкуют по- своему.Они всегда заняты собой.Часто теряются и не понимают даже самих себя, поэтому нуждаются в умных и тонко чувствующих людях.Характер у «семерок» неуравновешенный,взрывной.Они не выносят критики, но любят похвалу.Их интересует история,искусство, загадки человеческой души и не волнует заработок.

Лейсан Спокойная,с завышенной самооценкой,непостоянная,но любит участвовать в самодеятельности. Восьмерка- символ бесконечности.Люди этого числа обречены на вечную борьбу с собой.Капризные и не постоянные, они предъявляют к себе очень высокие требования.Такие же требования предъявляют они без всякого снисхождения к другим.Их не легко сломать.Они независимы, и делают все по- своему. «Восьмерок» часто подстерегают потери и унижения, но в делах им многое удается.Умеют увлечь за собой коллектив и отлично проявляют себя в политике,деловом мире и искусстве. Талия Подвижная, не всегда ответственная в работе, жизнерадостная, спортивная. Девятка – символ воинственности. Это бойцы, если войны нет, они превращают в битву саму жизнь. Вспыльчивые, резкие безрассудные «девятки или строят или разрушают. Отношения с окружающими сложные. Если в чем-то ошибаются, обвиняют кого угодно, только не себя. У них много друзей, и много врагов, поэтому следует воспитать в себе доброту и уважения к другим. Из них получаются хорошие военные, спортсмены, цирковые артисты, летчики-испытатели, каскадеры и разведчики.

Вывод Еще с глубокой древности разные народы записывали цифры по-своему с помощью соответствующих символов. Существовали и существуют системы счисления с разными основаниями; Измерение времени и градусной меры углов основывается на шестидесятеричной системе счисления древних шумеров (Вавилон). На использование двенадцатеричной системы счисления в прошлом указывают названия числительных: год состоит из 12 месяцев, половина суток - из 12 часов; в русском языке счет идет дюжинами и гроссами ( по 144 = 122 ); сервизы, салфетки, столовые приборы, продают наборами по 6 или 12 штук. Десятичная система счисления впервые появилась в Индии. Персидский математик Аль-Хорезми изложил основы десятичной системы счисления.

Информационные ресурсы Числа Судьбы: пифагорейская, индийская и китайская нумерология.-Составление, предисловие Андрея Костенко. С.-Пб., "Экслибрис", 2003  И. Я. Депман Мир чисел: рассказы о математике: Дет. лит., 1982 г. А. Ликум Все обо всем. Популярная энциклопедия для детей – М.: Филологическое общество «Слово», 1993 г., том 1,7,9. А. Лопатина Добрая математика. М: «Амрита Русь» 2004г. Интернет-ресурсы. http://school-collection.edu.ru http://goldlara.narod.ru http://www.bigpi.biysk.ru/