Презентация на тему: Основы логики

Основы логики На рисунке – памятник Аристотелю (в городе Стагир – Греция, место его рождения) Презентация создана учителем математики и информатики Ковалевой Анной Леонидовной ГБОУ СОШ №341 г.СПб 2013-2014

ЛОГИКА (от греч. «логос» слово и смысл) – наука о закономерностях, формах и операциях мышления Т.е. это наука о том, как правильно рассуждать, делать выводы, доказывать утверждения. Наука логики известна еще с глубокой древности. Ее родоначальником был древнегреческий философ Аристотель (382-322 гг. до н.э.). Он ввел основные формы абстрактного мышления или так называемой формальной логики.

Со времен Аристотеля логика ушла не слишком далеко вперед. Даже немецкий философ Эммануил Кант (1724-1804) считал, что эта наука полностью завершила свое развитие. Однако немецкий философ, математик, физик, изобретатель, юрист, историк, лингвист Лейбниц (Готфрид Вильгельм,1646-1716) предпринял попытку логических вычислений). Идеи Лейбница о математической логике не заинтересовали его современников.

Потребовалось еще полтора столетия, пока в трудах английского математика Джорджа Буля (1815-1864) появился алфавит, орфография и грамматика для математической логики. Интересно, что Буль не имел математического образования.

Понятие – это форма мышления, отражающая наиболее существенные признаки предмета, отличающие его от других предметов Высказывание – это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними. Высказывание – это повествовательное предложение, про которое можно однозначно сказать, что оно истинно или ложно. Высказывания бывают: простыми (если никакая его часть сама не является высказыванием) сложными(составными) (это высказывание, состоящее из простых высказываний) Умозаключение – это форма мышления, посредством которой из одного или нескольких высказываний (ПОСЫЛОК) по определенным правилам получаются новые знания о предметах реального мира (ВЫВОДЫ). Умозаключения бывают дедуктивные, индуктивные, по аналогии. Логика – это наука о формах и способах мышления

ВИДЫ УМОЗАКЛЮЧЕНИЙ В дедуктивных умозаключениях рассуждения ведутся от общего к частному. (Примеры: «Все металлы электропроводны», «Ртуть является металлом», «Ртуть электропроводна») Приведите примеры дедуктивных умозаключений 2. В индуктивных умозаключениях рассуждения ведутся от частного к общему. (Примеры: Отдельные металлы – железо, медь, цинк, алюминий обладают свойством теплопроводности, следовательно можно сделать вывод, что все металлы электропроводны) Приведите примеры индуктивных умозаключений 3. Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений Пример: химический состав Солнца и Земли сходен по многим показателям, поэтому когда на Солнце обнаружили новый элемент гелий, то по аналогии заключили, что такой элемент есть и на Земле

Выбрать истинные высказывания: 1. Сумма углов треугольника равна 180 градусов 2. Основы формальной логики заложил Аристотель 3. Все углы равностороннего треугольника равны 60 градусов 4. Все стороны равнобедренного треугольника равны 5. У ромба не все стороны равны 6. Диагонали ромба взаимно перпендикулярны 7. Все металлы электропроводны Привести 10 ложных высказываний из различных областей жизни Сделать из предложенных суждений высказывание 1. «Все металлы электропроводны» 2. «Ртуть является металлом» 1. Гипотенуза и катет – элементы в прямоугольном треугольнике 2. Гипотенуза больше катета 1. «Сократ – отец Софроникса» 2. «Софроникс – сын Ксантиппы»

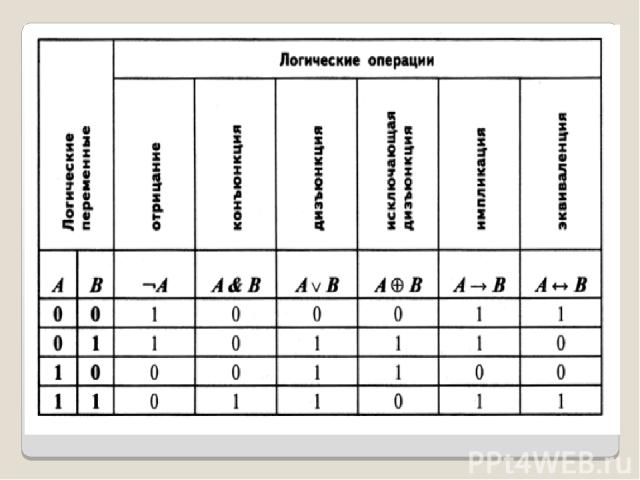
ЛОГИЧЕСКИЕ ОПЕРАЦИИ

ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «НЕ» Название: логическое отрицание (инверсия): Обозначение в булевой алгебре: ¬А Читается: частица НЕ Обозначение в языках программирования: not А (Паскаль, Бейсик) !А (Си) Логическое отрицание истинное высказывание(1) превращает в ложное (0), а ложное высказывание (0) в истинное (1). Таблица истинности логической операции инверсия (таблица истинности – это таблица, в которой слева перечисляются всевозможные значения исходного высказывания 0 или 1, а в правой части в последнем столбце записывают результат выполнения логической операции для каждого из этих вариантов)

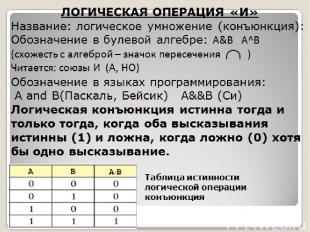
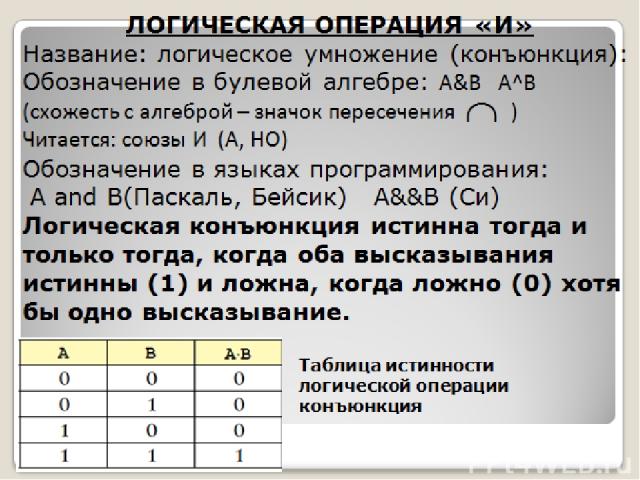
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «И» Название: логическое умножение (конъюнкция): Обозначение в булевой алгебре: А&B A^B (схожесть с алгеброй – значок пересечения ) Читается: союзы И (А, НО) Обозначение в языках программирования: А and B(Паскаль, Бейсик) А&&B (Си) Логическая конъюнкция истинна тогда и только тогда, когда оба высказывания истинны (1) и ложна, когда ложно (0) хотя бы одно высказывание. Таблица истинности логической операции конъюнкция

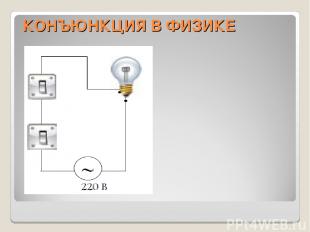
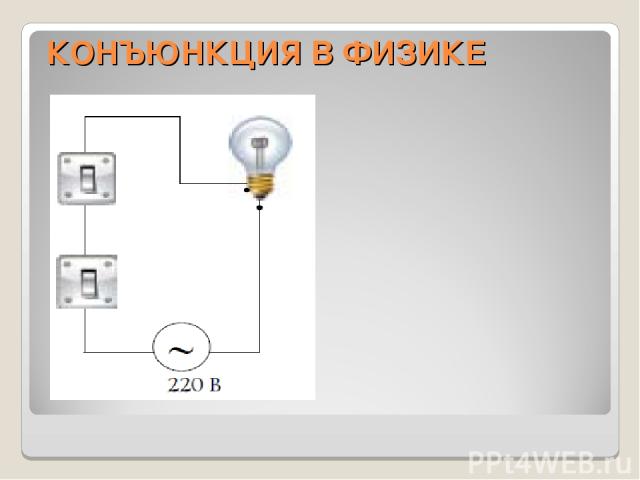
КОНЪЮНКЦИЯ В ФИЗИКЕ

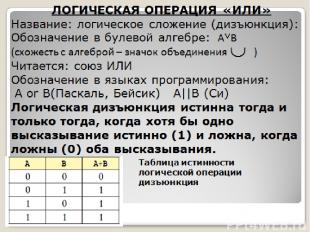
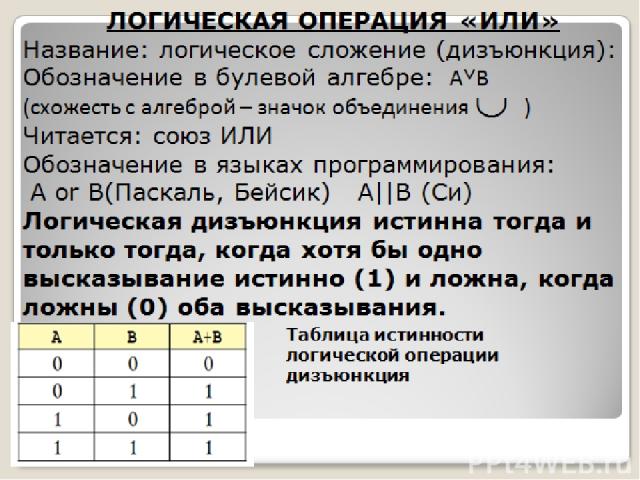
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «ИЛИ» Название: логическое сложение (дизъюнкция): Обозначение в булевой алгебре: A˅B (схожесть с алгеброй – значок объединения ) Читается: союз ИЛИ Обозначение в языках программирования: А or B(Паскаль, Бейсик) А||B (Си) Логическая дизъюнкция истинна тогда и только тогда, когда хотя бы одно высказывание истинно (1) и ложна, когда ложны (0) оба высказывания. Таблица истинности логической операции дизъюнкция

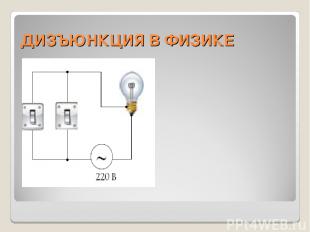
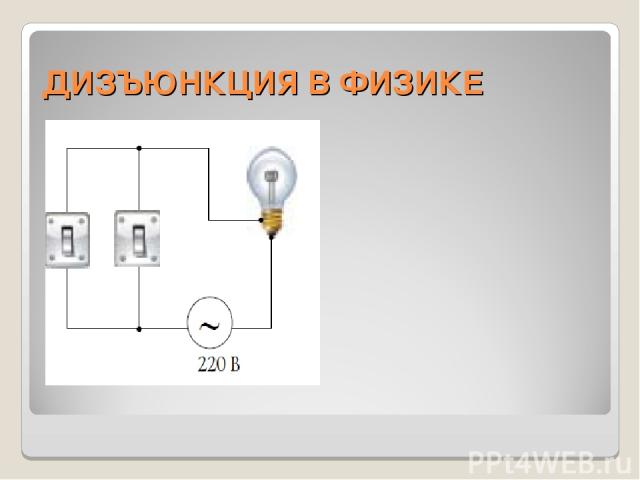
ДИЗЪЮНКЦИЯ В ФИЗИКЕ

ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «ИСКЛЮЧАЮЩЕЕ ИЛИ» Название: сложение по модулю 2 (разделительная дизъюнкция) Обозначение в булевой алгебре: A B А В Читается: оборот «или только…, или только …» Обозначение в языках программирования: А xor B(Паскаль) А^B (Си) Логическое сложение по модулю 2 истинно (1) тогда и только тогда, когда высказывания не равны и ложно (0), когда высказывания одинаковы. Таблица истинности логической операции исключающее или

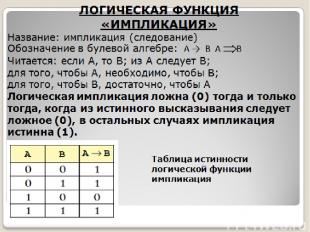
ЛОГИЧЕСКАЯ ФУНКЦИЯ «ИМПЛИКАЦИЯ» Название: импликация (следование) Обозначение в булевой алгебре: A → B А В Читается: если А, то В; из А следует В; для того, чтобы А, необходимо, чтобы В; для того, чтобы В, достаточно, чтобы А Логическая импликация ложна (0) тогда и только тогда, когда из истинного высказывания следует ложное (0), в остальных случаях импликация истинна (1). Таблица истинности логической функции импликация

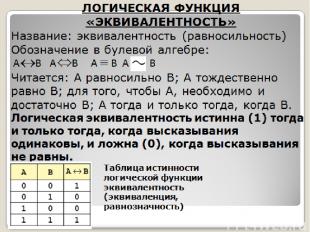
ЛОГИЧЕСКАЯ ФУНКЦИЯ «ЭКВИВАЛЕНТНОСТЬ» Название: эквивалентность (равносильность) Обозначение в булевой алгебре: A B А В А B А B Читается: А равносильно В; А тождественно равно В; для того, чтобы А, необходимо и достаточно В; А тогда и только тогда, когда B. Логическая эквивалентность истинна (1) тогда и только тогда, когда высказывания одинаковы, и ложна (0), когда высказывания не равны. Таблица истинности логической функции эквивалентность (эквиваленция, равнозначность)

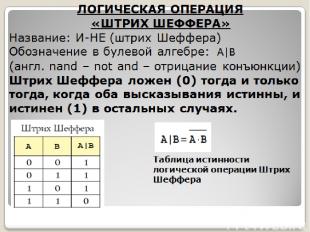
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «ШТРИХ ШЕФФЕРА» Название: И-НЕ (штрих Шеффера) Обозначение в булевой алгебре: A|B (англ. nand – not and – отрицание конъюнкции) Штрих Шеффера ложен (0) тогда и только тогда, когда оба высказывания истинны, и истинен (1) в остальных случаях. Таблица истинности логической операции Штрих Шеффера

ЛОГИЧЕСКАЯ ОПЕРАЦИЯ «СТРЕЛКА ПИРСА» Название: ИЛИ-НЕ (стрелка Пирса) Обозначение в булевой алгебре: A B или А B (англ. nor – not or – отрицание дизъюнкции) Стрелка Пирса истинна (1) тогда и только тогда, когда оба высказывания ложны, и ложна (0) в остальных случаях. Таблица истинности логической операции стрелка Пирса

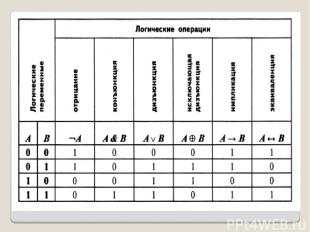
ПРИОРИТЕТ ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ: 1) В СКОБКАХ 2) НЕ 3) И 4) ИЛИ, 5) ИСКЛЮЧАЮЩЕЕ ИЛИ 6) ИМПЛИКАЦИЯ 7) ЭКВИВАЛЕНТНОСТЬ

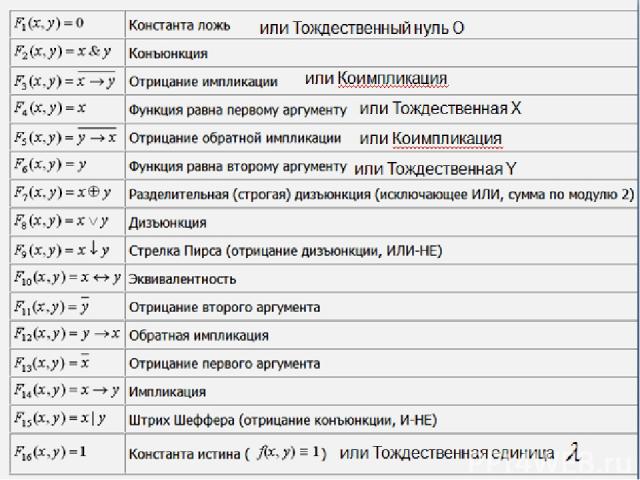
Любую логическую формулу можно рассмотреть как функцию F (x1,x2, …, xn). Существует 16 различных функций от двух переменных.

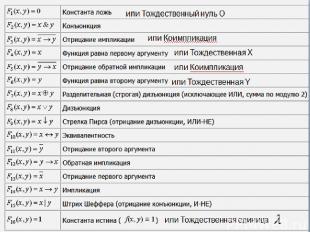
или Тождественный нуль O или Коимпликация или Тождественная Х или Коимпликация или Тождественная Y или Тождественная единица

ЛОГИЧЕСКИЕ ЗАКОНЫ: 1) ¬¬A=A Закон двойного отрицания 2) A˅ A=A Законы идемпотентности A&A=A 3) A ˅ 0=A Законы 0 и 1 (Законы исключения констант) A ˅ 1=1 A&0=0 A&1=A 4) A ˅(A&B) = A (Законы поглощения) A& (A ˅ B) = A 5) A ˅ ¬A = 1 (Закон исключения третьего) A & ¬A = 0 (Закон непротиворечия)  6) A & B = B & A  (Законы коммутативности или A ˅ B = B ˅ A переместительные законы)  7) A & (B& C) = (A & B) & C = A & B & C  (Законы ассоциативности или A ˅(B ˅ C) = (A ˅ B) ˅ C =A ˅ B ˅ C   сочетательные законы)  8) ¬ (A ˅ B) = ¬А & ¬В (Законы де Моргана – названы в честь шотландского  ¬ (A & B) = ¬А ˅  ¬В математика и логика де Моргана)  9) A & (B ˅ C) = (A & B) ˅ (A & C) (Законы дистрибутивности или A ˅ (B & C )= (A ˅ B) & (A  ˅ C)  распределительные законы)  10) A → B = ¬A ˅ B 11) A B = (A → B) & (B → A) = (A & B) ˅ (¬A & ¬B) = (А ˅¬В)&(¬A ˅B) 12) A B = (A&¬B) ˅ (¬A&B)

Тождественно истинная формула (тавтология) – это формула, которая принимает значение истина при любых значениях входящих в нее переменных. Тождественно ложная формула – это формула, которая принимает значение ложь при любых значениях входящих в нее переменных. Совершенная дизъюнктивная нормальная форма (СДНФ) – это логическая формула, в которой используются только операции отрицания (¬), конъюнкции (&), дизъюнкции (˅) при следующих условиях: отрицание применяется только к переменным; конъюнкцией соединены переменные или их отрицания, причем каждая переменная в таком конъюнктивном выражении фигурирует ровно один раз; дизъюнкции соединяют получившиеся конъюнктивные выражения. В силу договоренности о порядке выполнения операций в СДНФ скобки не требуются.

КВАНТОРЫ В математической логике наряду с логическими операциями используются и кванторы. Квантор (от лат. quantum — сколько) — логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате ее применения. В обычном языке носителями таких характеристик служат слова типа все, каждый, некоторый, любой, всякий, бесконечно много, существует, имеется, единственный, несколько, конечное число, а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным кванторов двух видов: квантора общности и квантора существования.

КВАНТОРЫ При построении отрицания к высказыванию, содержащему квантор, действует следующее правило: частица “не” добавляется к сказуемому, квантор общности заменяется на квантор единственности и наоборот. Рассмотрим пример. Отрицанием высказывания “Все юноши 11-х классов — отличники” является высказывание “Неверно, что все юноши 11-х классов — отличники” или “Некоторые юноши 11-х классов — не отличники”.

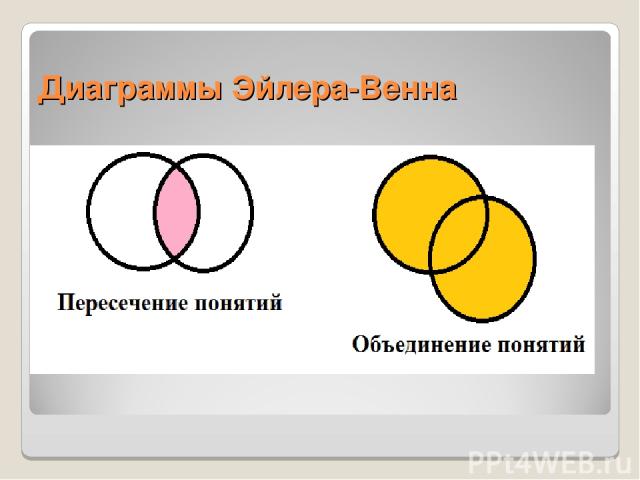
Диаграммы Эйлера-Венна

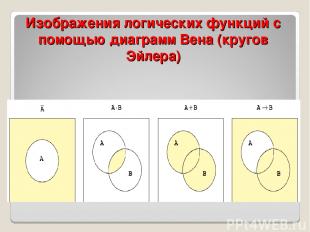
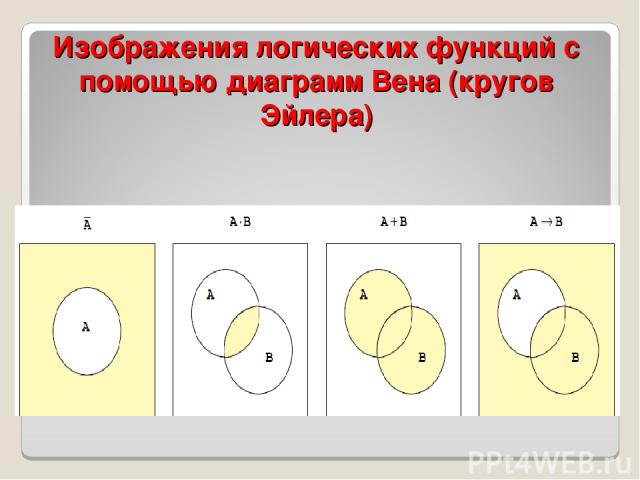
Изображения логических функций с помощью диаграмм Вена (кругов Эйлера)