Презентация на тему: Основы логики и логические основы построения компьютера

Высказывание состоит из понятий, и его можно сравнить с арифметическим выражением. В математической логике рассматриваются предикаты, т. е. функциональные зависимости от неопределённых понятий (терминов), которые можно сравнить с переменными в уравнении. Высказывание состоит из понятий, и его можно сравнить с арифметическим выражением. В математической логике рассматриваются предикаты, т. е. функциональные зависимости от неопределённых понятий (терминов), которые можно сравнить с переменными в уравнении.

НЕ (логическое отрицание, инверсия) НЕ (логическое отрицание, инверсия) ИЛИ (логическое сложение, дизъюнкция) И (логическое умножение, конъюнкция) Операция «ЕСЛИ - ТО» (логическое следование, импликация) Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

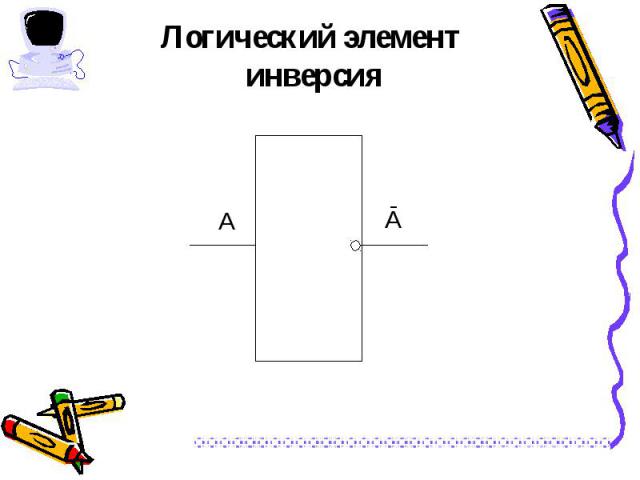
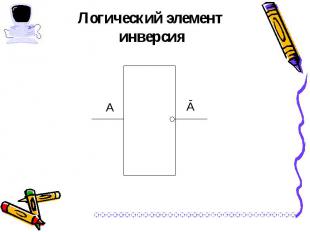
Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Обозначение операции НЕ, Ā, not А, ¬ А.

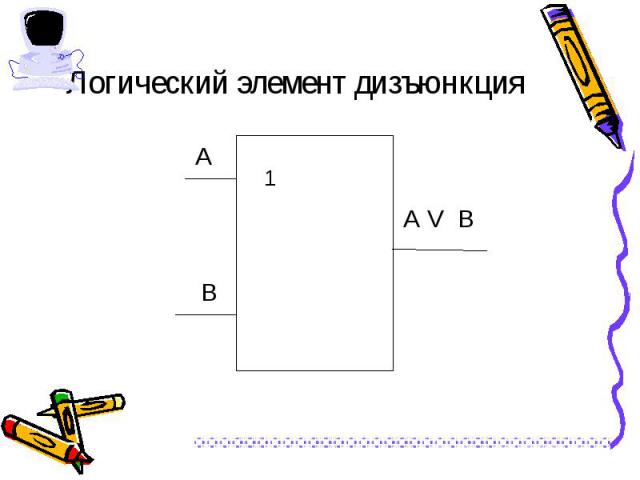
Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Обозначения операции: А или В, А or В, А V В.

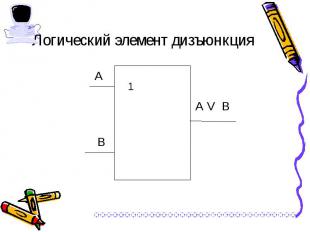
Обозначения операции: А xor В, А · В. Обозначения операции: А xor В, А · В.

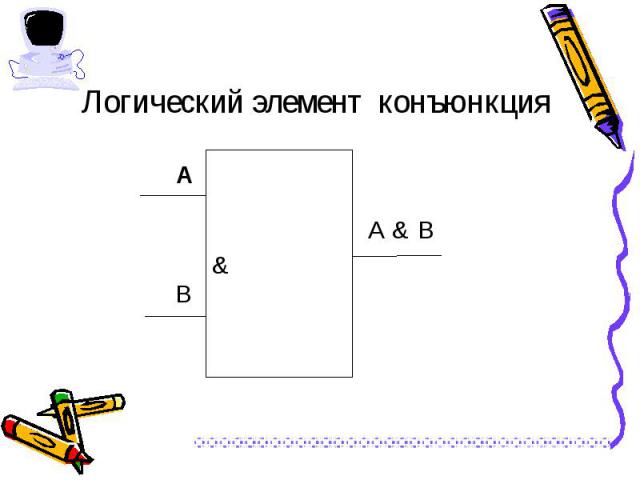
Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Обозначения операции: А и В, А & В, А and В, А Λ В.

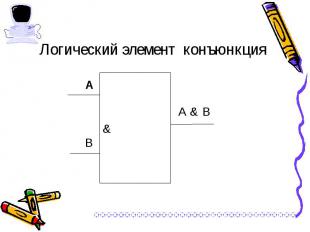
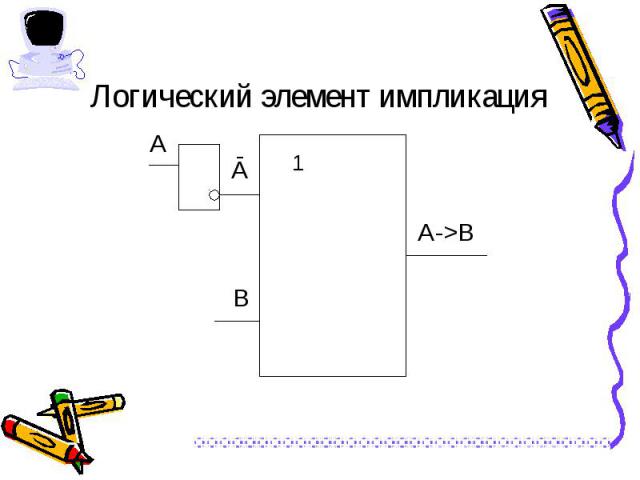
Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия. Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия. Обозначения операции: если А, то В; А влечет В; if A then B; А -> В; А => В

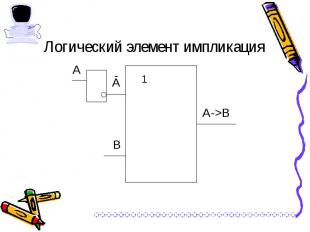
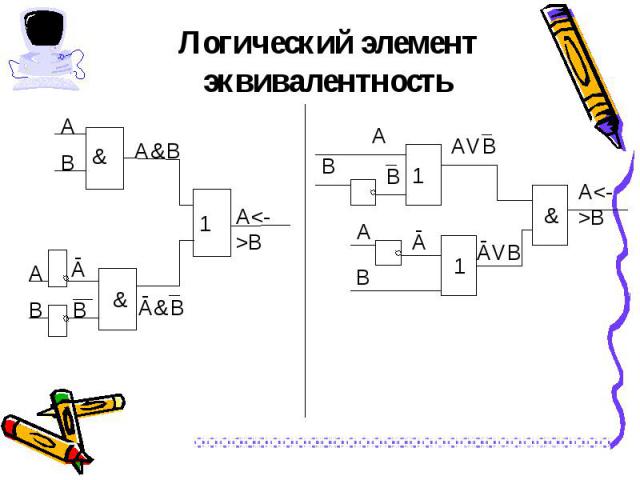
Обозначения операции: А ~ В, А <=> В, А Ξ В Обозначения операции: А ~ В, А <=> В, А Ξ В Результат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны.

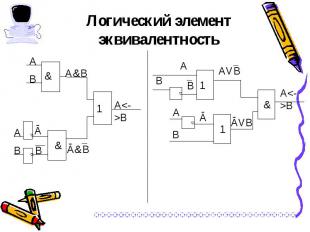
действия в скобках действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность

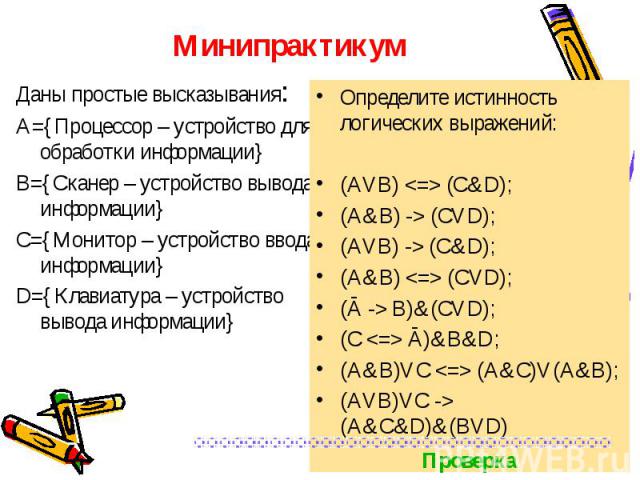
Даны простые высказывания: Даны простые высказывания: A={Процессор – устройство для обработки информации} B={Сканер – устройство вывода информации} C={Монитор – устройство ввода информации} D={Клавиатура – устройство вывода информации}

(AVB) <=> (C&D) = 0 (AVB) <=> (C&D) = 0 (A&B) -> (CVD) = 1 (AVB) -> (C&D) = 0 (A&B) <=> (CVD) = 1 (Ā -> B)&(CVD) = 0 (C <=> Ā)&B&D = 0 (A&B)VC <=> (A&C)V(A&B) = 1 (AVB)VC -> (A&C&D)&(BVD) = 0

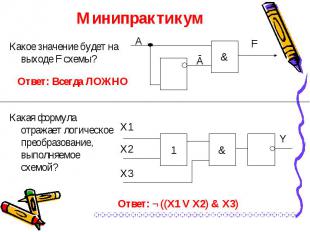
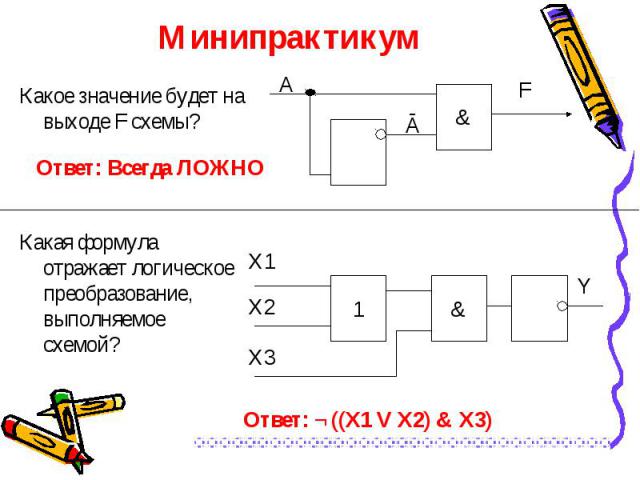
Какое значение будет на выходе F схемы? Какое значение будет на выходе F схемы?

Создание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций: Создание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций: Конъюнкции Дизъюнкции Инверсии Импликации Эквивалентности

Количество строк - 2ⁿ, где n- это количество логических переменных Количество строк - 2ⁿ, где n- это количество логических переменных Количество столбцов - количество логических переменных + количество логических операций. Пример: Ā&В Количество строк = 22 = 4 Количество столбцов = 2 + 2 = 4

(А В) (А В)=А (А В) (А В)=А (А В) (А В)=А

А (А В)= А А (А В)= А А (А В)=А А (Ā В)=А В А (Ā В)=А В