Презентация на тему: ОСНОВЫ ЛОГИКИ ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА

Основы логики и логические основы компьютера. Формы мышления.

Логика –это наука о формах и способах мышления;особая форма мышления. Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта. Высказывание – форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.

Логика Высказывания: Истинные(1) и ложные (0); Простые и сложные; Общие, частные и единичные.

Высказывания. Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается ( или можно начать) со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.

Примеры высказываний: Пример 1. Определить тип высказывания (общее, частное, единичное). «Все рыбы умеют плавать». Ответ: общее высказывание. «Некоторые медведи -бурые». Ответ: частное высказывание. «Буква А – гласная». Ответ: единичное высказывание.

Примеры высказываний: Пример 2. Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ»: Все ученики изучают математику. Все ученики изучают литературу. Все ученики изучают математику и литературу.

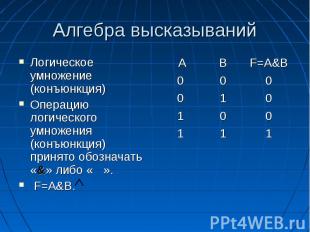
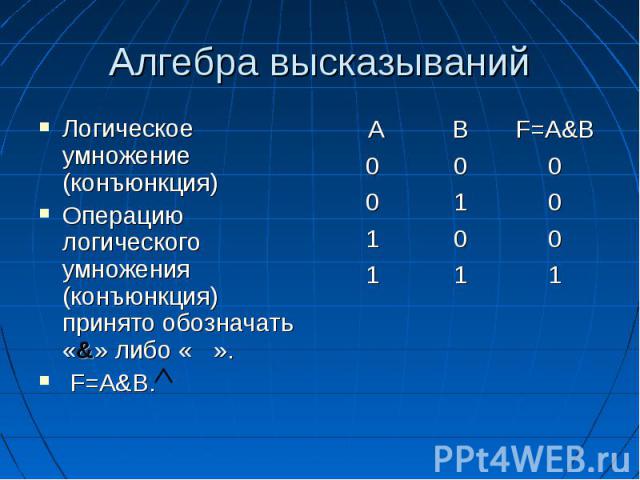
Алгебра высказываний Логическое умножение (конъюнкция) Операцию логического умножения (конъюнкция) принято обозначать «&» либо « ». F=A&B.

Логическое сложение Дизъюнкция Истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний. F=A B

Логическое отрицание. Инверсия Делает истинное высказывание ложным и, наоборот, ложное – истинным.

Логические законы и правила преобразования логических выражений. Закон тождества. Всякое высказывание тождественно самому себе. Закон непротиворечия.

Логические законы и правила преобразования логических выражений. Закон исключения третьего. Закон двойного отрицания. Закон де Моргана.

Логические законы и правила преобразования логических выражений. Закон коммутативности. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

Логические законы и правила преобразования логических выражений. Закон ассоциативности. Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять:

Логические законы и правила преобразования логических выражений Закон дистрибутивности. В алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:

Логические основы устройства компьютера Базовые логические элементы. Логический элемент «И» - логическое умножение. Логический элемент «ИЛИ» - логическое сложение. Логический элемент «НЕ» - инверсия.

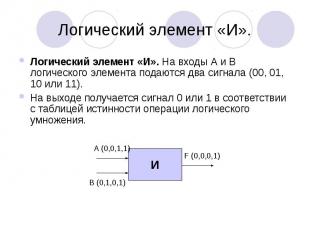
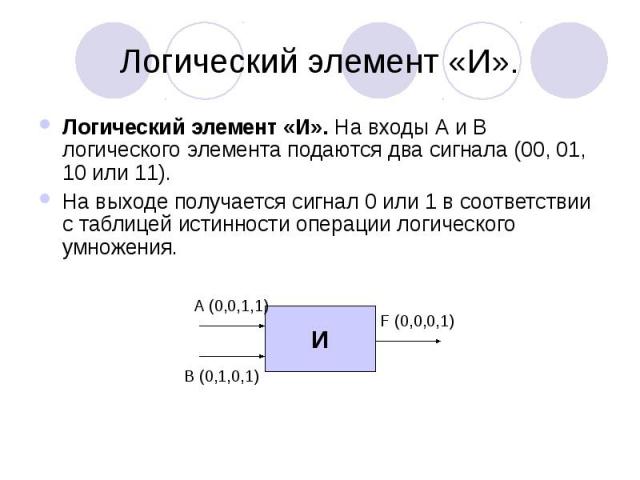
Логический элемент «И». Логический элемент «И». На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.

Логический элемент «ИЛИ». На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11). На входе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.

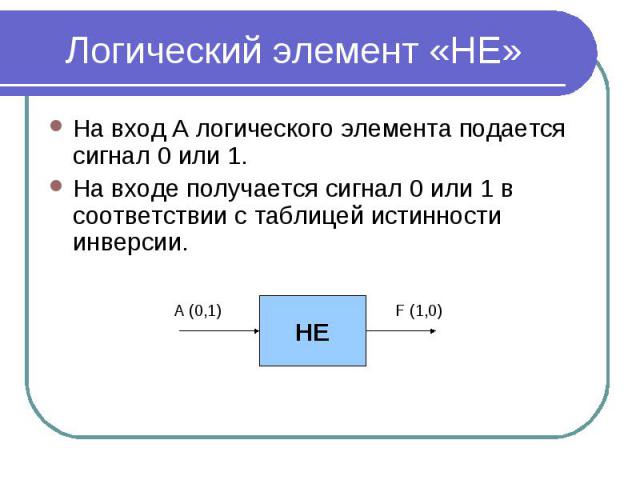
Логический элемент «НЕ» На вход А логического элемента подается сигнал 0 или 1. На входе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.

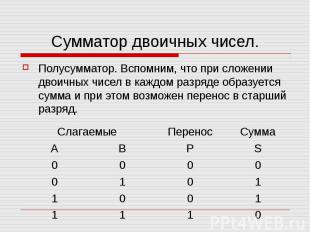
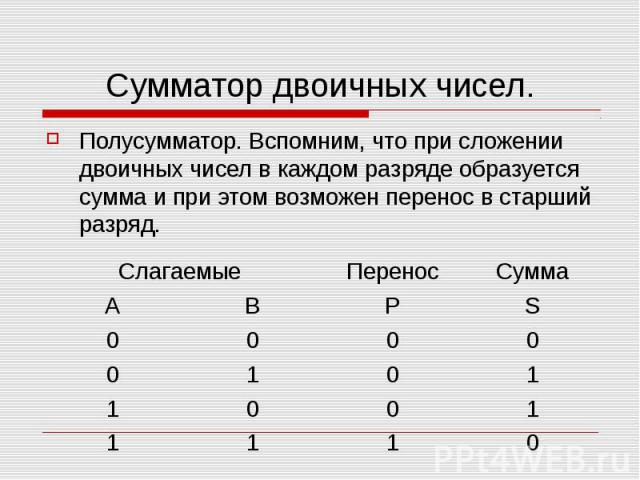
Сумматор двоичных чисел. Полусумматор. Вспомним, что при сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд.

Сумматор двоичных чисел Таблица истинности логической функции

Полный однозарядный сумматор. Полный однозарядный сумматор должен иметь три входа: А,В- слагаемые и Р0 – перенос из младшего разряда и два выхода: сумму S и перенос Р. Идея построения полного сумматора точно такая же, как и полусумматора. Перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных. Формула переноса получает следующий вид:

Многозарядный сумматор процессора состоит из полных однозарядных сумматоров. Многозарядный сумматор процессора состоит из полных однозарядных сумматоров. На каждый разряд ставится однозарядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.

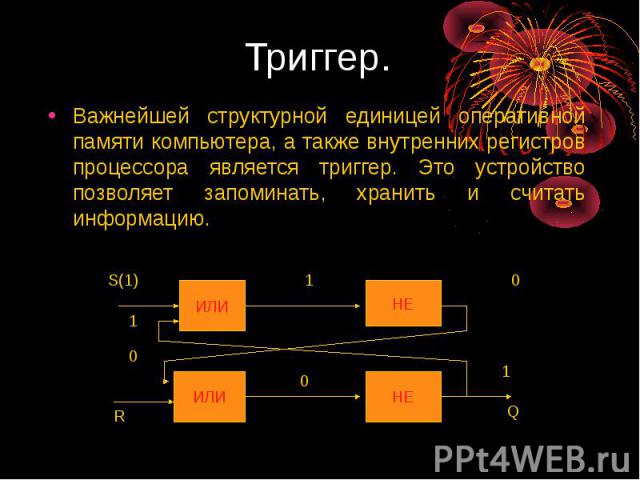
Триггер. Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считать информацию.