Презентация на тему: Некоторые элементарные приёмы теории графов при решении отдельных задач

Некоторые элементарные приёмы теории графов при решении отдельных задач Автор: Корбу Наталья Александровна МОУ Средняя общеобразовательная школа №7 города Новокуйбышевска Самарской области.

Исторические сведения Основы теории графов как математической науки заложил в 1736 году Леонард Эйлер. Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок.

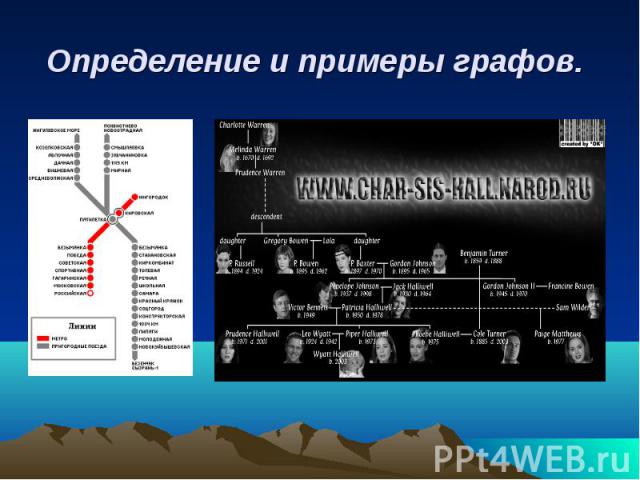
Определение и примеры графов.

Задачи о Кёнигсбергских мостах. Рассмотрим знаменитую задачу о Кёнигсбергских мостах. Бывший Кёнигсберг (сейчас это город Калининград) расположен на реке Прегель. В пределах города река омывает два острова.С берегов на острова были перекинуты мосты. Жители города предлагали туристам следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причём на каждом мосту нужно побывать только один раз.

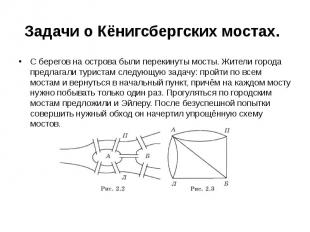
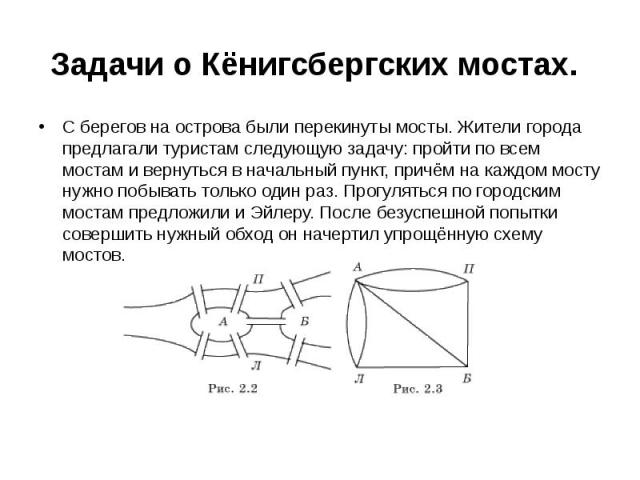
Задачи о Кёнигсбергских мостах. С берегов на острова были перекинуты мосты. Жители города предлагали туристам следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причём на каждом мосту нужно побывать только один раз. Прогуляться по городским мостам предложили и Эйлеру. После безуспешной попытки совершить нужный обход он начертил упрощённую схему мостов.

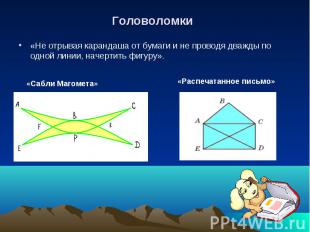
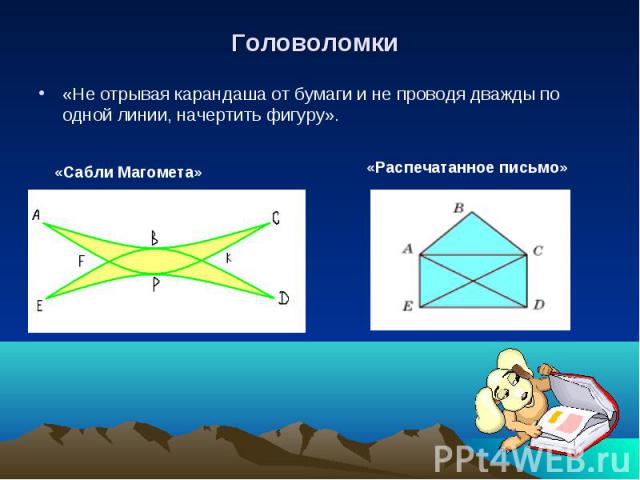
Головоломки «Не отрывая карандаша от бумаги и не проводя дважды по одной линии, начертить фигуру». «Сабли Магомета» «Распечатанное письмо»

Графы с цветными рёбрами. Перейдём к рассмотрению графов, в которых рёбра могут быть окрашены в несколько цветов. Такой граф называется графом с цветными рёбрами. Так же будем рассматривать такие графы, у которых каждая пара вершин соединена ребром. Такие графы называются полными. Применение графов с цветными рёбрами упрощает решение некоторых задач и делает их более наглядными.

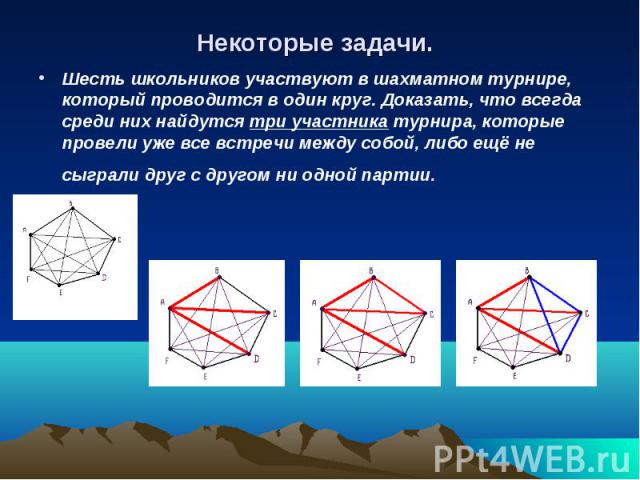
Некоторые задачи. Шесть школьников участвуют в шахматном турнире, который проводится в один круг. Доказать, что всегда среди них найдутся три участника турнира, которые провели уже все встречи между собой, либо ещё не сыграли друг с другом ни одной партии.

Некоторые задачи. 1) На географической карте выбраны пять городов. Известно, что из любых трёх из них найдутся два, соединённые авиалиниями, и два – не соединённые. Докажите, что: 1. Каждый город соединён авиалиниями с двумя и только с двумя другими городами. 2. Вылетев из любого города, можно облететь пять остальных городов, побывав в каждом по одному разу, и вернуться назад. 2) В офисе 15 компьютеров. Можно ли соединить их друг с другом так, чтобы каждый был соединен ровно с тремя другими?3) В государстве 100 городов. Из каждого города выходит четыре дороги. Сколько всего дорог в государстве?

Выводы В данной работе рассмотрены некоторые элементарные понятия и положения теории графов, которые применяются при решении головоломок и задач. Решение задач нестандартными приёмами, которые не изучаются в курсе средней школы, расширяют математический кругозор, пробуждают интерес к необычным разделам математики, учат находить нестандартные пути решения задач, особенно задач практической направленности.