Презентация на тему: Математические модели (7 класс)

Математические модели Выполнила презентациюучитель информатики МОУ «СОШ №20» Поспелова Г. В.г. Новомосковск Тульская область

§ 2.4. Математические модели Основным языком информационного моделирования в науке является язык математики. Модели, построенные с использованием математических понятий и формул, называются математическими моделями.Математическая модель - информационная модель, в которой параметры и зависимости между ними выражены в математической форме.

Например, известное уравнение S=vt, где S - расстояние, v - скорость t - время, представляет собой модель равномерного движения, выраженную в математической форме.

Рассматривая физическую систему: тело массой m, скатывающееся по наклонной плоскости с ускорением a под воздействием силы F, Ньютон получил соотношение F = mа. Это математическая модель физической системы.

Математическое моделирование Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятия числа, геометрической фигуры, уравнения, являются примерами математических моделей. К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить математическую модель).

При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на языке математики.Пример: нужно определить площадь поверхности стола. Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой. Из всех свойств стола выделили три: форма поверхности (прямоугольник) и длины двух сторон. Не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется. Предположив, что поверхность стола – прямоугольник, легко указать исходные данные и результат. Они связаны соотношением S=ab.

   Рассмотрим пример приведения решения конкретной задачи к математической модели. Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Даны некоторые предположения о формах сундука и окнах иллюминатора и исходные данные решения задачи. Предположения:Иллюминатор имеет форму круга. Сундук имеет форму прямоугольного параллелепипеда. Исходные данные: D - диаметр иллюминатора; x - длина сундука; y - ширина сундука; z - высота сундука. Конечный результат: Сообщение: можно или нельзя вытащить.

Системный анализ условия задачи выявил связи между размером иллюминатора и размерами сундука, учитывая их формы. Полученная в результате анализа информация отобразилась в формулах и соотношениях между ними, так возникла математическая модель.Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом:

Пример 1:Вычислить количество краски для покрытия пола в спортивном зале.   Для решения задачи нужно знать площадь пола. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.Пусть A – длина пола,   B  - ширина пола, S1  - площадь, которую можно покрыть содержимым одной банки, N – количество банок. Площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.

Пример 2:Через первую трубу бассейн наполняется за 30 часов, через вторую трубу – за 20 часов. За сколько часов бассейн наполнится через две трубы?Решение:Обозначим время заполнения бассейна через первую и вторую трубу А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t. Так как через первую трубу бассейн наполняется за А часов, то 1/А –часть бассейна, наполняемая первой трубой за 1 час; 1/В - часть бассейна, наполняемая второй трубой за 1 час.Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/А+1/В.Можно записать: (1/А+1/В)t=1. получили математическую модель, описывающую процесс наполнения бассейна из двух труб. Искомое время можно вычислить по формуле:

Пример 3:На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А со скоростью 50 км/ч.Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.За t часов мотоциклист проедет 50t км и будет находится от А на расстоянии 50t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой: S=50t + 20, где t>0.Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: было у Миши х марок; у Андрея 1,5х. Стало у Миши х-8, у Андрея 1,5х+8. По условию задачи 1,5х+8=2(х-8).

Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: было у Миши х марок; у Андрея 1,5х. Стало у Миши х-8, у Андрея 1,5х+8. По условию задачи 1,5х+8=2(х-8). Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: во втором цехе работают x человек, в первом – 4х, а в третьем - х+50. х+4х+х+50=470. Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: первое число х; второе х+2,5. По условию задачи х/5=(х+2,5)/4.

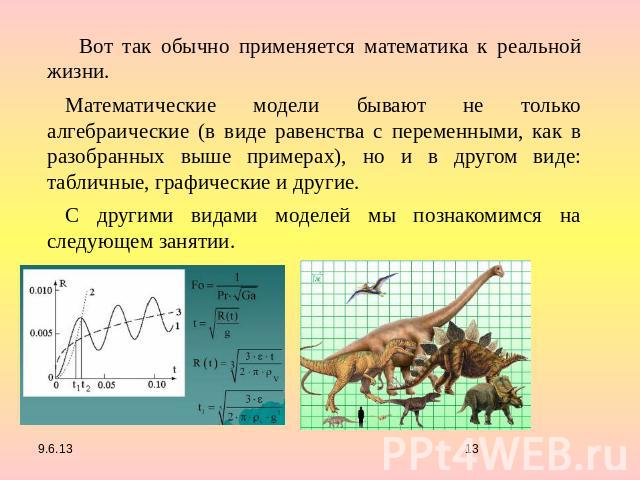
   Вот так обычно применяется математика к реальной жизни. Математические модели бывают не только алгебраические (в виде равенства с переменными, как в разобранных выше примерах), но и в другом виде: табличные, графические и другие.С другими видами моделей мы познакомимся на следующем занятии.

Задание на дом:§ 2.4 (стр. 54-58)№№ 1, 2, 3, 4 (стр. 57) в тетради

Спасибо за урок!

Источники Информатика и ИКТ : учебник для 7 классаАвтор : Босова Л. Л. Издательство : БИНОМ. Лаборатория знаний, 2009 Формат : 60x90/16 (в пер.), 229 с., ISBN : 978-5-9963-0092-1http://www.lit.msu.ru/ru/new/study (графики, схемы)http://images.yandex.ru (картинки)