Презентация на тему: Логические схемы

Таблицы истинности. Логические схемы Урок информатики. 10 класс. Устимкина Л.И., ББСОШ №1

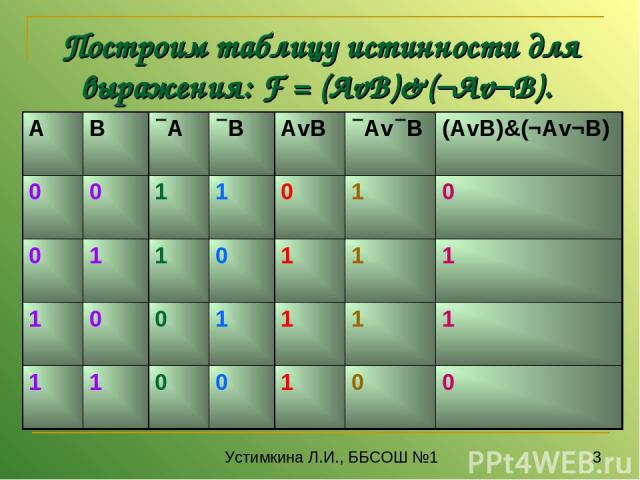
Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B). Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v,) = 7. Расставим порядок выполнения операций: 1 5 2 4 3 (A v B) & ( A v B) Устимкина Л.И., ББСОШ №1

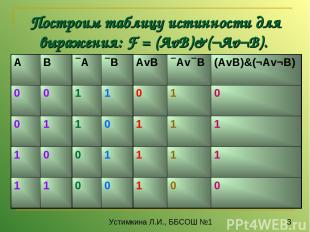
Построим таблицу истинности для выражения: F = (AvB)&(¬Av¬B). : Устимкина Л.И., ББСОШ №1

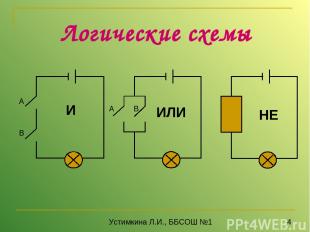
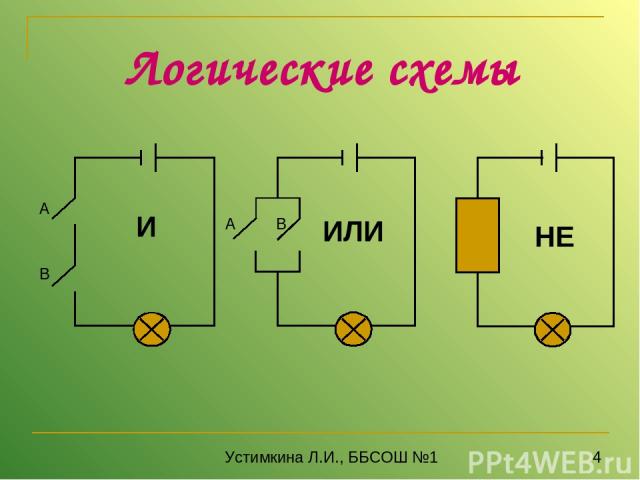
И ИЛИ НЕ Логические схемы Устимкина Л.И., ББСОШ №1

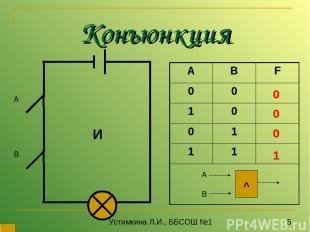
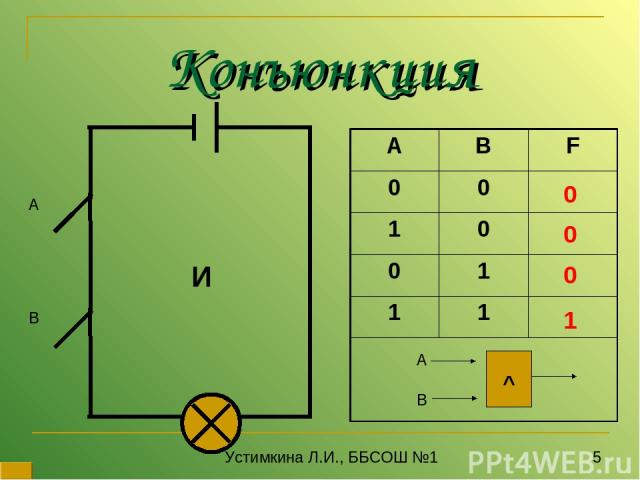
Конъюнкция А В 0 0 0 1 И Устимкина Л.И., ББСОШ №1

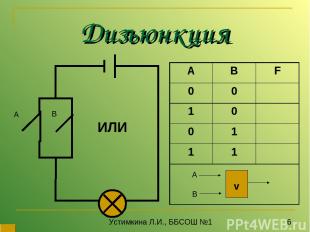
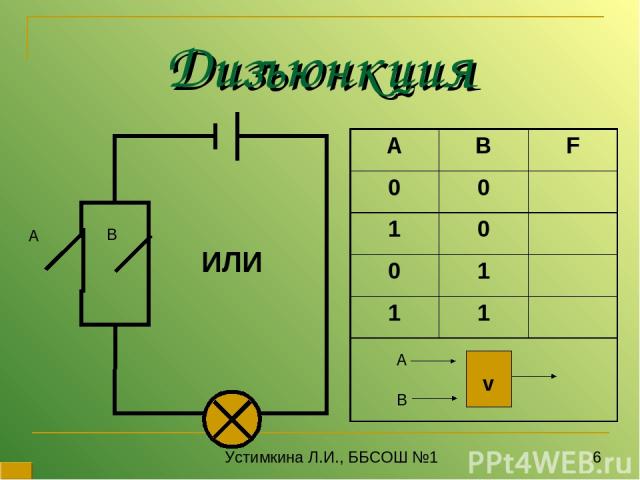
Дизъюнкция А В ИЛИ Устимкина Л.И., ББСОШ №1

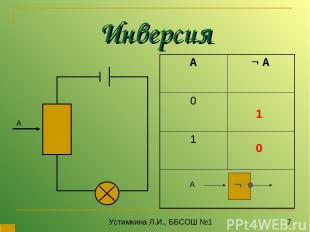
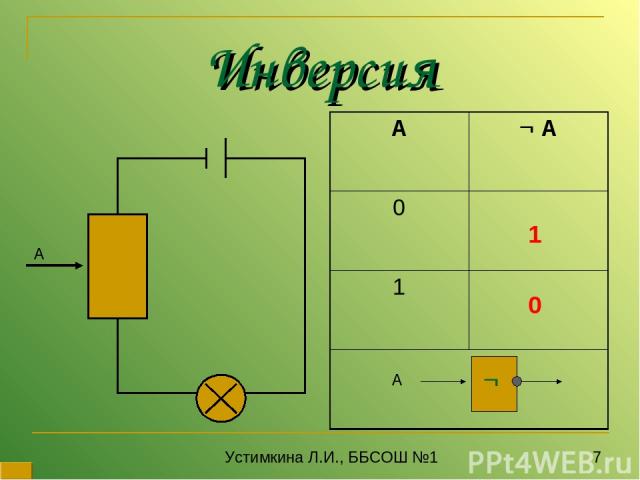
Инверсия А 1 0 Устимкина Л.И., ББСОШ №1

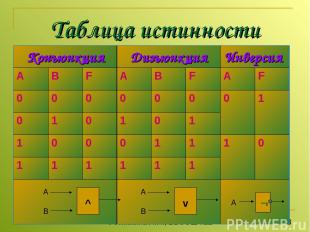
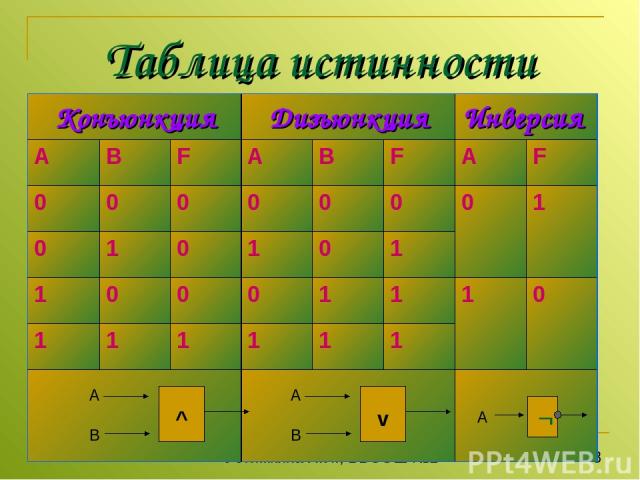
Таблица истинности Устимкина Л.И., ББСОШ №1

Построение логических схем Определить число логических переменных. Определить количество базовых логических операций и их порядок. Изобразить для каждой логической операции соответствующий вентиль. Соединить вентили в порядке выполнения логических операций. Устимкина Л.И., ББСОШ №1

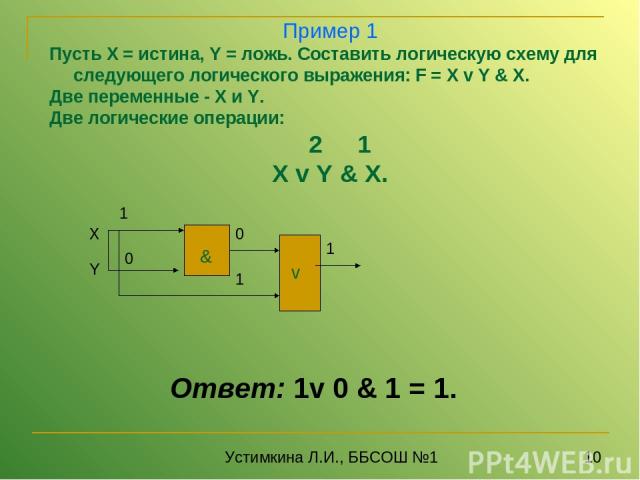
Х Y 1 0 0 1 1 Пример 1 Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X. Две переменные - X и Y. Две логические операции: 2 1 X v Y & X. Ответ: 1v 0 & 1 = 1. Устимкина Л.И., ББСОШ №1

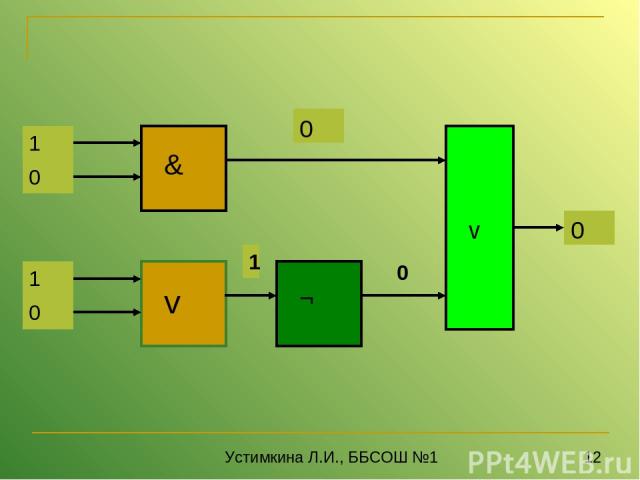
Пример 2 Постройте логическую схему, соответствующую логическому выраже нию F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0. Переменных две: X и Y; Логических операций четыре: конъюнкция, две дизъюнкции и инверсия: 1 4 3 2 X&Yv ¬ (YvX) Схему строим слева направо в соответствии с порядком логических операций Устимкина Л.И., ББСОШ №1

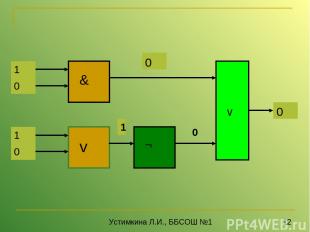
0 Устимкина Л.И., ББСОШ №1

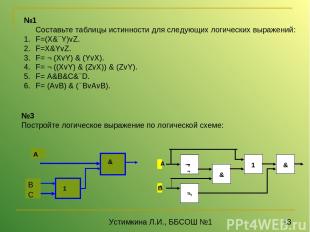
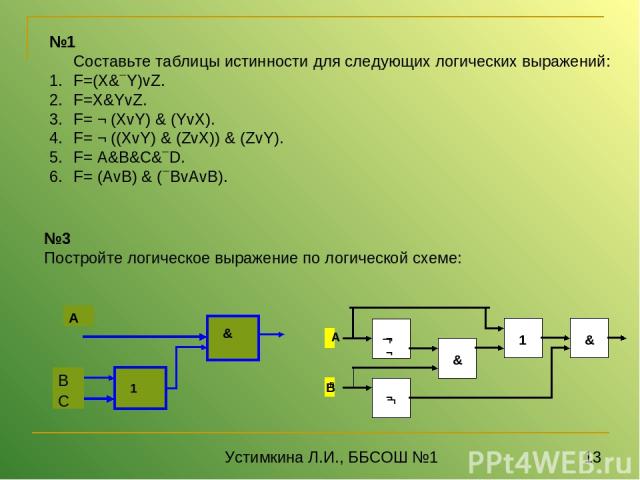
№1 Составьте таблицы истинности для следующих логических выражений: F=(X& Y)vZ. F=X&YvZ. F= ¬ (XvY) & (YvX). F= ¬ ((XvY) & (ZvX)) & (ZvY). F= A&B&C& D. F= (AvB) & ( BvAvB). №3 Постройте логическое выражение по логической схеме: А В ¬ ¬ Устимкина Л.И., ББСОШ №1

№4 Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения: F = AvB& C, если А = 1, В=1, С=1 (1). F = ¬ (AvB&C), если А=0, В=1, С=1 (1). F = AvB&C, если А=1, В=0, С=1 (0). F = (AvB) & (CvB), если А=0, В=1, С=0 (1). F = ¬ (А&В&С), если А=0, В=0, С=1 (1). F = ¬ (A&B&C) v (B & C v A), если А=1, В=1, С=0 (1). F = B& Av B&A, если А=0, В=0 (0). Устимкина Л.И., ББСОШ №1

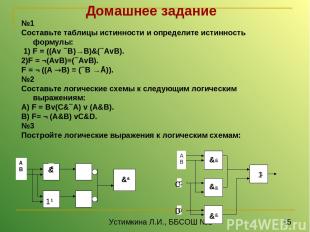
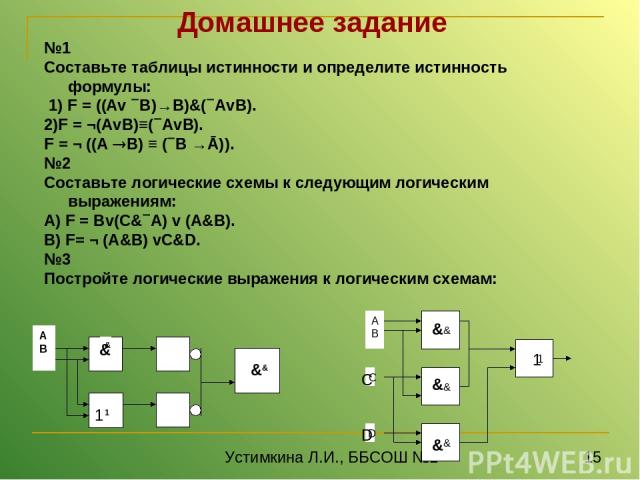
Домашнее задание №1 Составьте таблицы истинности и определите истинность формулы: 1) F = ((Av B)→B)&( AvB). 2)F = ¬(AvB)≡( AvB). F = ¬ ((А В) ≡ ( B →Ā)). №2 Составьте логические схемы к следующим логическим выражениям: A) F = Bv(C& A) v (A&B). B) F= ¬ (A&B) vC&D. №3 Постройте логические выражения к логическим схемам: C D & & 1 & & & 1 Устимкина Л.И., ББСОШ №1