Презентация на тему: Алгебра логики

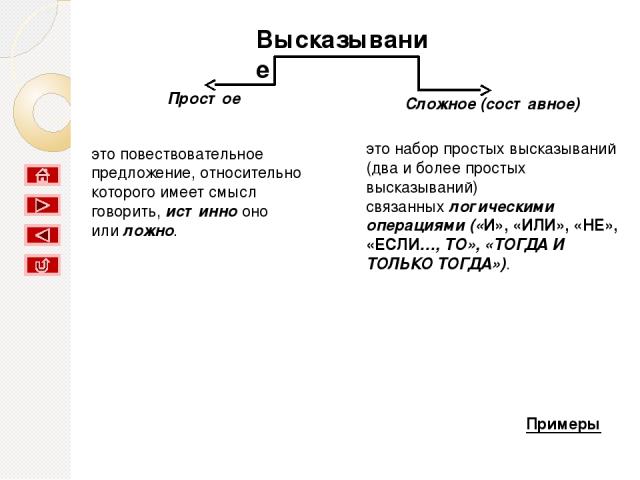
Алгебра логики рассматривает любое высказывание только с одной точки зрения — является ли оно истинным или ложным.   Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo. Например, предложение "6 — четное число." следует считать высказыванием, так как оно истинное. Предложение " Москва — столица Франции." тоже высказывание, так как оно ложное. не всякое предложение является логическим высказыванием. Но

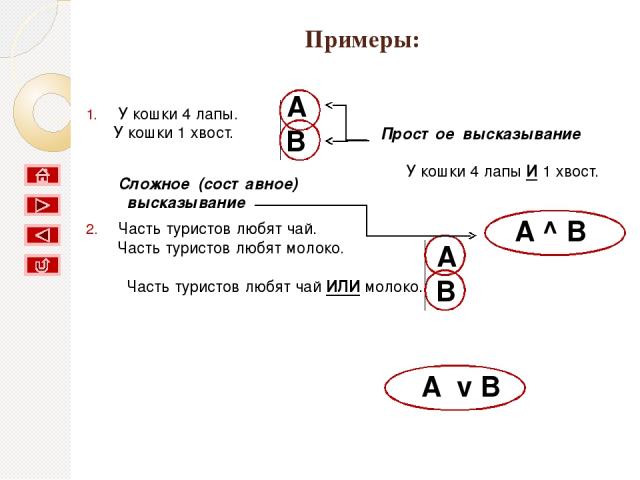
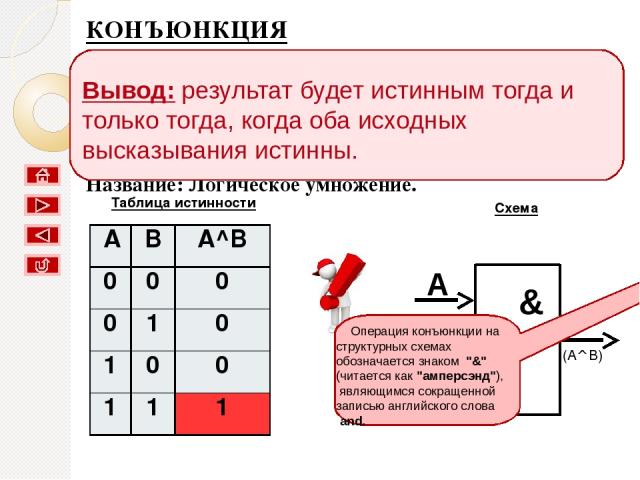
КОНЪЮНКЦИЯ Соответствует союзу И; Обозначение &; В языках программирования and; Название: Логическое умножение. Таблица истинности Схема A B F (A^B) & Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны. Операция конъюнкции на структурных схемах обозначается знаком  "&"  (читается как "амперсэнд"),  являющимся сокращенной записью английского слова  and. A B A^B 0 0 0 0 1 0 1 0 0 1 1 1

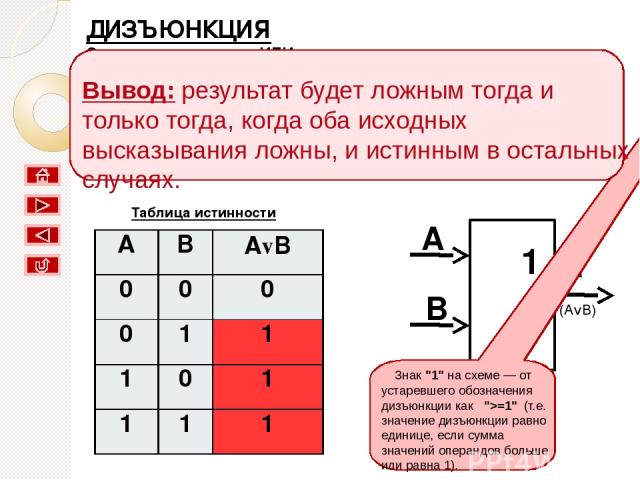
ДИЗЪЮНКЦИЯ Соответствует союзу ИЛИ; Обозначение V; В языках программирования or; Название: Логическое сложение. A B F (AvB) 1 Таблица истинности Знак "1" на схеме — от устаревшего обозначения дизъюнкции как   ">=1"  (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Вывод: результат будет ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным в остальных случаях. A B AvB 0 0 0 0 1 1 1 0 1 1 1 1

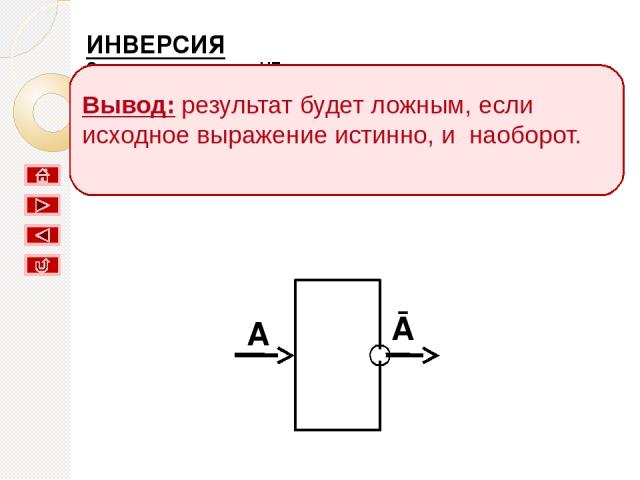
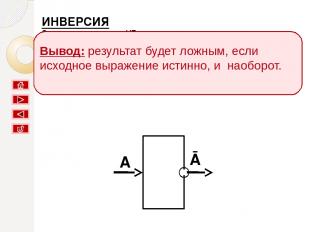
ИНВЕРСИЯ Соответствует союзу НЕ; Обозначение Ā; В языках программирования not; Название: Отрицание. A Ā Вывод: результат будет ложным, если исходное выражение истинно, и наоборот.

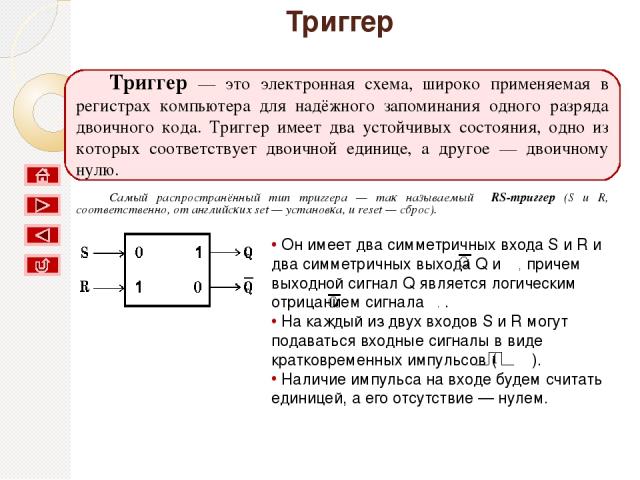
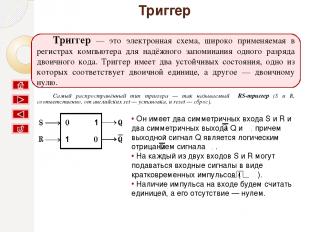
Триггер Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера: Он имеет два симметричных входа S и R и два симметричных выхода Q и , причем выходной сигнал Q является логическим отрицанием сигнала . . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( ). Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.

Высказываниями не являются, например, предложения "Ученик десятого класса." и "Информатика — интересный предмет.". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие "интересный предмет". Предложения типа "В городе A более миллиона жителей.", "У него голубые глаза." не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются  высказывательными формами.

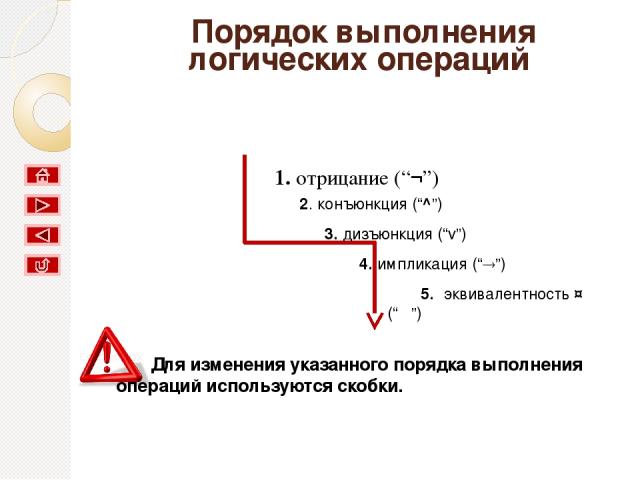
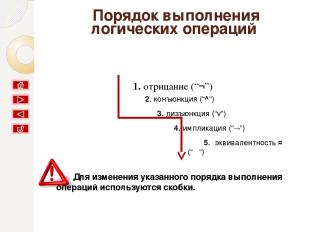
Порядок выполнения логических операций 1. отрицание (“¬”) ↔ 2. конъюнкция (“^”) 3. дизъюнкция (“v”) 4. импликация (“ ”) 5. эквивалентность (“ ”) Для изменения указанного порядка выполнения операций используются скобки.

Основные законы алгебры логики позволяют производить тождественные преобразования логических выражений:

Таблица истинности Таблица истинности - таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний. Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0), (0,1), (1,0), (1,1). Если формула содержит три переменные, то возможных наборов значений переменных восемь: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1). Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

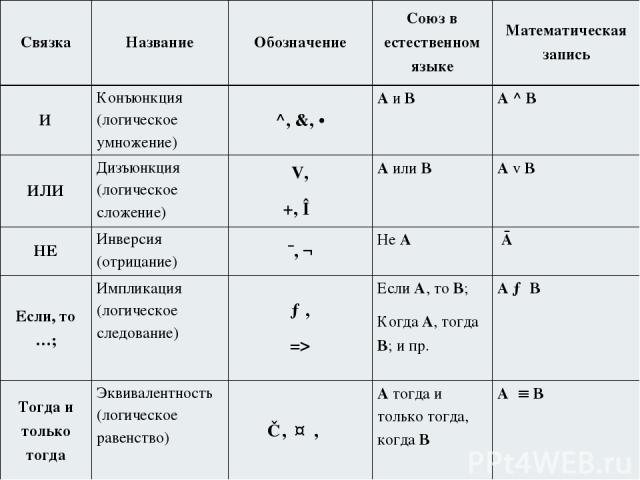
Основные логические связки

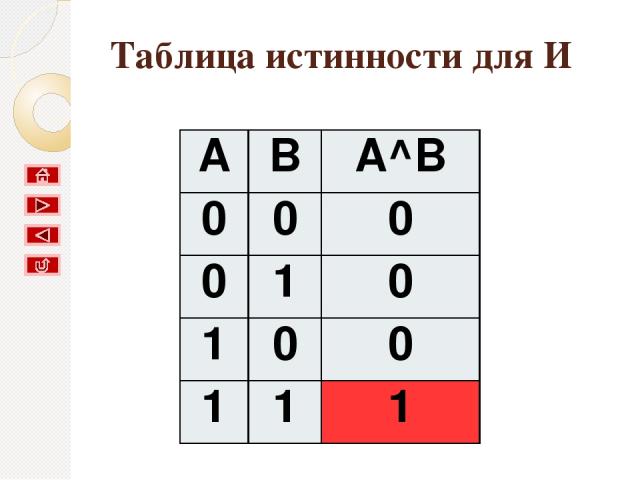
Таблица истинности для И A B A^B 0 0 0 0 1 0 1 0 0 1 1 1

Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны.

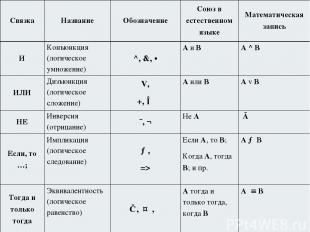
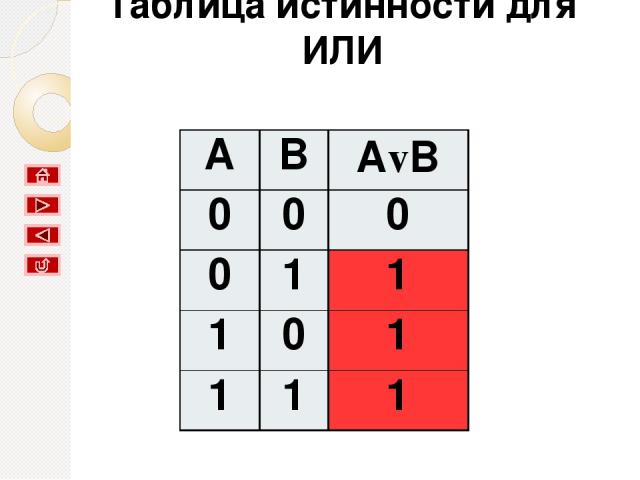
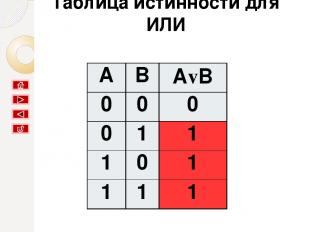
Таблица истинности для ИЛИ A B AvB 0 0 0 0 1 1 1 0 1 1 1 1

результат будет ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным в остальных случаях. Вывод:

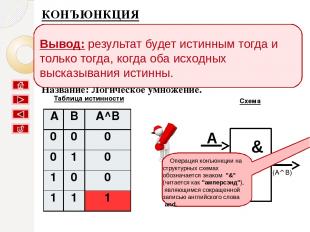
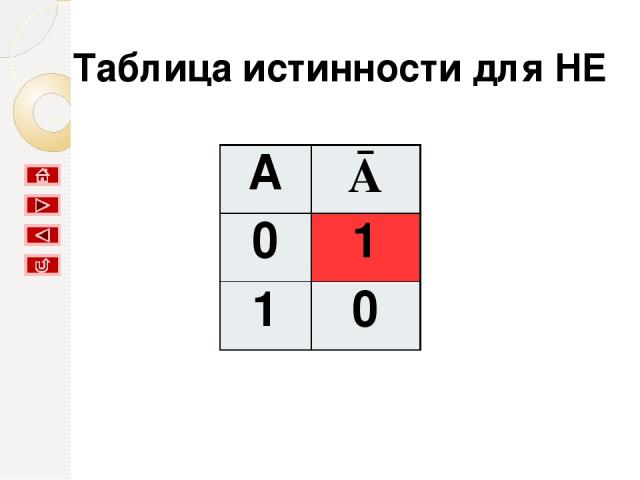
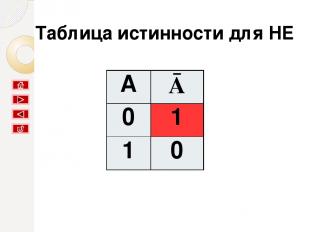
Таблица истинности для НЕ A Ā 0 1 1 0

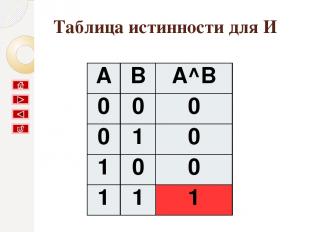
результат будет ложным, если исходное выражение истинно, и наоборот. Вывод:

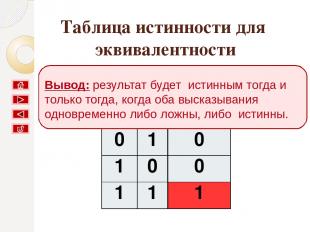
результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Вывод:

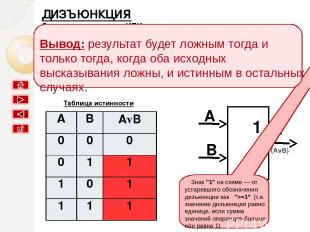
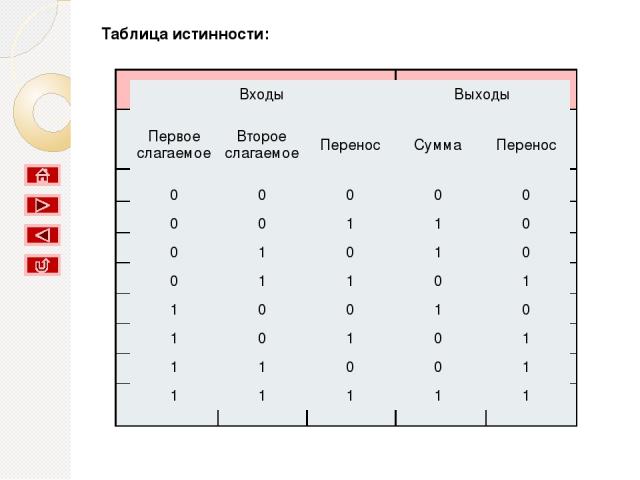
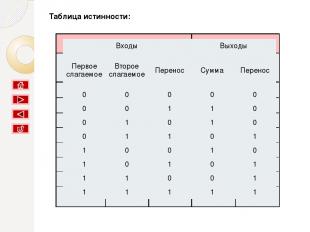
Таблица истинности: Входы Выходы Первое слагаемое Второе слагаемое Перенос Сумма Перенос 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1

Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы. Если  А и В — формулы,   то    Ā , А^В, АvВ ,   А → B ,   А≡В   —  формулы. Никаких других формул в алгебре логики нет. Определение логической формулы:

Тавтология Некоторые формулы принимают значение “истина” при любых значениях истинности входящих в них переменных. Например, формула А v Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

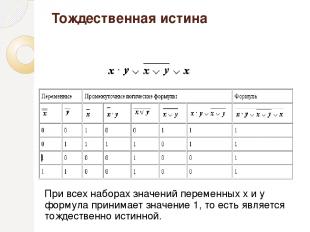
Тождественная истина При всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

Тождественная ложь В качестве другого примера рассмотрим формулу А • , которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати”. Очевидно, что эта формула ложна, так как либо А, либо обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Тождественная ложь При всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

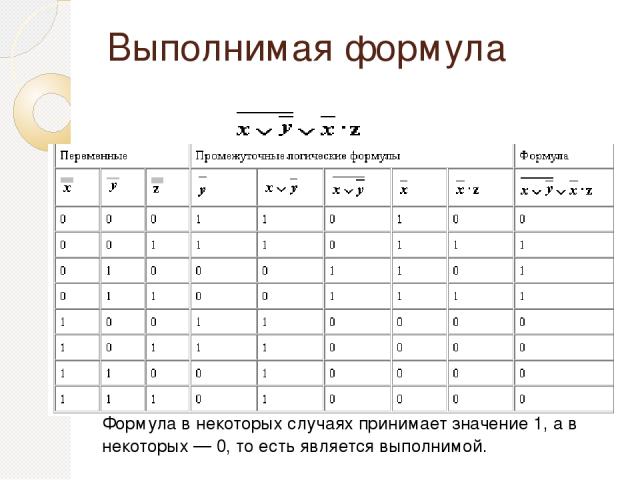
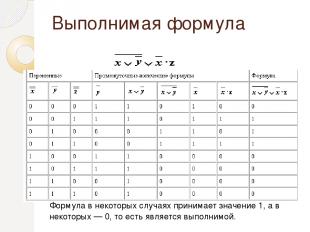
Выполнимая формула Формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

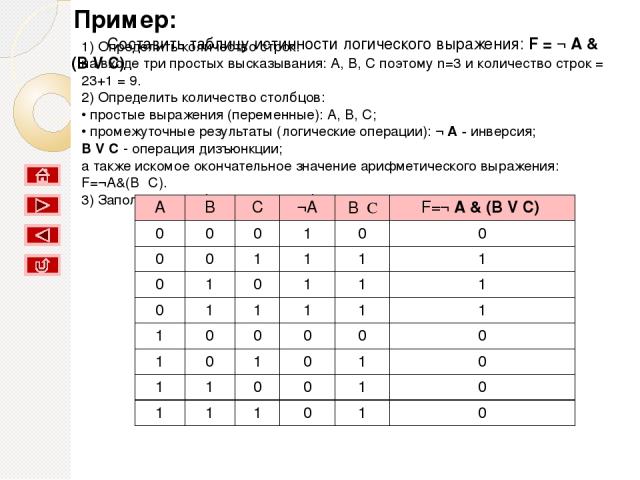
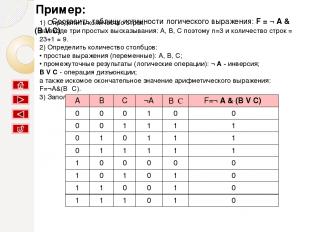
Как составлять таблицу истинности 1) Определить количество строк: количество строк = 2n + строка для заголовка, где n - количество простых высказываний. 2) Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; • определить количество переменных (простых выражений); • определить количество логических операций и последовательность их выполнения. 3) Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций. Пример

Основной источник: http://book.kbsu.ru/theory/index.html