Презентация на тему: Свойства и признаки равнобедренного треугольника

*

Девиз нашего урока : «Есть в математике нечто, вызывающее восторг» На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур. *

«Установка» : «Развивать и тренировать своё геометрическое зрение.» Кто ничего не замечает, Тот ничего не изучает. Кто ничего не изучает, Тот вечно хнычет и скучает. *

Треугольник – самая простая замкнутая геометрическая фигура, одна из первых, свойства которой человек узнал ещё в глубокой древности В одном египетском папирусе 4000-летней давности говорилось  о площади равнобедренного треугольника. Через 2000 лет в Древней Греции очень активно велось изучение его свойств. Император Франции Наполеон свободное время посвящал занятиям математикой и, в частности, изучению свойств треугольников. Большой вклад в исследование треугольников внес знаменитый математик …, имя которого мы назовём, ответив на следующие вопросы

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны ; *

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны ; *

Биссектриса треугольника – луч, делящий угол на два равных угла ; *

Отрезок биссектрисы угла, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника ; *

Медианы треугольника пересекаются в одной точке, и точка пересечения всегда лежит внутри треугольника ; *

Из точки, не лежащей на прямой, можно провести, по крайней мере, два перпендикуляра к ней ; *

Две прямые называются перпендикулярными, если при их пересечении образуется хотя бы один прямой угол *

Сумма углов треугольника равна двести градусов. ; *

Три стороны треугольника пересекаются в одной точке, и она всегда лежит внутри треугольника ; *

Три биссектрисы треугольника пересекаются в одной точке, и эта точка лежит внутри треугольника . *

Из дошедших до нас сочинений Евклида наиболее знамениты «Начала», состоящие из 15 книг. В 1-й книге изучаются свойства треугольников * Древнегреческий математик. Дата рождения: ок. 325 года до н.э. Научная сфера: математика Известен как: «Отец Геометрии»

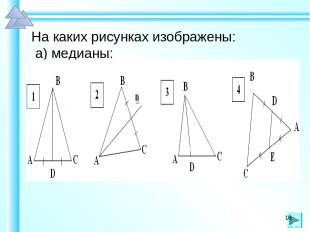
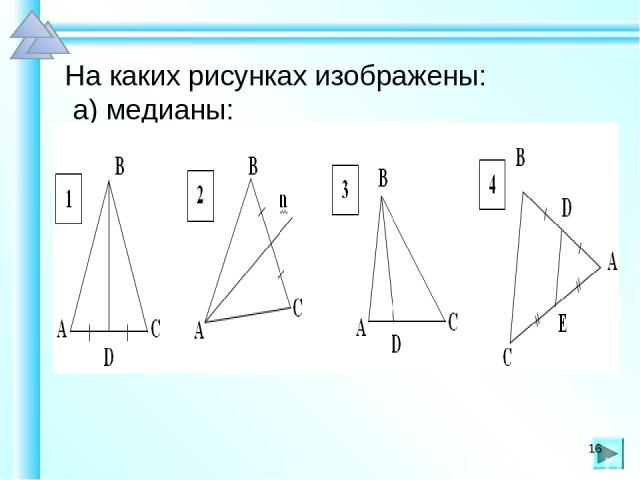
На каких рисунках изображены: а) медианы: *

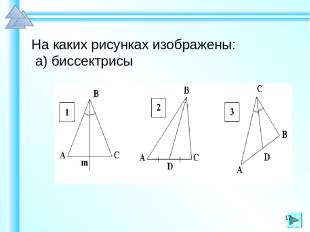
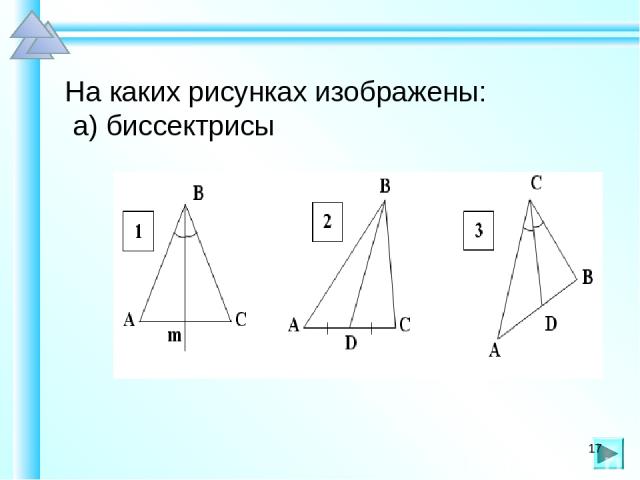
На каких рисунках изображены: а) биссектрисы *

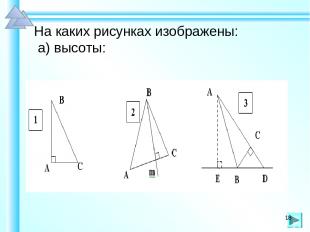
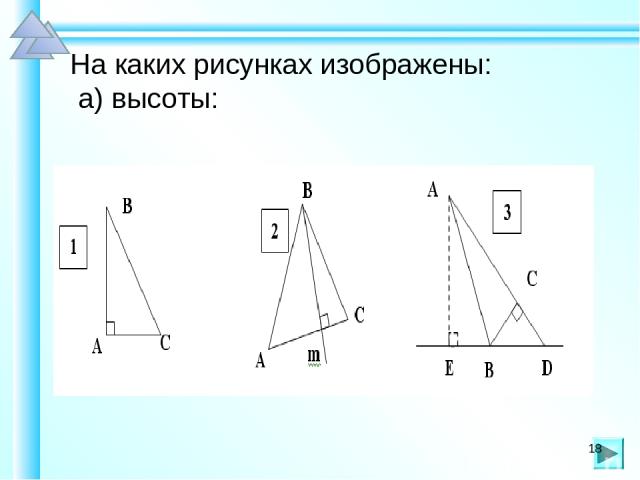
На каких рисунках изображены: а) высоты: *

5.12.12. Классная работа Равнобедренный треугольник. Свойства равнобедренного треугольника. *

Кто может растолковать понятие «свойство»? Что это такое? *

Свойство - характеристика, присущая вещам и явлениям, позволяющая отличать или отождествлять их. Каждому предмету присуще бесчисленное количество свойств, которые делятся на существенные и несущественные, необходимые и случайные, общие и специфические.. *

СВОЙСТВО — СВОЙСТВО, а, ср. Качество, признак, составляющий отличительную особенность кого чего н. … Толковый словарь Ожегова свойство — свойство особенность, присущая предмету и позволяющая включить его в тот или иной класс предметов. … Энциклопедический словарь I. СВОЙСТВО а; ср. кого чего. Существенный признак, качество, отличающее один предмет или одно лицо от другого; отличительная особенность, черта кого, чего либо. … Толковый словарь русского языка Кузнецова *

*

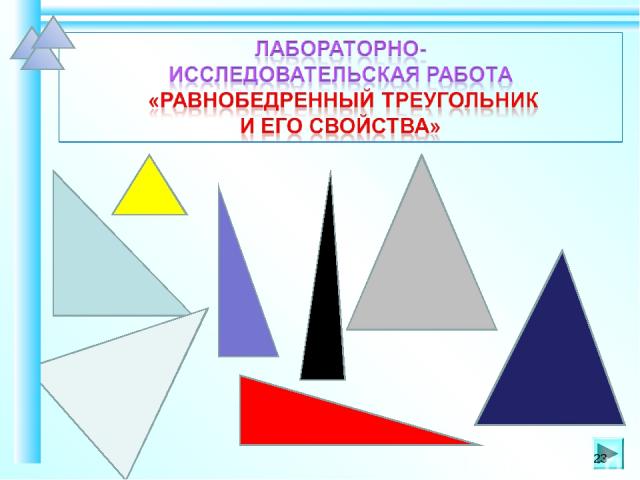
Цель: 1)Выяснить какие треугольники являются равнобедренными; 2)Какими свойствами они обладают. Оборудование: масштабная линейка, треугольник, транспортир, циркуль *

http://files.school-collection.edu.ru/dlrstore/7383a655-0dac-11dc-8314-0800200c9a66/index.htm http://files.school-collection.edu.ru/dlrstore/7383a654-0dac-11dc-8314-0800200c9a66/index.htm *

Ход работы: 1. Постройте два равнобедренных и один равносторонний треугольник, вырежьте их. 2.Методом сгибания исследуйте треугольники: найдите равные стороны и углы 3.Методом измерения исследуйте треугольники . 4Полученные результаты занести в таблицу. 5.Сделайте выводы. 6.Докажите свойства равнобедренного треугольника. *

Выводы: У равнобедренного треугольника боковые стороны равны. Не всякая биссектриса равнобедренного треугольника является медианой и высотой, а только та, которая проведена из вершины к основанию. Углы равнобедренного треугольника при основании равны. (Теоретически обосновали экспериментально полученные результаты )

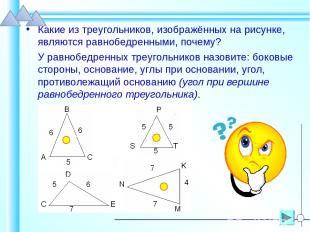
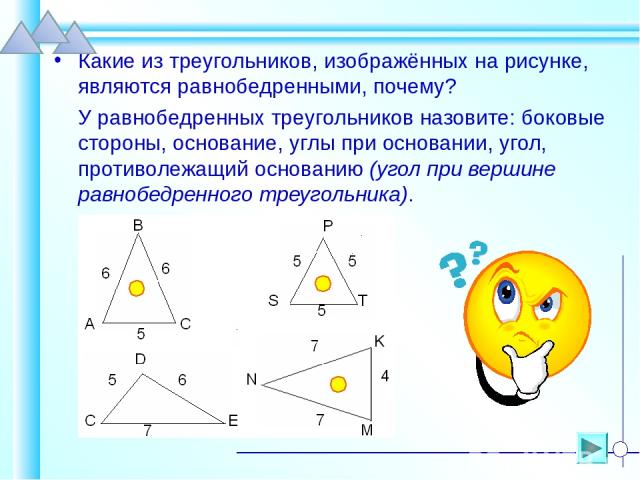
Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему? У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании, угол, противолежащий основанию (угол при вершине равнобедренного треугольника).

Решение задач В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника. В равнобедренном треугольнике основание равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника. В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника. В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

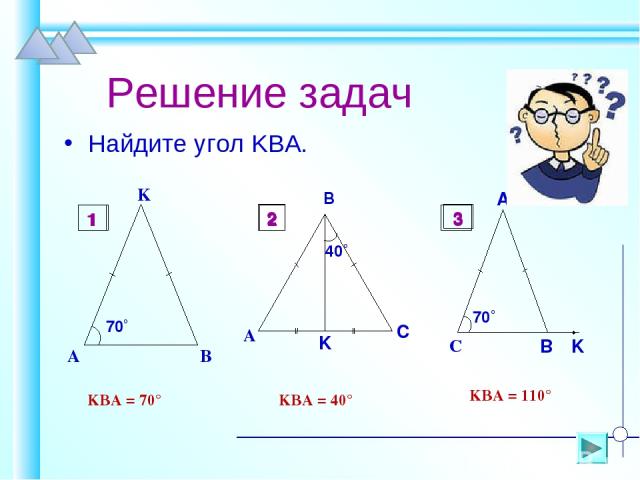
Решение задач Найдите угол KBA. ےKBA = 70° ےKBA = 40° ےKBA = 110° 1 2 3

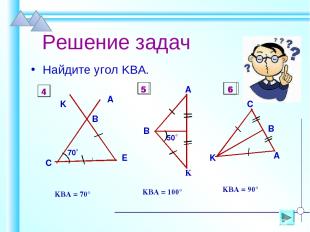
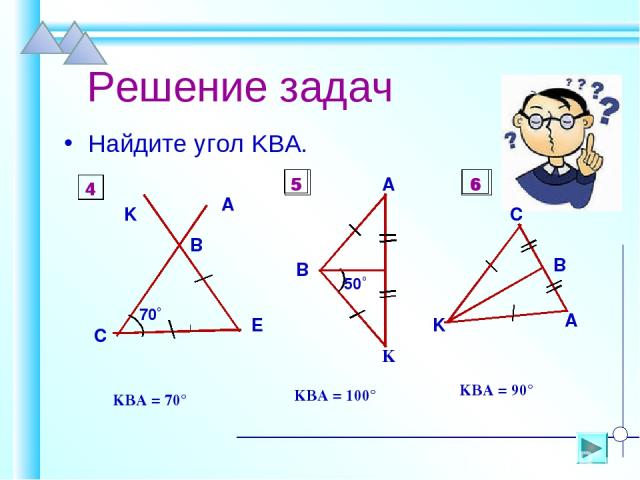
Решение задач Найдите угол KBA. ےKBA = 70° ےKBA = 100° ےKBA = 90° 4 5 6

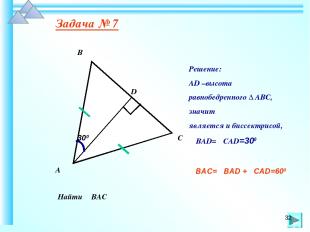
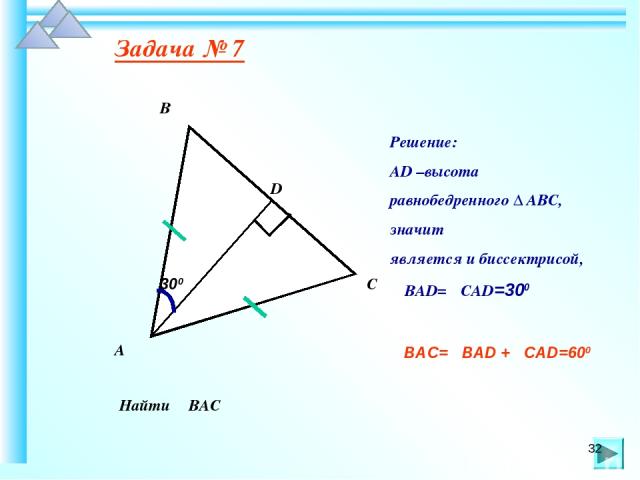
Задача № 7 Найти ∠ВАС 300 В А С D Решение: АD –высота равнобедренного ∆ АВС, значит является и биссектрисой, ∠ВАD=∠САD=300 ∠ВАС=∠ВАD +∠САD=600 *

* Достройте треугольник своего настроения

*