Презентация на тему: Определение и признак перпендикулярности плоскостей

Урок 3Определение и признак перпендикулярности плоскостей

Определение и признак параллельности прямой и плоскости Постройте плоскость, параллельную данной прямой и проходящую через а) заданную точку;б) другую данную прямую, Пусть а || b, а || α, b имеет с плоскостью α общую точку. Докажите, что прямая b лежит в плоскости α

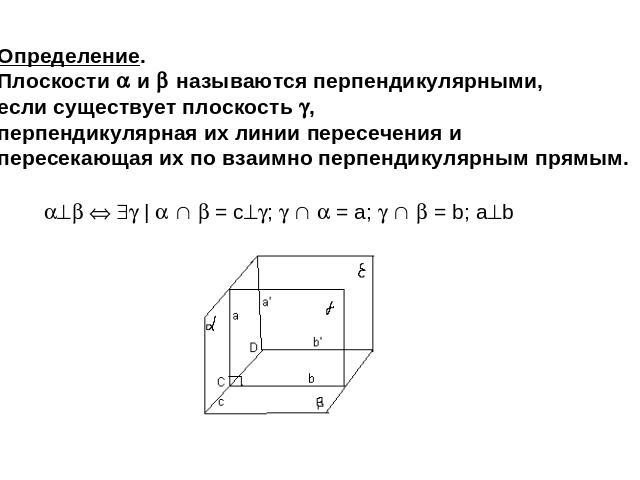
Определение. Плоскости и называются перпендикулярными, если существует плоскость , перпендикулярная их линии пересечения и пересекающая их по взаимно перпендикулярным прямым.

Сколько таких плоскостей существует? Что необходимо доказать, чтобы это определение было корректным? Докажем, что перпендикулярность и не зависит от выбора

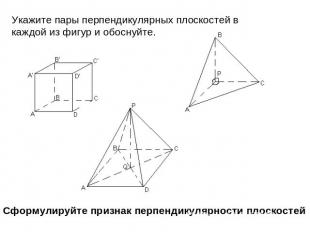
Укажите пары перпендикулярных плоскостей в каждой из фигур и обоснуйте.Сформулируйте признак перпендикулярности плоскостей

Теорема. Если плоскость содержит перпендикуляр к другой плоскости, то эти плоскости перпендикулярны Доказательство. Пусть а = A, тогда = c | Ac. 2) b | Ab и bc. 3) Так как а, то ас и аb. 4) | a и b, причем, с (признак перпендикулярности прямой и плоскости). Таким образом, (по определению).

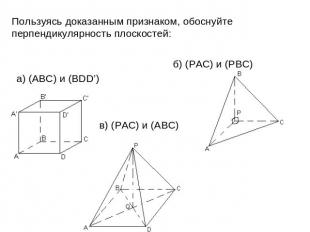
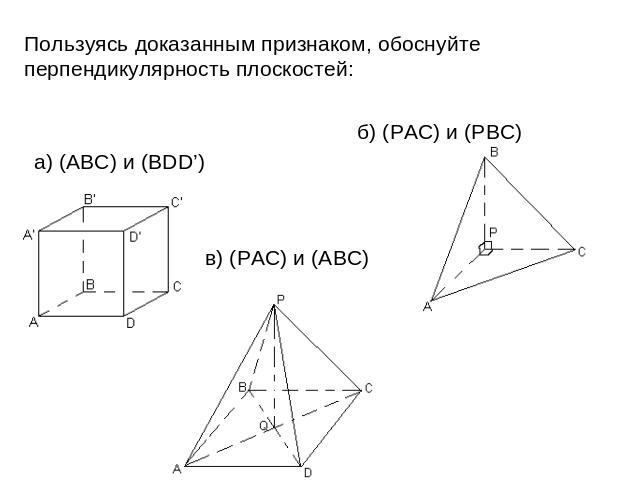
Пользуясь доказанным признаком, обоснуйте перпендикулярность плоскостей: