Презентация на тему: Конус

Конус Учитель математики А.А.Шарикова ГОКУ АО «Общеобразовательная школа при учреждениях исполнения наказаний»

История изучения геометрического тела конус С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки. В XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом. Евклид рассматривает  только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию. ЕВКЛИД (330-275гг. до н.э.)

Аполлоний Пергский- древнегреческий математик и астроном, ученик Евклида дал полное изложение теории и основанных им трудов «Конические сечения» в восьми книгах. У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса. АПОЛЛОНИЙ ПЕРГСКИЙ (260-170гг.до н. э.)

Строгое доказательство теорем, служащих для вывода формулы  объема конуса и изложенных в пяти предложениях 12 книги “Начал” Евклида, дал Евдокс Книдский. ЕВДОКС КНИДСКИЙ (408 - З55 гг.до.н.э )

Архимед древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики. В «Началах» Евклида мы находим определение только объёмов цилиндра и конуса, площадь же боковых поверхностей была найдена Архимедом. До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» он доказал следующую теорему: «Поверхность всякого равнобедренного (т.е. прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е. образующей) конуса и радиуса круга, являющегося основанием конуса».  АРХИМЕД (около 287 до н.э., Сиракузы,  Сицилия — 212 до н.э)

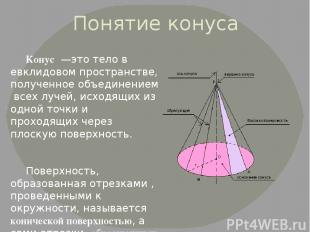
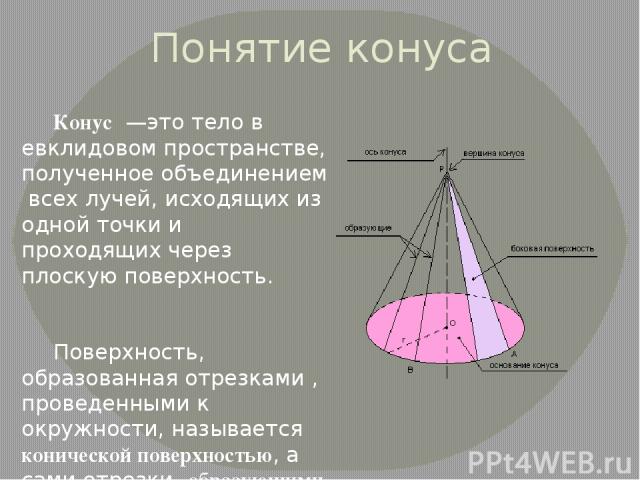
Понятие конуса Конус  —это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки и проходящих через плоскую поверхность. Поверхность, образованная отрезками , проведенными к окружности, называется конической поверхностью, а сами отрезки- образующими конической поверхности.

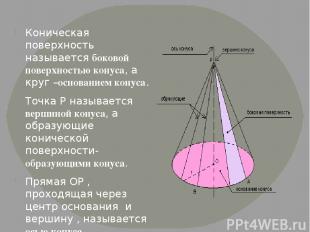
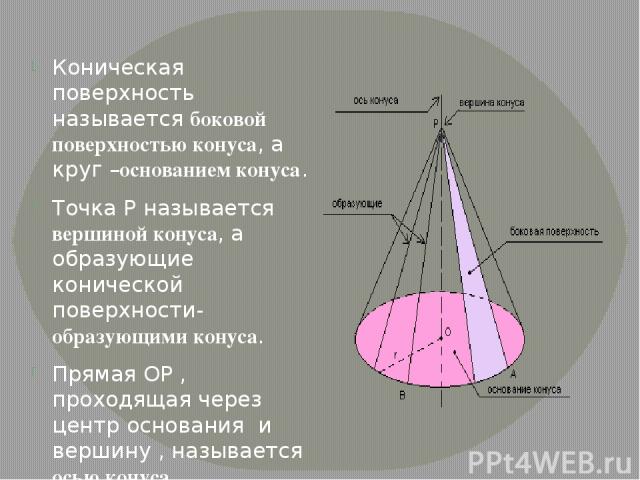
Коническая поверхность называется боковой поверхностью конуса, а круг –основанием конуса. Точка Р называется вершиной конуса, а образующие конической поверхности- образующими конуса. Прямая ОР , проходящая через центр основания и вершину , называется осью конуса. Отрезок ОР – высота конуса.

Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ.

Осевое сечение конуса Если секущая плоскость проходит через ось конуса, то сечение представляет собой авнобедренный треугольник, основание которого- диаметр основания конуса, а боковые стороны- образующие конуса. Это сечение - осевое.

Площадь поверхности конуса За площадь боковой поверхности конуса принимается площадь ее развертки. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания. Sбок. = П r l Sкон.= П r (l+r)

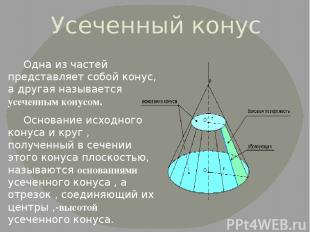
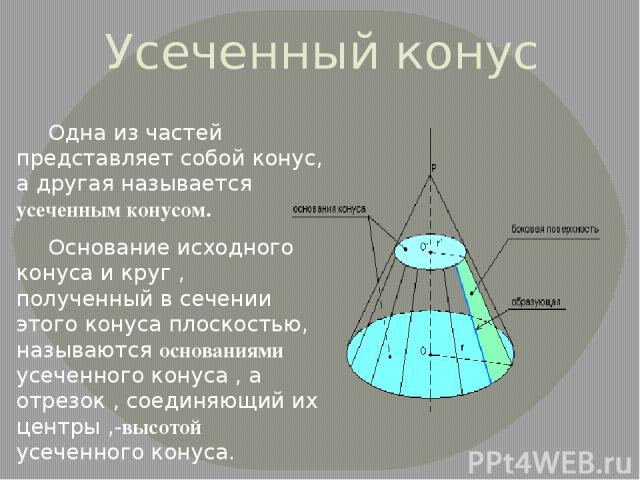
Усеченный конус Одна из частей представляет собой конус, а другая называется усеченным конусом. Основание исходного конуса и круг , полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса , а отрезок , соединяющий их центры ,-высотой усеченного конуса.

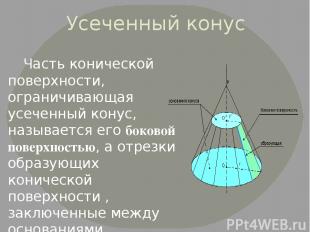
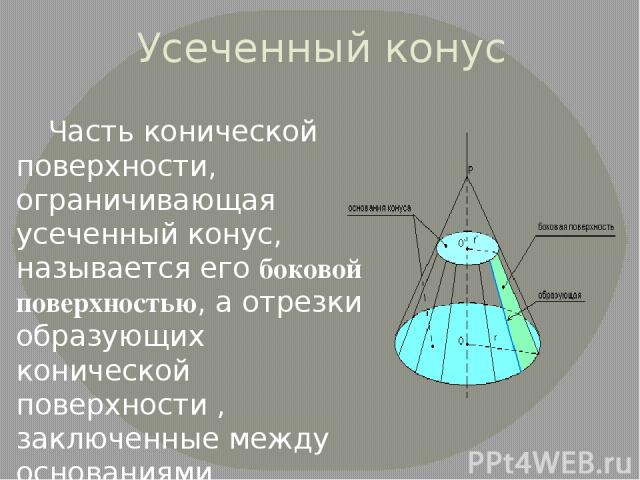
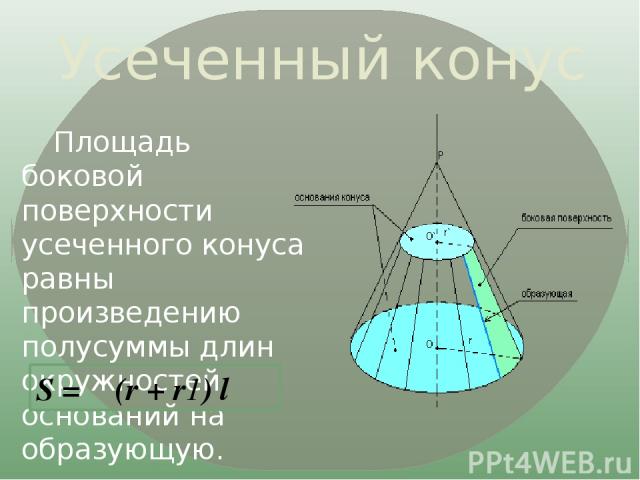
Усеченный конус Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности , заключенные между основаниями, называются образующими усеченного конуса.

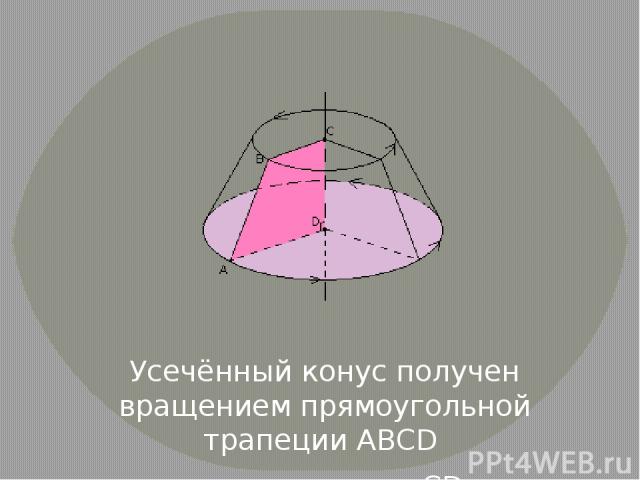
Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD.

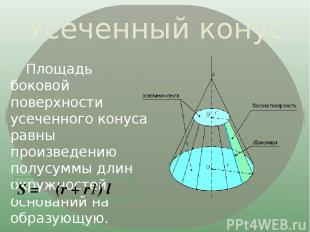
Усеченный конус Площадь боковой поверхности усеченного конуса равны произведению полусуммы длин окружностей оснований на образующую. S = π (r + r1) l