Презентация на тему: Проект «Полуправильные многогранники»

Проект на тему: Полуправильные многогранники Выполнила: Ильменская Наталья,10 кл.

Полуправильный многогранник -многогранник, у которого все его многогранные углы равны между собой (но не обязательно правильные), а все его грани- правильные многоугольники (но не все равны между собой).
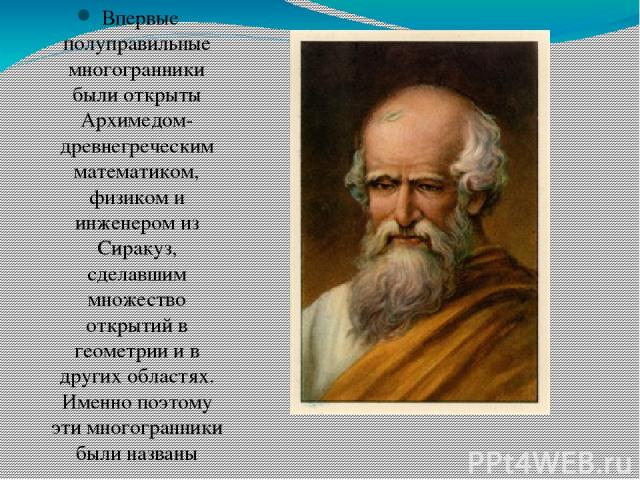
Впервые полуправильные многогранники были открыты Архимедом- древнегреческим математиком, физиком и инженером из Сиракуз, сделавшим множество открытий в геометрии и в других областях. Именно поэтому эти многогранники были названы Архимедовы тела.

Группы Архимедовых тел. Первую из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения. В нее входят: Усеченный куб. Усеченный октаэдр. Усеченный икосаэдр. Усеченный тетраэдр. Усеченный додекаэдр.

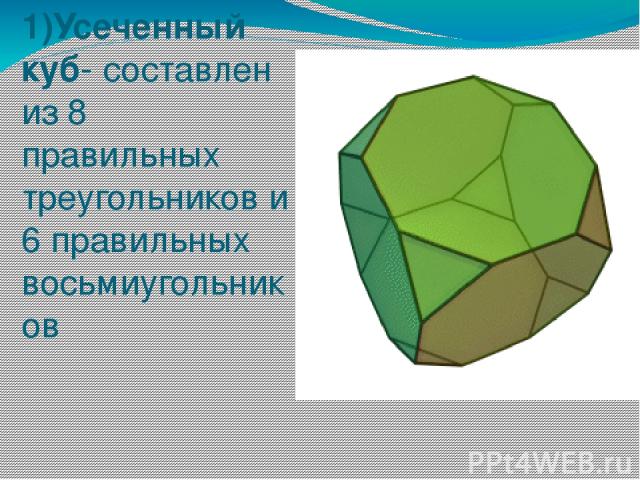
1)Усеченный куб- составлен из 8 правильных треугольников и 6 правильных восьмиугольников

2)Усеченный октаэдр- многогранник, составленный из 8 правильных шестиугольников и 6 квадратов.

3)Усеченный икосаэдр-многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников .
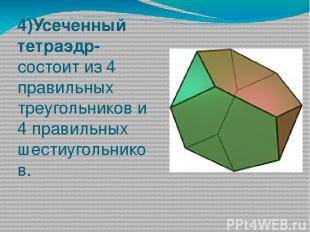
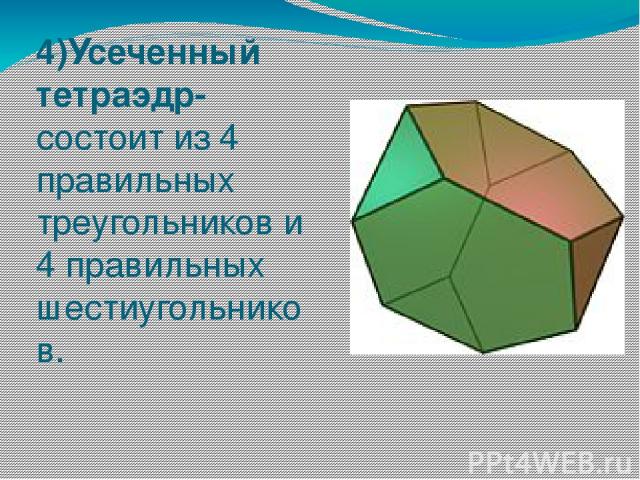
4)Усеченный тетраэдр- состоит из 4 правильных треугольников и 4 правильных шестиугольников.

5)Усеченный додекаэдр - состоит из 20 правильных треугольников и 12 десятиугольников.

Другую группу Архимедовых тел составляют два тела, именуемые квазиправильными многогранниками. В нее входят: 1. Кубооктаэдр. 2. Икосододекаэдр.

1)Кубооктаэдр- состоит из 8 правильных треугольников и 6 правильных квадратов.

2)Икосододекаэдр - состоит из 12 правильных пятиугольников 20 правильных треугольников.

В третью группу тел входят 2 многогранника, названия которых отличаются от названий предыдущей группы тем, что в них есть приставка « ромбо », соответственно ,их названия – 1.Ромбокубооктаэдр. 2.Ромбоикосододекаэдр.

1)Ромбокубооктаэдр- состоит из 18 квадратов и 8 правильных треугольников.

2)Ромбоикосододекаэдр- состоит из 12 правильных пятиугольников, 30 квадратов и 20 треугольников.

Четвёртую группу тел составляют многогранники, получившие названия “курносые” или “ плосконосые ”, такие забавные названия, даны многогранникам по той причине, что они получаются при последовательном срезании каждой из вершин. Это: 1.Курносый куб. 2.Курносый додекаэдр.

1)Курносый куб - состоит из 6 квадратов и 32 правильных треугольников.

2)Курносый додекаэдр - состоит из 12 пятиугольников и 80 правильных треугольников.

И пятая группа, самая малочисленная, состоит из одного многогранника- 1.Ромбокубооктаэдр.

1)Ромбокубооктаэдр- состоит из 18 квадратов и 8 правильных треугольников.

Полуправильные многогранники в жизни. Несомненно, в нашей повседневной жизни встречается множество полуправильных многогранников, и вот несколько примеров:

Форма книгохранилища — ромбокубооктаэдр. Библиотека — самый крупный из архитектурных ромбокубооктаэдров, возведенных в мире в настоящее время. Его высота составляет 73,6 м (23 этажа), а вес — 115 000 тонн. Национальная библиотека Беларуси.

Музей архитектуры Тойо на острове Омишима (Япония). В основе дизайна музея лежат геометрические фигуры: октаэдр, тетраэдр и Кубооктаэдр.

Здание Международного экономического комитета в Киеве Его купол конференц-зала своими гранями образует икосододекаэдр.

Полуправильные многогранники используются не только в архитектуре, но и в обычных вещах в повседневной жизни . К примеру:

Кресло Hedronics . В основе форм кресла лежит немного видоизмененный курносый куб.

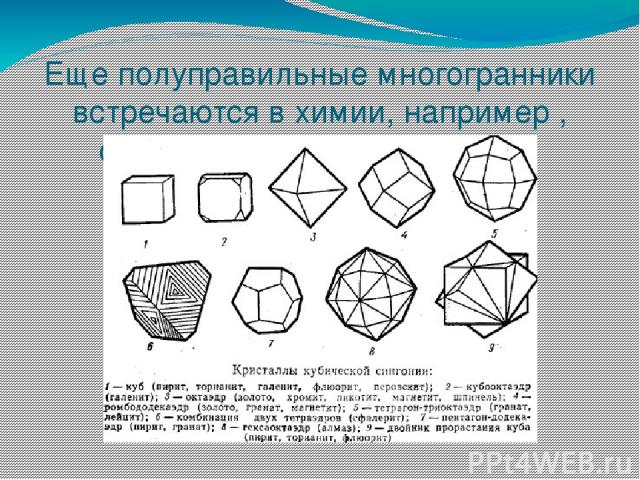
Еще полуправильные многогранники встречаются в химии, например , строение разных кристаллов.

Спасибо за внимание!!!