Презентация на тему: Геометрическое тело призма

Тема урока «Призма» Учитель математики МБОУ «Основная общеобразовательная Обуховская школа» Старооскольского городского округа Белгородской области Чепурных Любовь Ивановна 900igr.net

Цель урока: Закрепить полученные знания о призме и её элементов. Научиться применять теоретические знания к решению практических задач.

Эпиграф урока «Три пути ведут к знанию: путь РАЗМЫШЛЕНИЯ – это путь самый благородный, путь ПОДРАЖАНИЯ – это путь самый легкий и путь ОПЫТА – это путь самый горький». Конфуций

Пиши и говори правильно! (словарь математических терминов) Многогранник, параллелепипед, параллелограмм, призма, диагональ, высота, периметр, площадь, плоскость, поверхность.

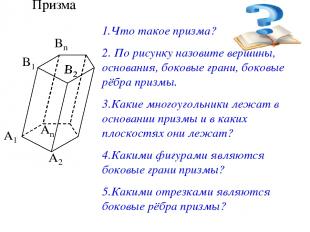
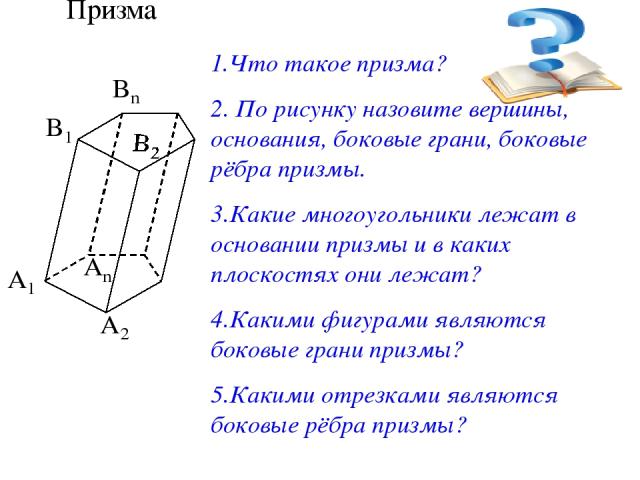
Призма 1.Что такое призма? 2. По рисунку назовите вершины, основания, боковые грани, боковые рёбра призмы. 3.Какие многоугольники лежат в основании призмы и в каких плоскостях они лежат? 4.Какими фигурами являются боковые грани призмы? 5.Какими отрезками являются боковые рёбра призмы?

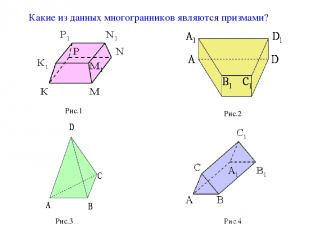
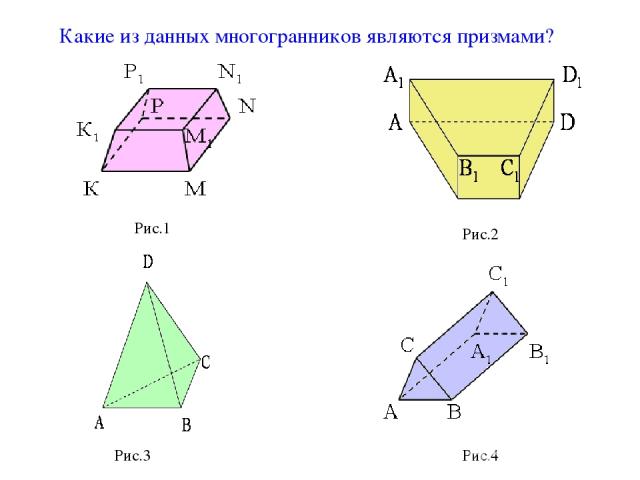
Рис.1 Рис.2 Рис.3 Рис.4 Какие из данных многогранников являются призмами?

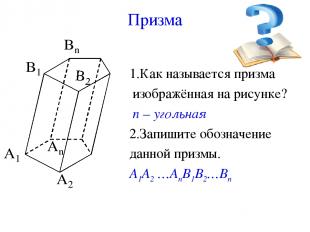
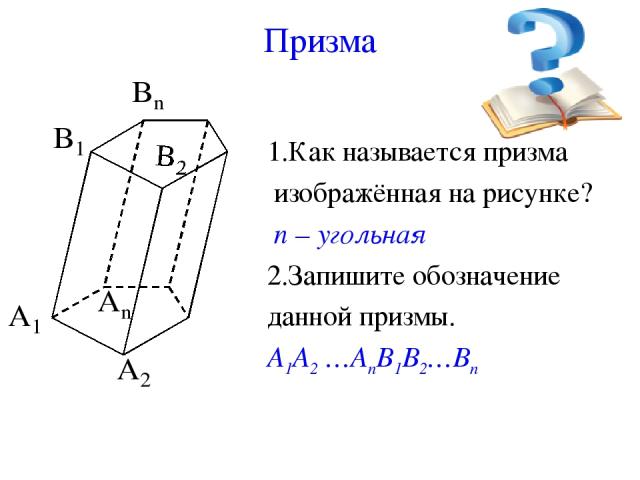
Призма 1.Как называется призма изображённая на рисунке? n – угольная 2.Запишите обозначение данной призмы. А1А2 …АnВ1В2…Вn

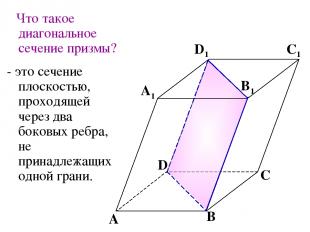
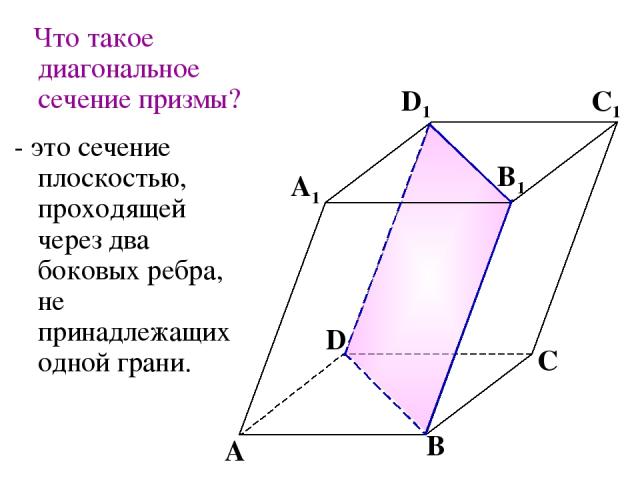
Что такое диагональное сечение призмы? - это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. A B C A1 D1 C1 B1 D

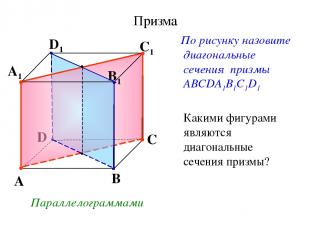
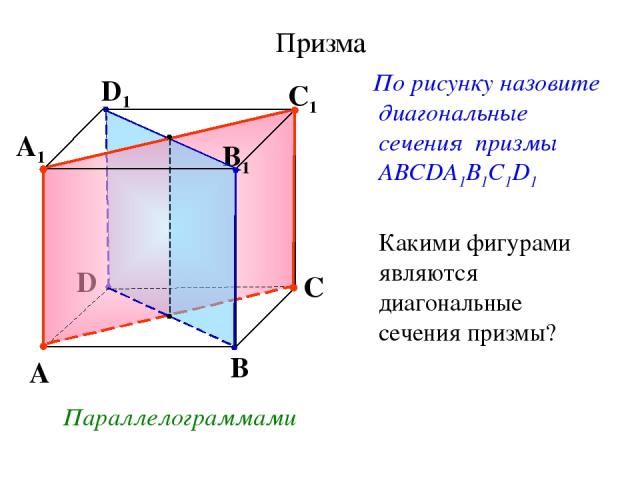
Призма По рисунку назовите диагональные сечения призмы АВСDА1В1С1D1 Какими фигурами являются диагональные сечения призмы? Параллелограммами D A B C A1 D1 C1 B1

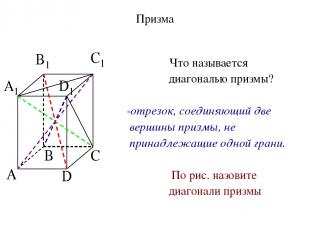
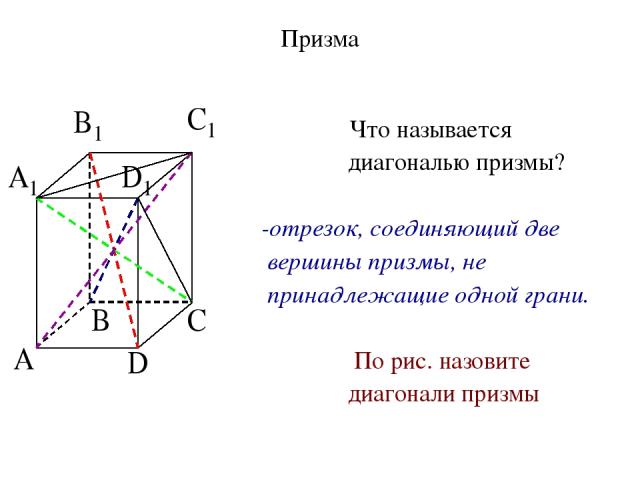
Призма Что называется диагональю призмы? -отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. По рис. назовите диагонали призмы

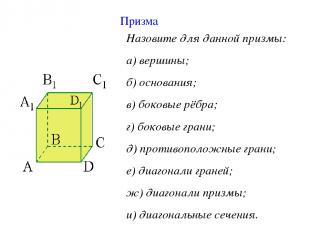
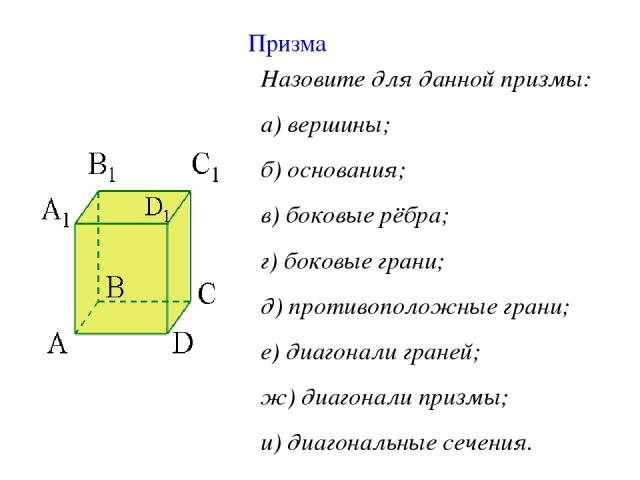
Призма Назовите для данной призмы: а) вершины; б) основания; в) боковые рёбра; г) боковые грани; д) противоположные грани; е) диагонали граней; ж) диагонали призмы; и) диагональные сечения.

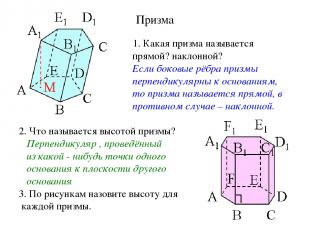
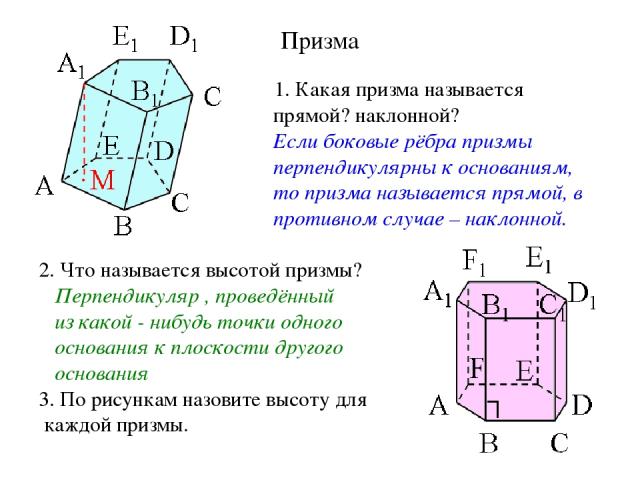
Призма 1. Какая призма называется прямой? наклонной? Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. 2. Что называется высотой призмы? Перпендикуляр , проведённый из какой - нибудь точки одного основания к плоскости другого основания 3. По рисункам назовите высоту для каждой призмы.

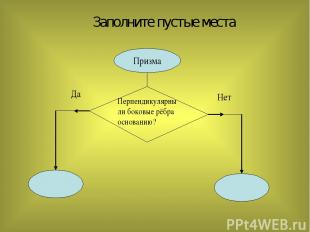
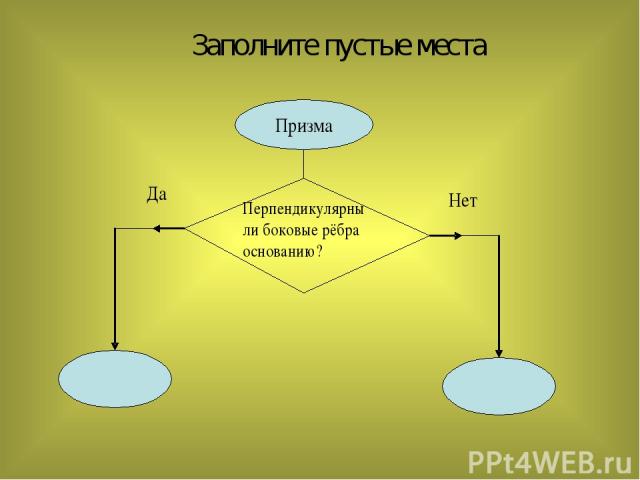
Заполните пустые места

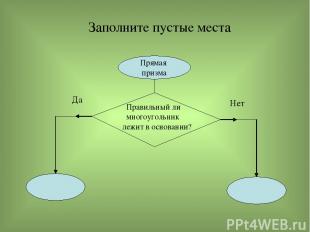
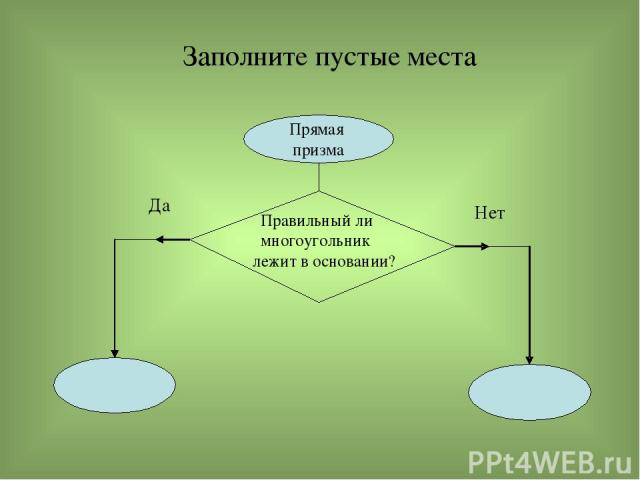
Заполните пустые места

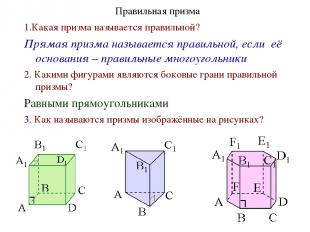
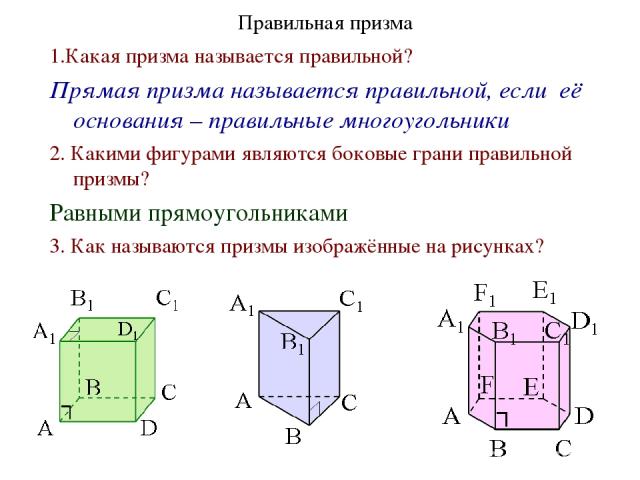
Правильная призма 1.Какая призма называется правильной? Прямая призма называется правильной, если её основания – правильные многоугольники 2. Какими фигурами являются боковые грани правильной призмы? Равными прямоугольниками 3. Как называются призмы изображённые на рисунках?

у = х2 > x2 + у2 = 1 2 ∙ 2 =?

Закончите предложения: Если основание призмы параллелограмм, то она называется параллелепипедом. 2. У параллелепипеда все грани - параллелограммы. У параллелепипеда противолежащие грани параллельны и равны. 4. Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.

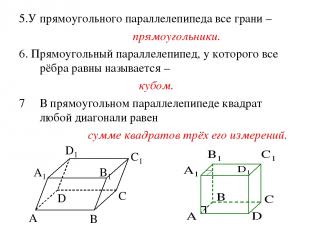
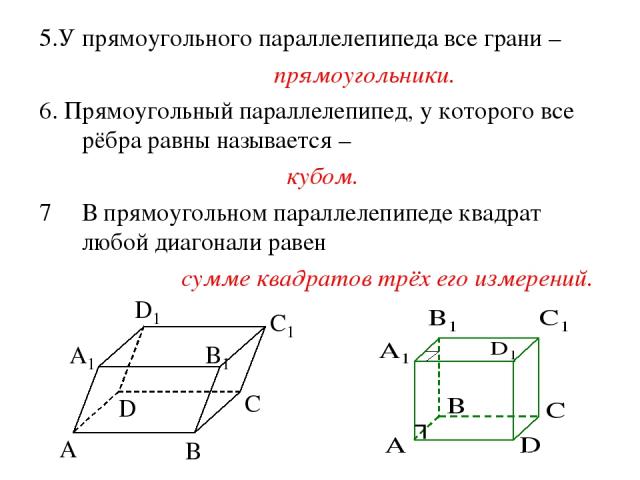
5.У прямоугольного параллелепипеда все грани – прямоугольники. 6. Прямоугольный параллелепипед, у которого все рёбра равны называется – кубом. В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений.

Площадью полной поверхности призмы называется сумма площадей всех её граней. Формула площади полной поверхности призмы: Sполн = Sбок + 2Sосн

Площадью боковой поверхности призмы называется сумма площадей её боковых граней. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. Формула площади боковой поверхности прямой призмы Sбок = Р h

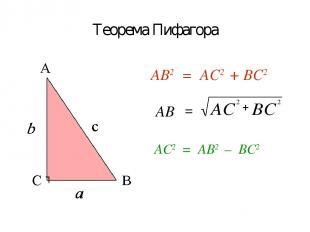
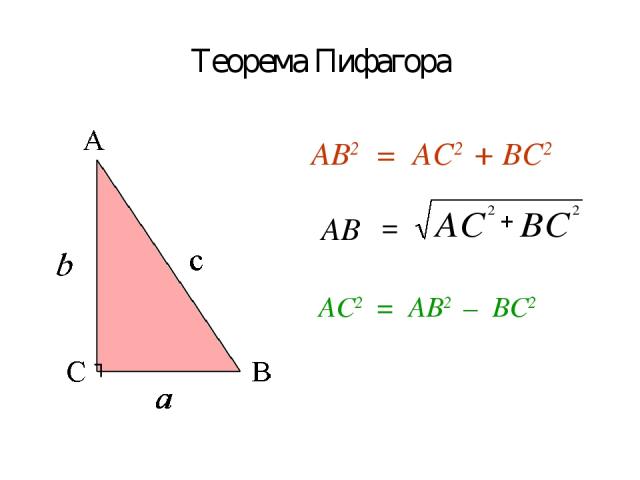
Теорема Пифагора АВ2 = АС2 + ВС2 ┐ АВ = АС2 = АВ2 – ВС2

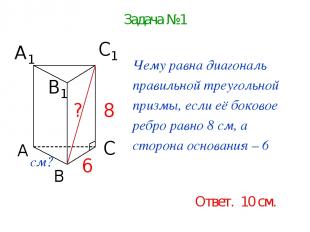
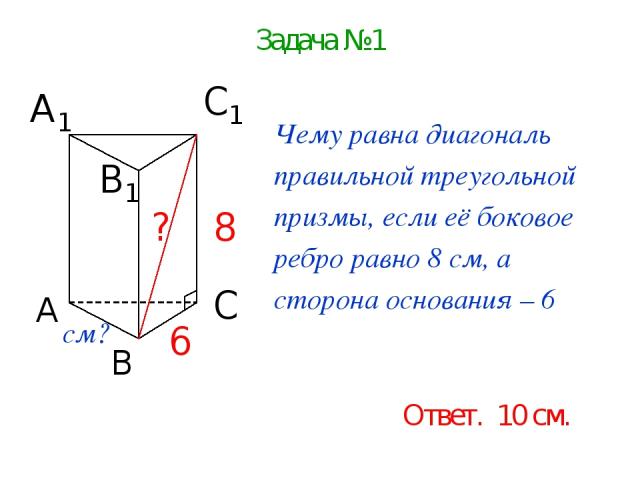
Задача №1 Чему равна диагональ правильной треугольной призмы, если её боковое ребро равно 8 см, а сторона основания – 6 см? Ответ. 10 см.

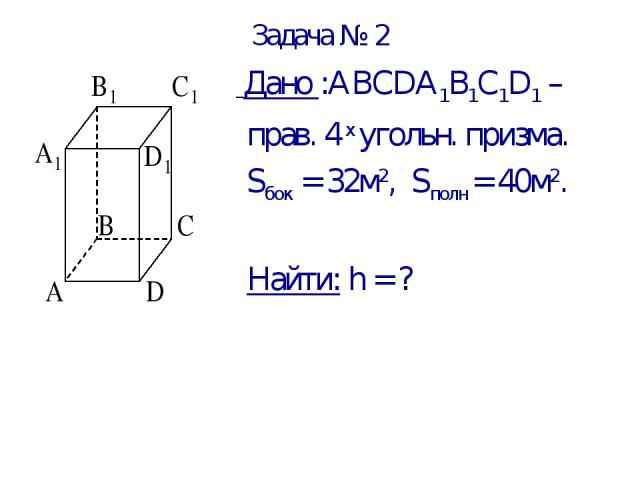
Задача № 2 Боковая поверхность правильной четырёхугольной призмы 32 м2, а полная поверхность 40 м2. Найдите высоту призмы.

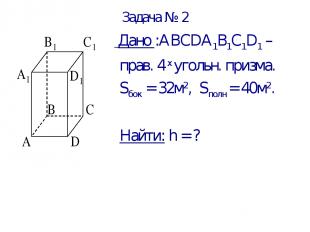
Задача № 2 Дано :АВСDА1В1С1D1 – прав. 4 х угольн. призма. Sбок = 32м2, Sполн = 40м2. Найти: h = ?

Задача № 2 Решение: Sбок прав. = Р∙h ; Sполн.= Sбок+2Sосн ; 2Sосн = Sполн – Sбок; Sосн =( Sполн- Sбок):2; Sосн =( 40 – 32) =4 м2 Sосн = АD2; => АD =2 м.; Р = 4∙АD = 4∙2 = 8 м.; Ответ. 4м. ;

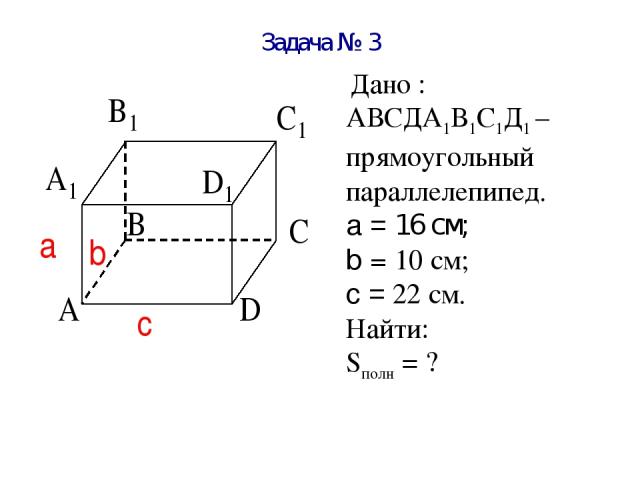
Задача № 3 Найдите полную поверхность прямоугольного параллелепипеда по трём его измерениям 10 см; 22 см; и 16 см.

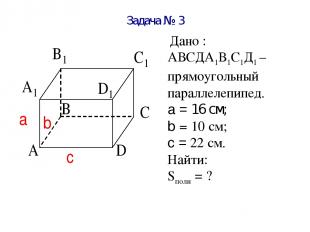
Задача № 3 Дано : АВСДА1В1С1Д1 – прямоугольный параллелепипед. a = 16 см; b = 10 см; c = 22 см. Найти: Sполн = ?

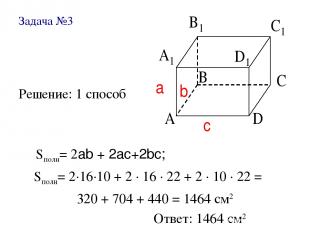
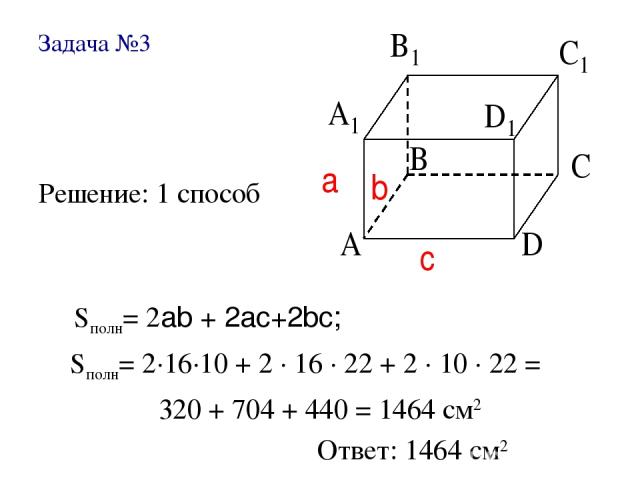
Задача №3 Решение: 1 способ Sполн= 2ab + 2ac+2bc; Sполн= 2∙16∙10 + 2 ∙ 16 ∙ 22 + 2 ∙ 10 ∙ 22 = 320 + 704 + 440 = 1464 см2 Ответ: 1464 см2

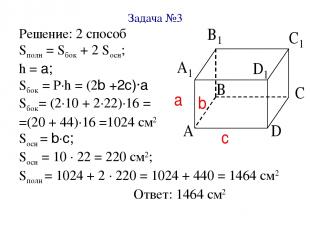
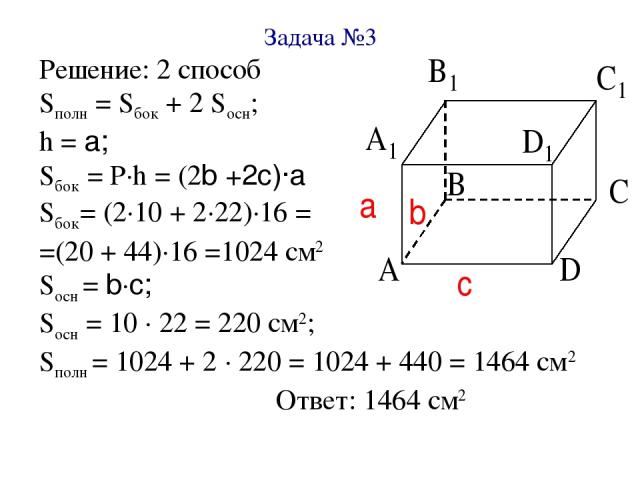
Задача №3 Решение: 2 способ Sполн = Sбок + 2 Sосн; h = a; Sбок = Р∙h = (2b +2c)∙a Sбок= (2∙10 + 2∙22)∙16 = =(20 + 44)∙16 =1024 см2 Sосн = b∙c; Sосн = 10 ∙ 22 = 220 см2; Sполн = 1024 + 2 ∙ 220 = 1024 + 440 = 1464 см2 Ответ: 1464 см2

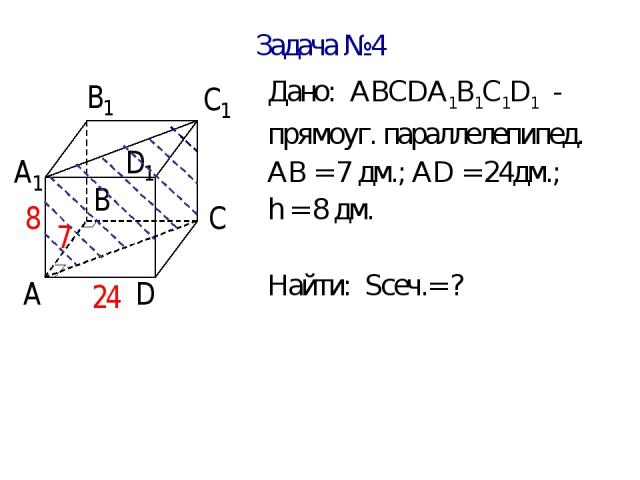
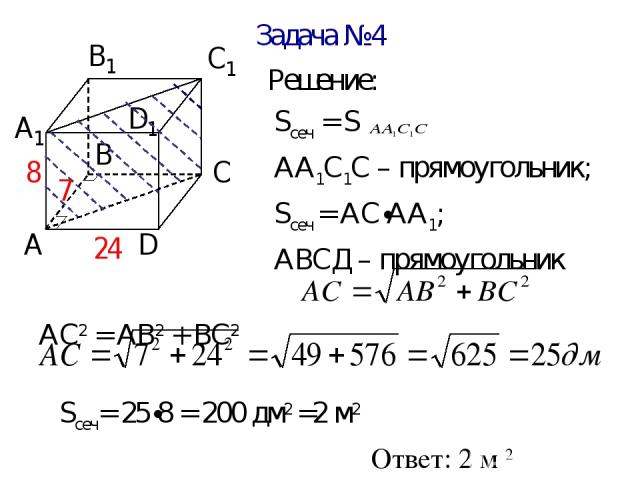
Задача №4 В прямоугольном параллелепипеде сторона основания 7 дм и 24 дм, а высота параллелепипеда 8 дм. Найдите площадь диагонального сечения. Ответ выразите в метрах.

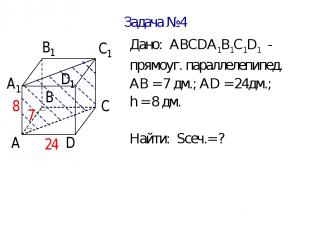
Задача №4 Дано: АВСDА1В1С1D1 - прямоуг. параллелепипед. АВ = 7 дм.; АD = 24дм.; h = 8 дм. Найти: Sсеч.= ?

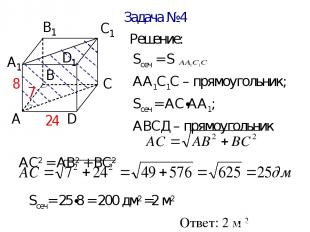
Задача №4 Решение: Sсеч = S АА1С1С – прямоугольник; Sсеч = АС∙АА1; АВСД – прямоугольник АС2 = АВ2 + ВС2 Sсеч= 25∙8 = 200 дм2 =2 м2 Ответ: 2 м 2

Домашнее задание на следующем слайде

Проект « Парник для теплицы» Теплице необходимо построить новые парники с площадью основания 100 м2, высотой 3м. На покрытие какой формы парника пойдёт меньше плёнки? В форме: 1) прямоугольного параллелепипеда, со сторонами оснований 5м и 20м, высотой 3м; 2)правильной четырёхугольной призмы; 3)пирамиды с прямоугольным основанием, стороны которого 5м и 20м. 4)цилиндра; 5)прямоугольника со сторонами 6м и 16,7 м, накрытого полуцилиндром. 6)конуса; 7)правильной четырёхугольной пирамиды;